Decimals on number lines
Topic Notes
In this lesson, we will learn:
- How to read number lines for decimals to the tenths or hundredths
- How to draw a point to represent a decimal on a decimal number line
Notes:
- A number line is a picture of a straight line with vertical markings of equal spacing
- Number lines increase from left to right (small big)
- Decimals are numbers with place values even smaller than the ones place.
- Number lines can be divided even further between each number
- Splitting each division into 10 equal parts creates the next decimal place value
- Dividing the space between 0 to 1 into 10 equal parts, each part is a tenth
- Dividing the space between 0 to 0.1 into 10 equal parts, each part is a hundredth
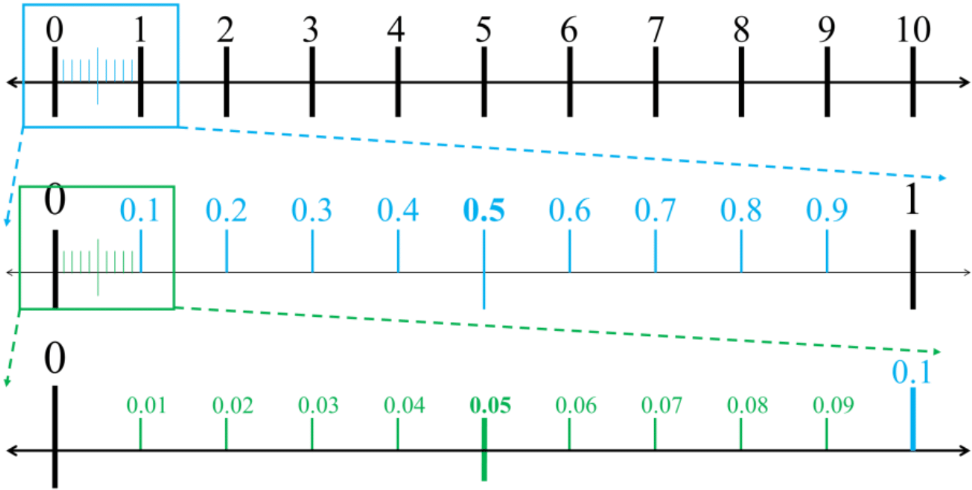
- From 0 to 1, it is first split into 10 equal parts (tenths = 0.1)
- Each of these tenths 0.1 will be split into 10 more equal parts (10 tenths each into 10 parts = 10 × 10 = 100 parts)
- Ultimately, the space between 0 and 1 will be split into 100 equal parts
- That's why each 0.01 is called a hundredth (one of the 100 parts)
Introduction
Decimals on number lines are a fundamental concept in mathematics, bridging the gap between whole numbers and fractions. Our lesson begins with an essential introduction video that lays the groundwork for understanding this crucial topic. This video serves as a visual guide, making abstract concepts more tangible and easier to grasp. As we delve deeper, we'll explore how to read number lines featuring decimals to the tenths and hundredths, providing you with the skills to accurately interpret these mathematical representations. Additionally, we'll learn the art of drawing points to represent decimals on a number line, a skill that reinforces spatial understanding and numerical relationships. By mastering these concepts, you'll gain a solid foundation for more advanced mathematical topics and real-world applications. Whether you're a student or simply curious about mathematics, this lesson will equip you with valuable knowledge about decimals and their representation on number lines.
Understanding Number Lines
A number line is a fundamental mathematical tool that visually represents numbers in a linear sequence. It consists of a straight horizontal line with vertical markings placed at equal intervals along its length. These vertical markings, often called tick marks, represent specific numerical values and are crucial for understanding the concept of numerical order and magnitude.
One of the key features of a number line is that numbers increase from left to right. This consistent progression allows us to easily compare and order numbers. As you move to the right along the line, the numbers become larger, while moving to the left leads to smaller numbers. This left-to-right increase is a universal convention that helps maintain clarity and consistency in mathematical representations.
The equal spacing between the vertical markings on a number line is essential for accurately representing numerical relationships. Each interval between two consecutive markings typically represents a consistent numerical increment, such as 1, 5, or 10, depending on the scale of the number line. This uniform spacing helps visualize the relative distances between numbers and supports concepts like addition, subtraction, and measurement.
To illustrate these principles, let's consider a basic number line:
In this example, we can see a simple number line ranging from 0 to 10. Each vertical marking represents a whole number, with equal spacing between them. To read a whole number on this number line, we simply need to identify the point that aligns with a specific vertical marking.
For instance, let's focus on the point representing the number 6. To locate this number, we start at 0 and count the vertical markings to the right until we reach the sixth mark. This point precisely indicates the position of 6 on the number line. Understanding how to read and interpret these points is crucial for various mathematical operations and concepts.
Number lines are versatile tools that can be extended to represent fractions, decimals, and even negative numbers. They serve as a visual aid for understanding numerical relationships, performing calculations, and grasping more complex mathematical concepts. By mastering the basics of number lines, students build a strong foundation for future mathematical learning and problem-solving skills.
Introducing Decimals on Number Lines
Decimals play a crucial role in our number system, allowing us to represent values between whole numbers with precision. Understanding how decimals fit into number lines is essential for grasping their true nature and significance. Let's explore how these fractional parts of numbers find their place on the familiar number line we use for whole numbers.
To begin, imagine a standard number line with whole numbers marked at regular intervals. Between any two consecutive whole numbers, there exists an infinite number of points, each representing a unique decimal value. These points correspond to numbers that are not whole but contain fractional parts smaller than one.
The concept of place values is fundamental to understanding decimals. While whole numbers use place values to the left of the ones place (tens, hundreds, thousands, etc.), decimals introduce place values to the right of the ones place. These new place values represent parts smaller than one whole unit.
The first place value to the right of the decimal point is called the tenths place. It represents fractions of one-tenth of a whole unit. Moving further right, we encounter the hundredths place, which represents one-hundredth of a whole unit. This pattern continues with thousandths, ten-thousandths, and so on, each place value representing a smaller fraction of the whole.
To visualize how decimals fit onto a number line, let's focus on the space between two whole numbers, such as 1 and 2. This interval can be divided into ten equal parts to represent tenths. Each of these parts represents a decimal increment of 0.1. So, moving from left to right, we would see points for 1.1, 1.2, 1.3, and so on, up to 1.9 before reaching 2.
But we can go even further. Each of these tenths can be subdivided into ten more parts to represent hundredths. This finer division allows us to pinpoint locations for numbers like 1.15, 1.23, or 1.78 on the number line. The process of subdivision can continue indefinitely, allowing for increasingly precise decimal representations.
For example, let's consider the point that represents 1.5 on the number line. This point would be exactly halfway between 1 and 2. It's equivalent to one and five-tenths or one and a half. Moving slightly to the right, we might find 1.52, which is one whole, five-tenths, and two-hundredths.
Understanding decimals on a number line helps us grasp their relative sizes and relationships. We can see that 1.7 is closer to 2 than it is to 1, or that 1.03 is just a tiny step away from 1. This visual representation reinforces the concept that decimals are simply a way of expressing parts of whole numbers with great precision.
As we become more comfortable with decimals on the number line, we start to see how they bridge the gaps between whole numbers, providing a continuous spectrum of values. This continuity is essential in many real-world applications, from precise measurements in science and engineering to financial calculations in economics and business.
In conclusion, decimals find their place on number lines by occupying the spaces between whole numbers, representing fractional parts with increasing precision as we move to smaller place values. By dividing the intervals between whole numbers into tenths, hundredths, and beyond, we can locate any decimal value with pinpoint accuracy on the number line, enhancing our understanding of the number system and its practical applications in the world around us.
Representing Tenths on a Number Line
Understanding how to represent tenths on a number line is a fundamental skill in mathematics that helps build a strong foundation for working with decimals. To divide the space between whole numbers into 10 equal parts and represent tenths, we need to follow a systematic approach. This process not only enhances our understanding of fractions and decimals but also improves our ability to visualize and interpret numerical data.
Let's begin by considering the space between 0 and 1 on a number line. To represent tenths, we need to divide this space into 10 equal parts. Imagine drawing a straight line and marking 0 at the left end and 1 at the right end. Now, we need to create 9 evenly spaced marks between these two points. It's crucial to ensure that these marks are precisely spaced to maintain accuracy in our representation.
Once we have our 10 equal parts, we can start labeling each mark to represent tenths. We begin with 0.1 (one-tenth) at the first mark after 0, then 0.2 (two-tenths) at the second mark, and so on. This process continues until we reach 0.9 (nine-tenths) at the last mark before 1. It's important to note that 1.0 is equivalent to 1 because it represents ten-tenths, which is a whole unit.
The labeling process helps us visualize how tenths relate to whole numbers. Each tenth represents a fraction of the whole, with 0.1 being one-tenth of the way from 0 to 1, 0.2 being two-tenths of the way, and so forth. This visual representation makes it easier to understand the relative size and position of decimal numbers.
Emphasizing equal spacing between each mark is crucial for accurate representation. If the spaces are not equal, it can lead to misinterpretation of the values and their relationships. Precise markings ensure that each tenth is given its proper place on the number line, allowing for correct comparisons and calculations.
When working with tenths on a number line, it's helpful to use tools like rulers or graph paper to maintain consistency in spacing. These tools can assist in creating evenly distributed marks and ensure accuracy in representation. Additionally, using different colors for whole numbers and tenths can help distinguish between them visually, making the number line easier to read and interpret.
Understanding how to represent tenths on a number line is not just about mathematical accuracy; it also develops spatial reasoning skills. By visualizing the relationship between whole numbers and their fractional parts, students can better grasp concepts like ordering decimals, comparing fractions, and even basic arithmetic operations involving decimals.
This skill of dividing space into equal parts and representing tenths extends beyond the 0 to 1 range. The same principle can be applied between any two consecutive whole numbers on a number line. For example, the space between 3 and 4 can be divided into tenths in the same way, with 3.1, 3.2, 3.3, and so on, up to 3.9.
As students become more comfortable with representing tenths, they can progress to more complex decimal representations, such as hundredths or thousandths. The foundational understanding of dividing space into equal parts remains the same, but the precision and detail increase.
In practical applications, understanding tenths and their representation on a number line is invaluable. It's used in various fields, from measuring ingredients in cooking to precise measurements in scientific experiments. This skill also forms the basis for more advanced mathematical concepts, including percentages, ratios, and even basic algebra.
To reinforce this concept, educators often use hands-on activities. For instance, students might create their own number lines using string and beads, with each bead representing a tenth. This tactile approach helps solidify the understanding of equal spacing and the relationship between tenths and whole numbers.
In conclusion, representing tenths on a number line by dividing the space between whole numbers into 10 equal parts is a crucial mathematical skill. It requires precision in marking equal spaces, careful labeling from 0.1 to 0.9, and understanding that 1.0 is equivalent to 1. This process not only
Representing Hundredths on a Number Line
Understanding hundredths on a number line is a crucial step in mastering decimal representation. To visualize hundredths, we need to further divide the space between tenths into 10 equal parts. This process results in 100 equal parts between whole numbers, allowing for a more precise representation of decimal values.
Let's start by examining the space between 0 and 1 on a number line. We've already learned that this space can be divided into 10 equal parts to represent tenths. Now, we'll take each of these tenth intervals and divide them again into 10 smaller, equal parts. This subdivision creates hundredths.
Imagine zooming in on the first tenth of the number line, the space between 0 and 0.1. Within this small segment, we can now see 10 tiny, equal divisions. These represent hundredths, ranging from 0.01 to 0.09. Each of these marks indicates a hundredth of the whole unit.
The labeling of hundredths follows a logical pattern. Starting from the beginning of the first tenth, we have:
- 0.01 (one-hundredth)
- 0.02 (two-hundredths)
- 0.03 (three-hundredths)
- 0.04 (four-hundredths)
- 0.05 (five-hundredths)
- 0.06 (six-hundredths)
- 0.07 (seven-hundredths)
- 0.08 (eight-hundredths)
- 0.09 (nine-hundredths)
The tenth mark in this sequence would be 0.10, which is equivalent to one-tenth and marks the beginning of the next tenth interval.
It's important to understand the relationship between tenths and hundredths. Each tenth is made up of 10 hundredths. For example, 0.1 (one-tenth) is the same as 0.10 (ten-hundredths). This relationship extends throughout the number line:
- 0.2 is equivalent to 0.20 (twenty-hundredths)
- 0.3 is equivalent to 0.30 (thirty-hundredths)
- 0.4 is equivalent to 0.40 (forty-hundredths)
- And so on...
By dividing each tenth into 10 equal parts, we create a total of 100 equal parts between whole numbers. This allows for precise representation of small quantities and measurements. For instance, we can now accurately place numbers like 0.37 (thirty-seven hundredths) or 0.82 (eighty-two hundredths) on the number line.
Understanding hundredths is essential in many real-world applications. For example, in finance, we often deal with currency values to the nearest cent (hundredth of a dollar). In sports, race times are frequently measured to the hundredth of a second. Even in everyday measurements, like temperature readings, hundredths can provide a level of precision that's sometimes necessary.
As you practice working with hundredths on a number line, remember these key points:
- There are 100 equal parts between whole numbers when representing hundredths.
- Each tenth is divided into 10 equal parts to create hundredths.
- Hundredths are labeled from 0.01 to 0.09 within each tenth.
- The relationship between tenths and hundredths is crucial for understanding decimal place value.
By mastering the concept of hundredths on a number line, you're building a strong foundation for working with decimals and fractions. This understanding will prove invaluable as you progress to more advanced mathematical concepts
Reading and Plotting Decimals on Number Lines
Understanding how to read and plot decimal values on a number line is a crucial skill in mathematics. This guide will walk you through the process step-by-step, focusing on reading tenths and hundredths, and provide practice exercises to reinforce your learning.
Reading Decimals on a Number Line
- Identify the whole numbers on the number line.
- Determine the intervals between whole numbers.
- For tenths, divide the space between whole numbers into 10 equal parts.
- For hundredths, divide each tenth into 10 equal parts.
Example: Reading Tenths
On a number line from 0 to 1, each tenth is represented by a small tick mark. 0.1 is the first mark after 0, 0.2 is the second, and so on.
Example: Reading Hundredths
Between 0.1 and 0.2, there are 10 smaller divisions. These represent hundredths. 0.11 is the first mark after 0.1, 0.12 is the second, and so on.
Plotting Decimals on a Number Line
- Identify the whole numbers that your decimal falls between.
- Determine how many tenths and hundredths the decimal represents.
- Count the appropriate number of tick marks from the lower whole number.
- Mark the point precisely on the number line.
Precision is crucial when plotting decimals. Always use a ruler or straightedge to ensure accurate placement. Remember that small errors in placement can lead to significant misinterpretations of the value.
Practice Exercises
To reinforce your understanding of reading and plotting decimals on number lines, try these exercises:
- Identify the following points on a number line from 0 to 1: 0.3, 0.7, 0.9
- Plot these decimals on a number line from 1 to 2: 1.25, 1.6, 1.95
- On a number line from 2 to 3, mark and label: 2.15, 2.48, 2.73, 2.91
- Create a number line from 3 to 4 and plot: 3.07, 3.32, 3.65, 3.89
As you practice, focus on accuracy and precision. Start by estimating where the decimal should be placed, then use the tick marks to fine-tune your placement. Remember that reading decimals on a number line is about understanding proportions and intervals between whole numbers.
By mastering the skill of reading and plotting decimals on number lines, you'll develop a stronger intuition for decimal values and their relationships to whole numbers. This foundational skill will prove invaluable as you progress to more advanced mathematical concepts involving decimals, fractions, and proportions.
Continue practicing with various ranges and decimal values to improve your proficiency. As you become more comfortable, challenge yourself with more complex decimals and larger number line ranges. With consistent practice, you'll find that reading and plotting decimals becomes second nature, enhancing your overall mathematical abilities.
Conclusion
In this lesson, we explored the crucial concept of decimals on number lines, a fundamental skill in mathematics. The introduction video provided a solid foundation for understanding these concepts, emphasizing their importance in real-world applications. We learned how to accurately read and plot decimals on number lines, recognizing the significance of place value and scale. This knowledge is essential for more advanced mathematical topics and everyday problem-solving. To reinforce your learning, practice regularly by creating your own number lines and plotting various decimals. Consider exploring related topics such as fractions on number lines or comparing decimals using number lines. Remember, mastering decimals on number lines enhances your overall numerical literacy and problem-solving abilities. For further learning, investigate decimal operations, conversion between fractions and decimals, and applications in measurement and data analysis. By building on these skills, you'll develop a stronger mathematical foundation for future studies and real-life situations.
Introduction to Decimals on Number Lines:
How to create decimal number lines for decimal tenths and decimal hundredths
Step 1: Understanding the Basic Number Line
In this lesson, we'll be talking about decimals on number lines. First of all, let's review what a number line looks like. A number line is a straight line with arrows on both sides, indicating that it extends infinitely in both directions. It is marked with numbers in a continuum, meaning the numbers are in order and increase from left to right. Smaller values are on the left side, and as you move to the right, the values get bigger. For example, a number line might count from 0 to 10 in increments of 1.
Step 2: Identifying Points on the Number Line
If we have a point on the number line, such as a little circle drawn in yellow, we need to determine what number it represents. For instance, if the point is exactly on the marking of 6, it represents the number 6. This is how we read the number line: by seeing where the point is located and identifying the corresponding marking.
Step 3: Introducing Decimals on the Number Line
Now, let's talk about decimals on a number line. Unlike whole numbers, decimals can be found between the markings of whole numbers. For example, a point between the increments of 1 and 2 is more than 1 but not enough to be 2. This is where decimal increments come into play. We need to figure out how to label these points and give them a value on the number line.
Step 4: Creating Decimal Number Lines for Tenths
To create a decimal number line for tenths, we need to divide the space between each whole number into 10 equal parts. For example, the space between 0 and 1 will be split into 10 equal divisions. Each division represents one-tenth (0.1). So, the markings will be 0.1, 0.2, 0.3, and so on, up to 1.0. The fifth marking, 0.5, is exactly halfway between 0 and 1.
Step 5: Zooming In for Clarity
To make the divisions clearer, we can zoom in on the space between 0 and 1. By stretching this section, we can see the 10 equal parts more clearly. Each part is worth one-tenth (0.1). The first marking is 0.1, the second is 0.2, and so on, up to 1.0. This process helps us understand how to create and read decimal number lines for tenths.
Step 6: Creating Decimal Number Lines for Hundredths
To create a decimal number line for hundredths, we need to divide the space between each tenth into 10 equal parts. For example, the space between 0 and 0.1 will be split into 10 equal divisions. Each division represents one-hundredth (0.01). So, the markings will be 0.01, 0.02, 0.03, and so on, up to 0.1. The fifth marking, 0.05, is exactly halfway between 0 and 0.1.
Step 7: Zooming In for Clarity on Hundredths
To make the divisions clearer, we can zoom in on the space between 0 and 0.1. By stretching this section, we can see the 10 equal parts more clearly. Each part is worth one-hundredth (0.01). The first marking is 0.01, the second is 0.02, and so on, up to 0.1. This process helps us understand how to create and read decimal number lines for hundredths.
Step 8: Summary
In summary, creating decimal number lines involves dividing the space between whole numbers into smaller, equal parts. For tenths, we divide the space into 10 equal parts, and for hundredths, we divide each tenth into 10 equal parts. This allows us to accurately represent and read decimal values on a number line.
FAQs
-
What is a number line and how does it relate to decimals?
A number line is a visual representation of numbers in order. For decimals, it allows us to show fractional parts between whole numbers. The space between two whole numbers can be divided into tenths and hundredths, enabling precise placement of decimal values.
-
How do you represent tenths on a number line?
To represent tenths, divide the space between two whole numbers into 10 equal parts. Each part represents one-tenth (0.1). For example, between 0 and 1, you would have marks at 0.1, 0.2, 0.3, and so on up to 0.9.
-
What's the difference between representing tenths and hundredths on a number line?
While tenths divide the space between whole numbers into 10 parts, hundredths further divide each tenth into 10 smaller parts, resulting in 100 total divisions between whole numbers. This allows for more precise representation of decimal values like 0.23 or 0.78.
-
How can I accurately plot a decimal on a number line?
To plot a decimal, first identify the whole numbers it falls between. Then, count the appropriate number of tenths and hundredths from the lower whole number. Use a ruler for precision. For example, to plot 3.45, start at 3, move 4 tenths to the right, then 5 hundredths further.
-
Why is understanding decimals on number lines important?
Understanding decimals on number lines is crucial for developing number sense, comparing decimal values, and visualizing mathematical operations. It forms a foundation for more advanced concepts in algebra, measurement, and data analysis, and has practical applications in fields like finance, science, and engineering.
Prerequisite Topics
Understanding decimals on number lines is a crucial skill in mathematics, building upon several fundamental concepts. While there are no specific prerequisite topics provided for this subject, it's important to recognize that a strong foundation in basic number sense and number line comprehension is essential. These underlying skills form the bedrock for grasping more complex ideas like decimals on number lines.
To fully appreciate decimals on number lines, students should be comfortable with whole numbers and their representation on a number line. This includes understanding the concept of intervals, the idea that numbers increase from left to right, and the ability to identify and place whole numbers accurately. Additionally, familiarity with fractions can be beneficial, as decimals are essentially another way to express fractional parts.
A solid grasp of place value is also crucial when working with decimals. Students need to understand how the position of a digit affects its value, both to the left and right of the decimal point. This knowledge helps in accurately placing and reading decimals on a number line, as it allows for precise interpretation of the intervals between whole numbers.
Moreover, basic arithmetic skills, particularly with whole numbers, provide a necessary foundation. The ability to perform addition, subtraction, multiplication, and division with whole numbers can greatly aid in understanding how decimals behave on a number line. These operations help in calculating distances between points and in estimating the position of decimals relative to whole numbers.
Understanding the concept of magnitude is another important aspect. Students should be able to compare and order whole numbers, which naturally extends to comparing and ordering decimals. This skill is crucial when placing decimals in their correct positions on a number line, especially when dealing with closely spaced values.
Lastly, a general familiarity with measurement concepts can be helpful. Many real-world applications of decimals on number lines involve measurements, such as length, weight, or temperature. Having a practical understanding of these concepts can make the abstract idea of decimals on a number line more tangible and relatable.
While these prerequisite skills are not explicitly listed, they form the essential groundwork for understanding decimals on number lines. By ensuring a strong foundation in these areas, students can approach the topic with confidence, ready to build upon their existing knowledge and tackle more advanced concepts in mathematics.

