Compare and order decimals
Notas del Tema
In this lesson, we will learn:
- How to compare the value of two decimal numbers
- How to order a list of decimals in ascending and descending order
Notes:
- To compare two decimal numbers, we want to know how big or small the values are
- We use these symbols to compare numbers:

- We can compare using number lines:

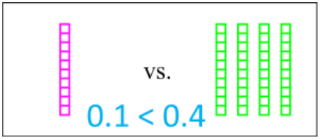
- We can also compare using base ten (block) models:
- The steps for comparing two numbers:
- Start with the biggest (left) place value.
- Is the digit in this place value different between the two numbers?
- YES: compare the digit (0 = smallest, 9 = biggest).
- NO: move to the next smaller place value (right) and repeat step 2.
- If all digits are the same in both numbers, they are equal.
- Once you have found a difference for a place value, it does not matter what numbers are in the places further on the right (smaller places)
- i.e. recall equivalent decimal tenths and hundredths 0.8=0.80
- ex. 8.9 > 8.79 (more decimal place values does not necessarily make the value greater)
- There are two ways to order a list of decimals:
- Ascending order: which means from least to greatest
- increasing; smallest to biggest (ex. 1.1 < 1.2 < 1.3 < 1.4)
- Descending order: which means from greatest to least
- decreasing; biggest to smallest (ex. 1.4 > 1.3 > 1.2 > 1.1)
Introduction
Welcome to our lesson on comparing and ordering decimals, a fundamental skill in mathematics. We'll begin with an introduction video that provides a crucial foundation for understanding these concepts. This video will help you grasp the basics of decimal comparison and ordering, setting the stage for more in-depth learning. Throughout this lesson, we'll explore how to compare the value of two decimal numbers, a skill essential for various mathematical operations and real-world applications. You'll learn to determine which decimal is greater or lesser, and why. Additionally, we'll cover techniques for ordering a list of decimals in both ascending and descending order. This skill is particularly useful in data analysis, scientific measurements, and everyday situations involving money or measurements. By mastering these concepts, you'll enhance your overall mathematical proficiency and problem-solving abilities. Let's dive in and discover the fascinating world of decimal comparison and ordering!
Understanding Decimal Comparison
Comparing decimals is an essential skill in mathematics, and visual aids like number lines and base ten block models can greatly enhance our understanding of this concept. These tools help us determine which decimal is greater or smaller by providing a concrete representation of abstract numerical values. Let's explore how we can use these visual aids to compare decimals effectively.
Number lines are particularly useful for comparing decimals. To use a number line, we first need to identify the range of values we're working with. For example, when comparing 0.1 and 0.4, we would focus on the range between 0 and 1. We then mark these decimals on the number line, with 0.1 being closer to 0 and 0.4 being closer to the middle. By visually representing these values, we can easily see that 0.4 is further to the right on the number line, indicating that it is greater than 0.1.
Base ten block models offer another effective way to compare decimals. These models use different sized blocks to represent whole numbers and decimal fractions. For our example of 0.1 and 0.4, we would use tenth blocks. One tenth block would represent 0.1, while four tenth blocks would represent 0.4. By physically placing these blocks side by side, we can visually confirm that 0.4 is indeed greater than 0.1, as it takes up more space.
When comparing decimals, it's crucial to understand that we're determining how big or small the values are in relation to each other. Using our example, we can say that 0.4 is greater than 0.1 because it represents a larger portion of a whole unit. Conversely, 0.1 is less than 0.4 because it represents a smaller fraction of the whole.
These visual aids are particularly helpful when dealing with decimals that aren't as easily comparable at first glance. For instance, when comparing 0.25 and 0.3, using a number line or base ten blocks can quickly show that 0.3 is greater, even though 25 is larger than 3 in whole numbers.
It's important to note that when using number lines for decimal comparison, we need to pay close attention to the scale. The space between 0 and 0.1 on a number line is the same as the space between 0.1 and 0.2, 0.2 and 0.3, and so on. This consistent spacing helps us accurately place and compare decimal values.
Similarly, when using base ten block models, we must ensure that we're using the appropriate sized blocks for the decimals we're comparing. Tenths, hundredths, and thousandths are represented by progressively smaller blocks, allowing us to make precise comparisons between decimals with different place values.
By utilizing these visual aids, students can develop a strong intuitive understanding of decimal values and their relationships. This foundation is crucial for more advanced mathematical concepts and real-world applications where decimal comparisons are frequently used, such as in finance, science, and engineering.
In conclusion, comparing decimals using number lines and base ten block models provides a tangible way to understand the relative size of decimal values. These visual representations help clarify the concept of "greater than" and "less than" when dealing with fractions of whole numbers. By practicing with these tools, students can build confidence in their ability to compare and order decimals accurately, setting the stage for success in more complex mathematical operations involving decimal numbers.
Comparison Symbols and Techniques
When it comes to comparing numbers, three essential symbols play a crucial role: less than (<), greater than (>), and equal to (=). These comparison symbols are fundamental tools in mathematics, allowing us to express relationships between different numerical values quickly and efficiently.
Let's start with the less than (<) and greater than (>) symbols. A helpful memory aid for distinguishing between these two is the 'alligator mouth' trick. Imagine the symbol as an alligator's open mouth, always eager to eat the larger number. The alligator will face the bigger value, with its mouth open wide to gobble it up. For example, in the expression 5 < 8, the alligator's mouth (the wider part of the symbol) points towards 8, the larger number.
The equal to (=) symbol is straightforward, indicating that the values on both sides are identical. For instance, 7 = 7 shows that both sides have the same value.
Now, let's explore how to use these comparison symbols with whole numbers and decimals. For whole numbers, the process is relatively simple. Compare the digits from left to right until you find a difference. For example, when comparing 352 and 348:
1. Compare the hundreds place: 3 = 3 (move to the next digit)
2. Compare the tens place: 5 > 4
3. We can stop here, as 352 > 348
Comparing decimals requires a bit more attention to detail. The key is to align the decimal points and then compare digits from left to right, starting with the whole number part. Let's compare 3.14 and 3.2:
1. Align the decimal points: 3.14 and 3.20 (adding a zero doesn't change the value)
2. Compare the whole number part: 3 = 3 (move to the next digit)
3. Compare the tenths place: 1 < 2
4. We can stop here, as 3.14 < 3.2
The step-by-step process for comparing digits in decimal numbers, starting from the leftmost place value, is as follows:
1. Align the decimal points of the numbers being compared.
2. Start with the leftmost digit (the largest place value).
3. Compare the digits in this place value:
- If one digit is larger, that number is greater.
- If the digits are equal, move to the next place value to the right.
4. Repeat step 3 until you find a difference or reach the end of both numbers.
5. If you reach the end and all digits are equal, the numbers are equal.
This method works because place value determines a digit's significance. The leftmost digits have the greatest impact on a number's overall value. By comparing from left to right, we ensure that we're always evaluating the most significant differences first.
Remember, when comparing negative numbers, the rules change slightly. The number closer to zero on the number line is considered greater. For example, -2 > -5, because -2 is closer to zero on the number line.
Mastering these comparison symbols and techniques is essential for various mathematical operations and real-world applications. Whether you're analyzing data, solving equations, or making everyday decisions involving numbers, understanding how to compare values accurately is a fundamental skill. Practice using the 'alligator mouth' trick and the step-by-step comparison process to build confidence in your ability to compare numbers of all types.
Comparing Decimals with Different Place Values
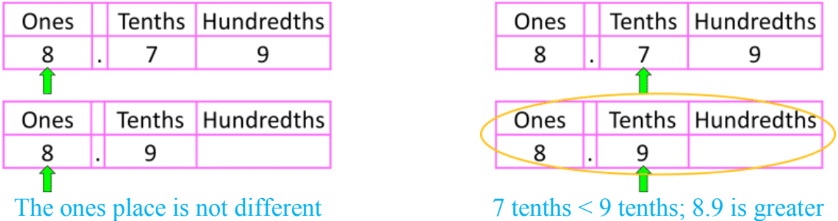
Comparing decimals with different numbers of decimal places can be tricky, but it's an essential skill in mathematics. Let's explore how to compare decimals like 8.79 and 8.9 accurately, addressing common misconceptions and highlighting key concepts.
The first step in comparing decimals with different decimal places is to align their place values correctly. This is crucial because it allows us to compare like terms. In our example of 8.79 and 8.9, we need to align the tenths place (the first digit after the decimal point) for both numbers.
To achieve this alignment, we can use trailing zeros. Trailing zeros are zeros added to the right of a decimal number without changing its value. In this case, we can add a trailing zero to 8.9, making it 8.90. Now, we have:
8.79
8.90
With the place values aligned, we can easily compare the numbers digit by digit, starting from the left. Both numbers have 8 in the ones place, so we move to the tenths place. Here, 9 is greater than 7, so we can conclude that 8.90 (or 8.9) is greater than 8.79.
It's important to address a common misconception: thinking that 79 hundredths is larger than 9 tenths because 79 is a bigger number than 9. This error occurs when students focus on the whole numbers after the decimal point without considering their place values. In reality, 9 tenths (0.9) is larger than 79 hundredths (0.79) because tenths have a greater value than hundredths.
To further illustrate this concept, let's look at another example. Compare 3.4 and 3.35:
3.4
3.35
By adding a trailing zero to 3.4, we get:
3.40
3.35
Now it's clear that 3.40 is greater than 3.35.
When comparing decimals, it's crucial to remember that each place value to the right of the decimal point represents a smaller fraction. Tenths are larger than hundredths, which are larger than thousandths, and so on. This understanding helps avoid the misconception that more decimal places automatically mean a larger number.
Practice is key to mastering decimal comparison. Try comparing various pairs of decimals with different numbers of decimal places, always remembering to align place values and use trailing zeros when necessary. With time and practice, comparing decimals will become second nature, providing a solid foundation for more advanced mathematical concepts.
In conclusion, comparing decimals with different numbers of decimal places involves careful attention to place value alignment and the strategic use of trailing zeros. By understanding these principles and avoiding common misconceptions, students can confidently and accurately compare decimal numbers, regardless of their varying decimal places.
Ordering Decimals
Understanding how to arrange decimals in ascending and descending order is a crucial skill in mathematics. Ascending order refers to arranging numbers from the smallest to the largest (least to greatest), while descending order means arranging numbers from the largest to the smallest (greatest to least). This concept applies to whole numbers, decimals, and mixed numbers.
To arrange decimals in ascending order (least to greatest), follow these steps:
- Line up the decimal points vertically.
- Compare the digits in each place value, starting from the left.
- If the digits are the same, move to the next place value to the right.
- Continue until you find a difference or reach the end of the number.
- Arrange the numbers based on these comparisons.
For descending order (greatest to least), follow the same steps but arrange the numbers from largest to smallest.
Let's look at an example with mixed whole numbers and decimals:
Arrange in ascending order: 3.14, 0.9, 3.04, 10.2, 3.140
- Line up the decimal points:
3.140
0.900
3.040
10.200
3.140 - Compare digits from left to right:
10.200 is the largest (starts with 10)
3.140 and 3.140 are equal
3.040 is next
0.900 is the smallest - Final ascending order: 0.9, 3.04, 3.14, 3.140, 10.2
For descending order, we would reverse this list: 10.2, 3.140, 3.14, 3.04, 0.9
Remember, when comparing decimals with different numbers of decimal places, you can add zeros to the right of the last digit to make them easier to compare. This doesn't change the value of the number.
Practice is key to mastering this skill. Try arranging different sets of decimals and mixed numbers in both ascending and descending order to improve your understanding and speed. This ability is essential for various mathematical operations and real-world applications, such as analyzing data, comparing measurements, or working with financial figures.
Practice Problems and Applications
Let's dive into some practice problems to sharpen your skills in comparing and ordering decimals. These exercises will not only test your understanding but also demonstrate how these concepts apply in real-world scenarios.
Problem Set 1: Comparing Prices
1. Sarah is comparing prices for a new laptop. She finds the following options:
- Store A: $799.99
- Store B: $800.05
- Store C: $799.95
Order these prices from least to greatest.
Solution: First, let's align the decimal points:
799.99
800.05
799.95
Comparing digit by digit, we can order them as: $799.95 < $799.99 < $800.05
Problem Set 2: Measuring Ingredients
2. A recipe calls for the following amounts of flour:
- 2.25 cups
- 2.5 cups
- 2.125 cups
Which measurement is the largest?
Try solving this one on your own before checking the solution!
Problem Set 3: Athletic Performance
3. In a 100-meter sprint, three athletes finished with these times:
- Athlete A: 10.08 seconds
- Athlete B: 10.1 seconds
- Athlete C: 10.09 seconds
Rank the athletes from fastest to slowest.
Solution: Remember, in racing, a lower time is better. Let's compare:
10.08
10.10 (10.1 is the same as 10.10)
10.09
Ranking from fastest to slowest: Athlete A (10.08s), Athlete C (10.09s), Athlete B (10.1s)
Independent Practice
Now, try these problems on your own:
4. Compare these gas prices: $3.459, $3.45, $3.461. Which station has the cheapest gas?
5. Order these heights from tallest to shortest: 5.75 feet, 5.8 feet, 5.725 feet.
6. A factory produces bolts with these diameters: 0.375 inches, 0.25 inches, 0.3 inches. Order them from thinnest to thickest.
Real-World Applications
Understanding how to compare and order decimals is crucial in many everyday situations:
- Shopping: Comparing prices to find the best deals
- Cooking: Measuring ingredients accurately
- Sports: Analyzing performance times and distances
- Construction: Ensuring precise measurements for materials
- Finance: Comparing interest rates or investment returns
By practicing these problems, you're developing skills that will help you make informed decisions in various aspects of life. Remember, when comparing decimals, always align the decimal points and compare digit by digit. If the whole numbers are the same, move to the tenths, then hundredths, and so on until you find a difference.
Keep practicing, and soon comparing and ordering decimals will become second nature!
Conclusion
In this lesson, we explored essential methods for comparing decimals, emphasizing the critical role of place value understanding. The introduction video served as a cornerstone, providing a visual foundation for grasping these concepts. Key points covered include aligning decimal points, comparing digits from left to right, and using place value charts. We learned that zeros can be added to the right of the last decimal place without changing the value, facilitating easier comparisons. The importance of precision in decimal comparisons, especially in real-world applications like finance and science, was highlighted. Students are encouraged to practice these skills regularly, using worksheets, online tools, and real-life scenarios to reinforce their understanding. For those seeking to deepen their knowledge, exploring additional resources on decimal operations and place value is recommended. Remember, mastering decimal comparisons is a fundamental skill that will prove invaluable in various academic and practical contexts.
Introduction to Comparing and Ordering Decimals: How to Compare Two Decimal Numbers
In this guide, we will walk you through the process of comparing two decimal numbers step by step. By the end of this guide, you will be able to determine which decimal is larger or smaller using various methods.
Step 1: Understanding the Concept of Decimal Comparison
When comparing and ordering decimals, the primary question we are asking is how big or small the decimal number is. This involves understanding the value of each decimal in relation to others. The first method to visualize this is by using a number line.
Step 2: Using a Number Line
A number line is a useful tool for comparing decimals. Let's consider a number line that ranges from 0 to 10, with increments of 1. On this number line, smaller numbers are positioned to the left, and larger numbers are positioned to the right. This principle holds true for any number line.
For decimals, we focus on the space between 0 and 1, dividing it into 10 equal parts, each representing a tenth. For example, 0.1, 0.2, 0.3, and so on. To compare two decimals, such as 0.1 and 0.4, we observe their positions on the number line. Since 0.1 is closer to the left, it is smaller, while 0.4, being further to the right, is larger.
Step 3: Using Base 10 Block Models
Another method to compare decimals is by using base 10 block models. These models visually represent the value of decimals. For instance, 0.1 can be represented by one stick of 10 small blocks, while 0.4 can be represented by four sticks of 10 small blocks each. By comparing the total number of blocks, we can see that 0.4, with 40 blocks, is greater than 0.1, which has only 10 blocks.
Step 4: Comparing Digits in Place Value Charts
We can also compare decimals by examining their digits in place value charts. For example, comparing 0.1 and 0.4 involves looking at the tenths place. Both numbers have zero in the ones place, but 0.1 has one-tenth, while 0.4 has four-tenths. Since four-tenths is greater than one-tenth, 0.4 is larger than 0.1.
Step 5: Using Comparison Symbols
When comparing decimals, we use specific symbols: less than (<), greater than (>), and equal to (=). To remember which symbol to use, think of the symbols as alligator mouths that always want to eat the bigger number. For example, in the comparison 3 < 5, the open side of the symbol faces the larger number, 5. Similarly, in 8 > 4, the open side faces 8, the larger number.
Step 6: Applying the Symbols to Decimals
Now that we understand how to use the comparison symbols, let's apply them to our example decimals, 0.1 and 0.4. Since 0.4 is larger, we use the less than symbol to write 0.1 < 0.4. This formally expresses the comparison in a mathematical sentence.
Conclusion
By following these steps, you can effectively compare and order decimal numbers. Whether using a number line, base 10 block models, place value charts, or comparison symbols, each method provides a clear way to determine which decimal is larger or smaller. Practice these methods to become proficient in comparing decimals.
FAQs
Here are some frequently asked questions about comparing and ordering decimals:
-
Q: How do you compare decimals with different numbers of decimal places?
A: To compare decimals with different numbers of decimal places, first align the decimal points vertically. Then, add zeros to the right of the shorter decimal to make the number of decimal places equal. Compare the digits from left to right until you find a difference. For example, to compare 0.8 and 0.75, write them as 0.80 and 0.75, then compare. -
Q: What's the easiest way to remember the "greater than" and "less than" symbols?
A: A helpful trick is to think of the symbol as an alligator's mouth. The alligator always wants to eat the bigger number, so the open side of the symbol points to the larger number. For example, 5 < 8 (the mouth opens towards 8, the larger number). -
Q: How do you order decimals from least to greatest?
A: To order decimals from least to greatest (ascending order), follow these steps: 1) Align the decimal points. 2) Compare the digits in each place value, starting from the left. 3) If digits are the same, move to the next place value. 4) Arrange the numbers based on these comparisons, starting with the smallest. -
Q: Can adding zeros after the last decimal place change the value of a number?
A: No, adding zeros after the last decimal place does not change the value of a number. For example, 3.4, 3.40, and 3.400 all represent the same value. These zeros are called trailing zeros and are often used to make comparing decimals easier. -
Q: Why is understanding decimal comparison important in real life?
A: Understanding decimal comparison is crucial in many real-life situations. It's used in financial decisions (comparing prices or interest rates), cooking (measuring ingredients), sports (comparing performance times), construction (precise measurements), and scientific research. This skill helps in making informed decisions and performing accurate calculations in various fields.
Prerequisite Topics
Understanding the foundation of mathematics is crucial when it comes to comparing and ordering decimals. While there are no specific prerequisite topics listed for this subject, it's important to recognize that mathematical concepts build upon one another. A solid grasp of basic arithmetic and place value is essential for mastering the skill of comparing and ordering decimals.
When working with decimals, students need to have a strong understanding of whole numbers and fractions. The concept of place value extends beyond whole numbers and into the decimal realm. Recognizing that each digit to the right of the decimal point represents a smaller fraction of a whole is fundamental to comparing and ordering decimals accurately.
Additionally, familiarity with number lines can greatly aid in visualizing the relative positions of decimals. This spatial understanding helps students intuitively grasp the order of decimals and their relationships to one another. The ability to convert between fractions and decimals is also beneficial, as it provides multiple perspectives on the same numerical value.
Moreover, proficiency in rounding numbers can be helpful when comparing decimals, especially when dealing with numbers that have different numbers of decimal places. Understanding how to round to the nearest tenth, hundredth, or thousandth can simplify the comparison process and provide a quick estimation of a decimal's value.
It's also worth noting that a solid foundation in basic arithmetic operations (addition, subtraction, multiplication, and division) with whole numbers translates directly to working with decimals. These operations are often used in the process of comparing and ordering decimals, particularly when the numbers are close in value and require more detailed analysis.
While not explicitly listed as prerequisites, skills such as reading and writing numbers in expanded form can significantly enhance a student's ability to compare and order decimals. This skill helps in breaking down the components of a decimal, making it easier to compare digit by digit.
Lastly, a general sense of number sense and estimation skills play a crucial role in working with decimals. Being able to quickly estimate the value of a decimal in relation to benchmark numbers (like 0, 0.5, and 1) can greatly speed up the process of ordering multiple decimals.
In conclusion, while there may not be a specific list of prerequisite topics for comparing and ordering decimals, a strong foundation in basic arithmetic, place value, and number sense is invaluable. These fundamental skills provide the necessary framework for students to confidently approach more complex decimal operations. As students progress in their mathematical journey, they'll find that these core concepts continue to be relevant and applicable across various mathematical domains.

