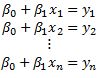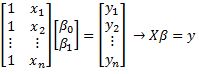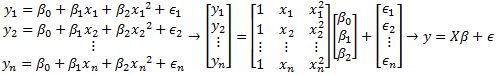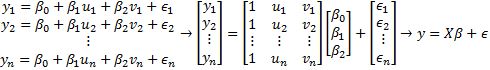Application to linear models
All in One PlaceEverything you need for JC, LC, and college level maths and science classes. | Learn with EaseWe’ve mastered the national curriculum so that you can revise with confidence. | Instant Help24/7 access to the best tips, walkthroughs, and practice exercises available. |
Make math click 🤔 and get better grades! 💯Join for Free
0/4
Intros
Lessons
- Applications to Linear Models Overview:
- Applying Least-Squares Problem to Economics
• Go from to
• → design matrix
• → parameter vector
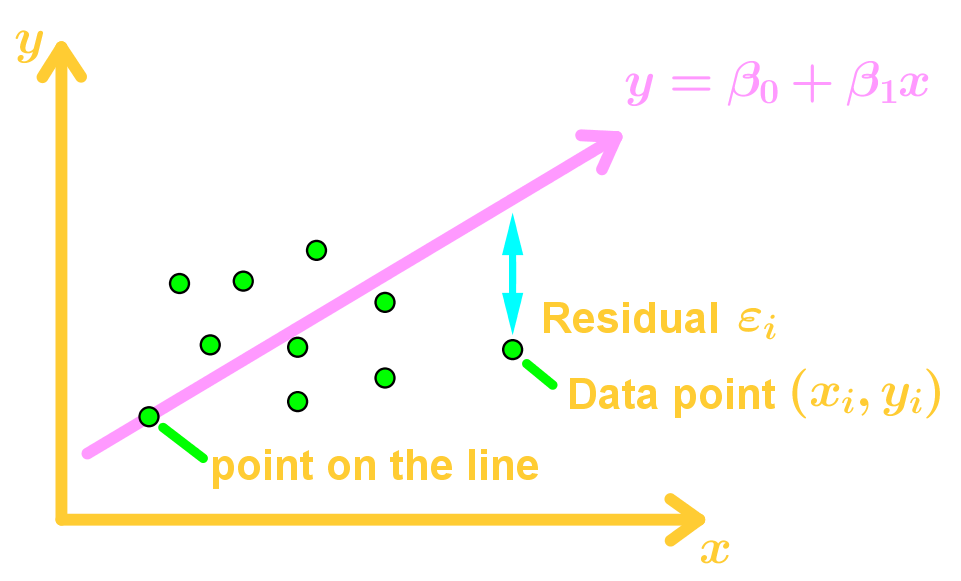
• → observation vector - Least-Squares Line
• Finding the best fit line
• Turning a system of equations into
• Using the normal equation
• Introduction of the residual vector - Least-Squares to Other Curves
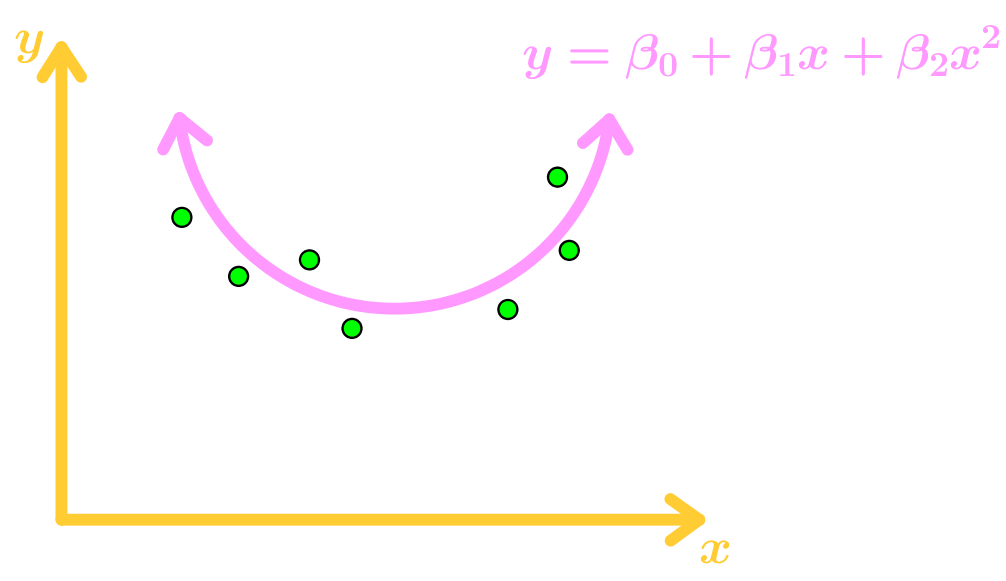
• Finding the Best Fit Curve (not a line)
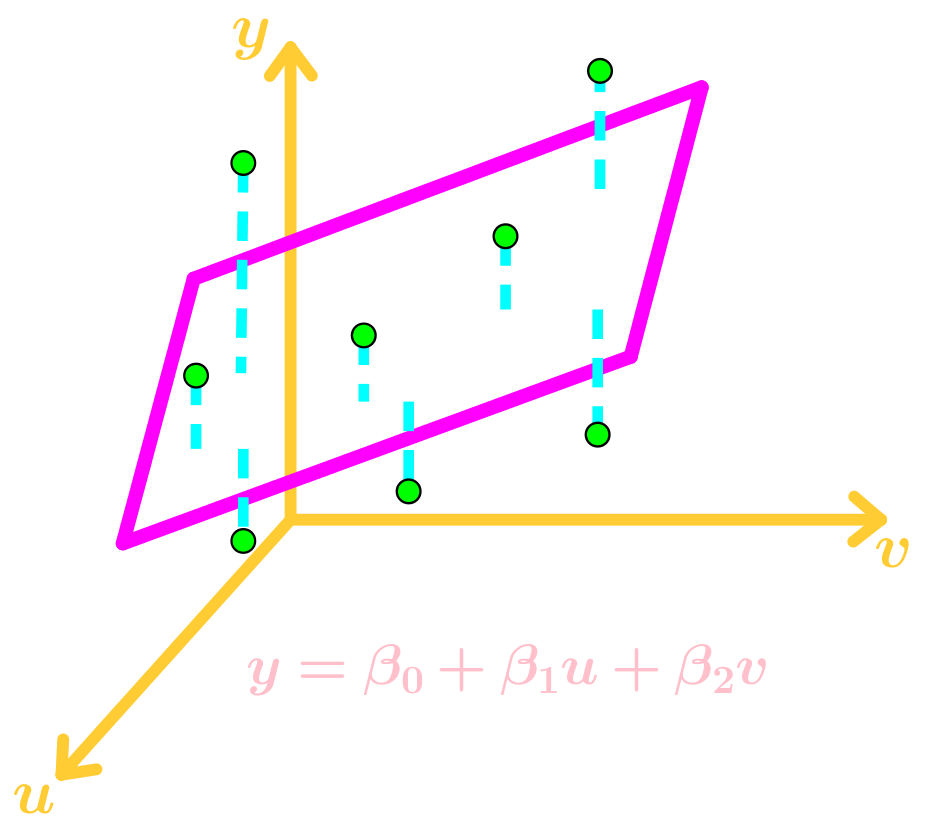
• Using the normal equation - Least-Squares to Multiple Regressions
• Multiple Regression → multivariable function
• Finding a Best Fit Plane
• Using the normal equation
0/5
Examples
Lessons
- Finding the Least-Squares Line
Find the equation of the least-squares line that best fits the given data points:
- Finding the Least-Squares of Other Curves
Suppose the monthly costs of a product depend on seasonal fluctuations. A curve that approximates the cost is
()
Suppose you want to find a better approximation in the future by evaluating the residual errors in each data point. Let's assume the errors for each data point to be .
Give the design matrix, parameter vector, and residual vector for the model that leads to a least-squares fit for the equation above. Assume the data are - An experiment gives the data points . Suppose we wish to approximate the data using the equation
First find the design matrix, observational vector, and unknown parameter vector. No need to find the residual vector. Then find the least-squares curve for the data. - Finding the Least Squares of Multiple Regressions
When examining a local model of terrain, we examine the data points to be and . Suppose we wish to approximate the data using the equation
First find the design matrix, observational vector, and unknown parameter vector. No need to find the residual vector. Then find the least-squares curve for the data. - Proof Question Relating to Linear Models
Show that