The matrix of a linear transformation
All in One PlaceEverything you need for JC, LC, and college level maths and science classes. | Learn with EaseWe’ve mastered the national curriculum so that you can revise with confidence. | Instant Help24/7 access to the best tips, walkthroughs, and practice exercises available. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Lessons
- The Matrix of a Linear Transformation Overview:
- The Standard Basis and Matrix
• T(x)=Ax,A: The Standard Matrix
• R2 standard Basis: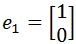 and
and 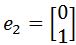
• R3 standard Basis: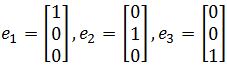
• Transformed standard basis
• Finding the Standard Matrix - Finding the Standard Matrix Geometrically in R2
• Drawing the Standard basis on a Graph
• Identifying the Transformed Standard Basis
• Combining the Standard Basis' into a Matrix
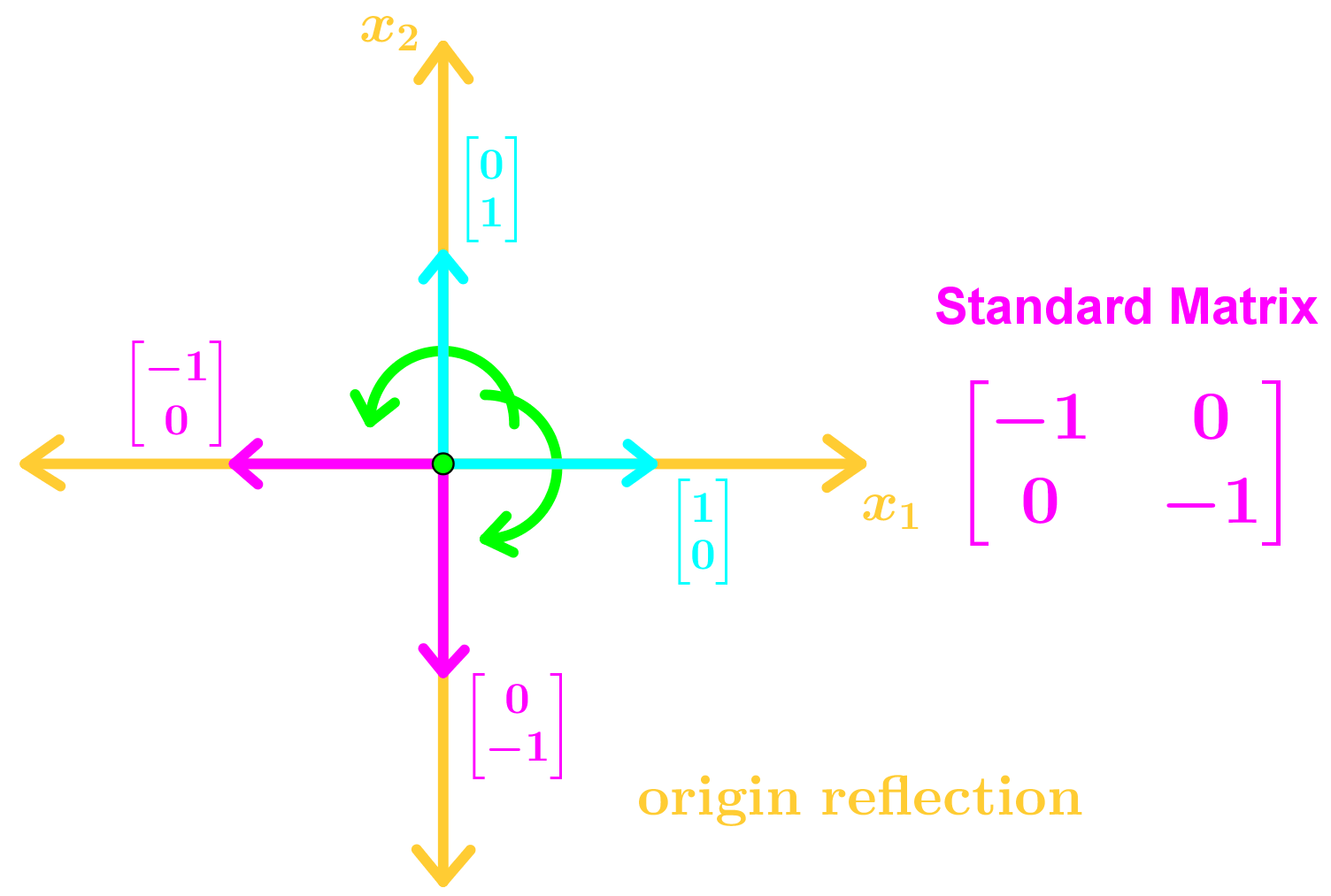
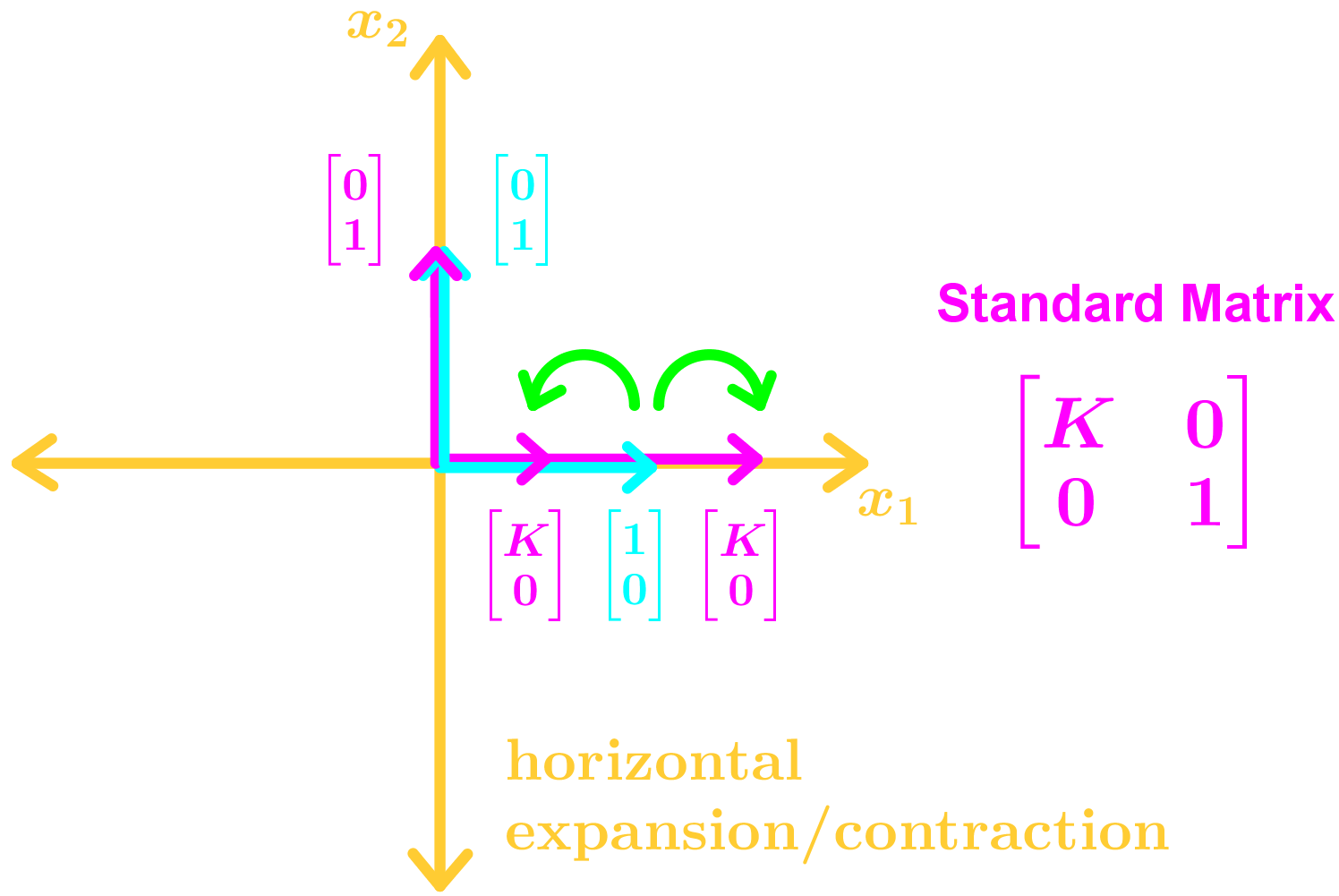
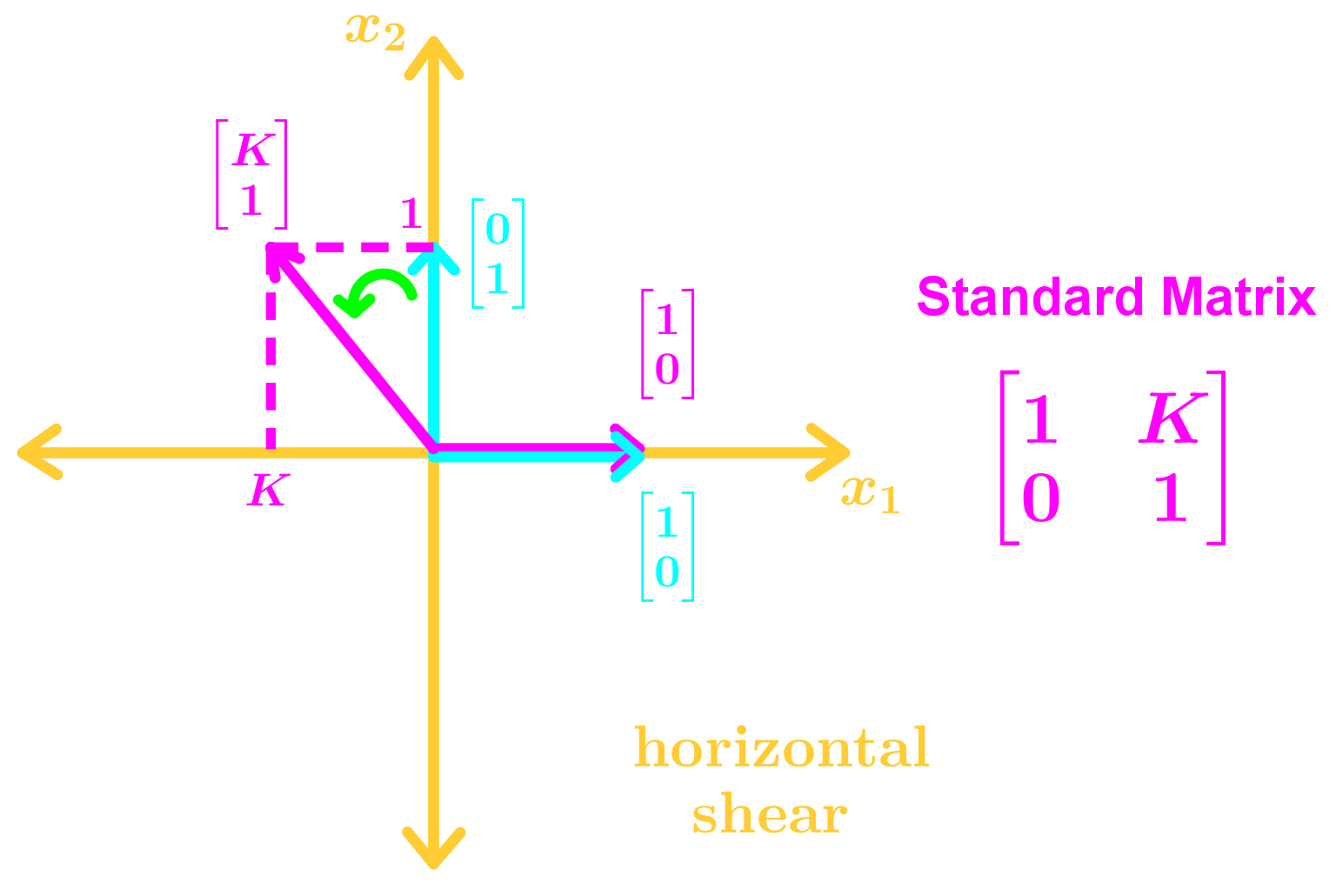
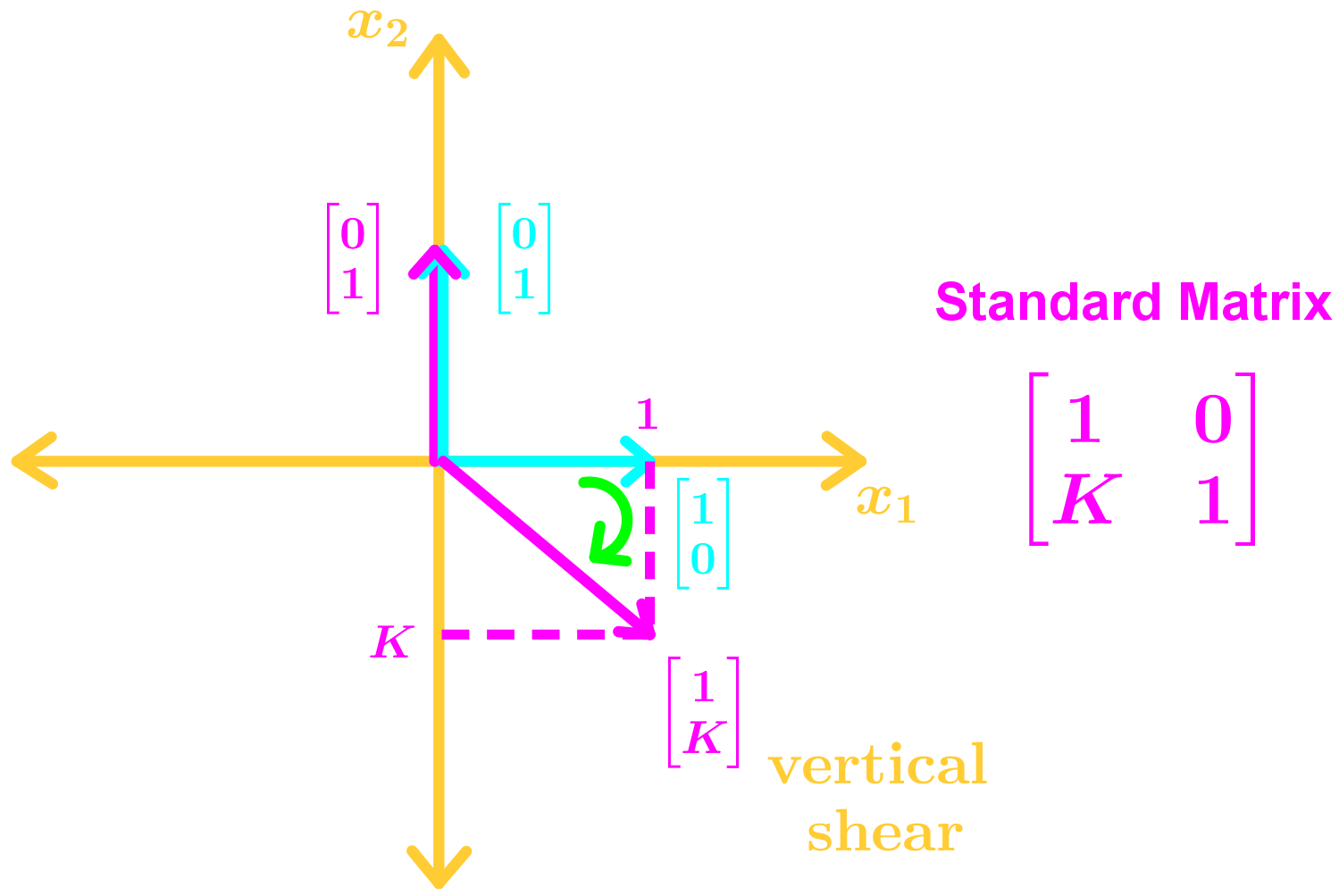
- Types of Geometric Linear Transformations in R2
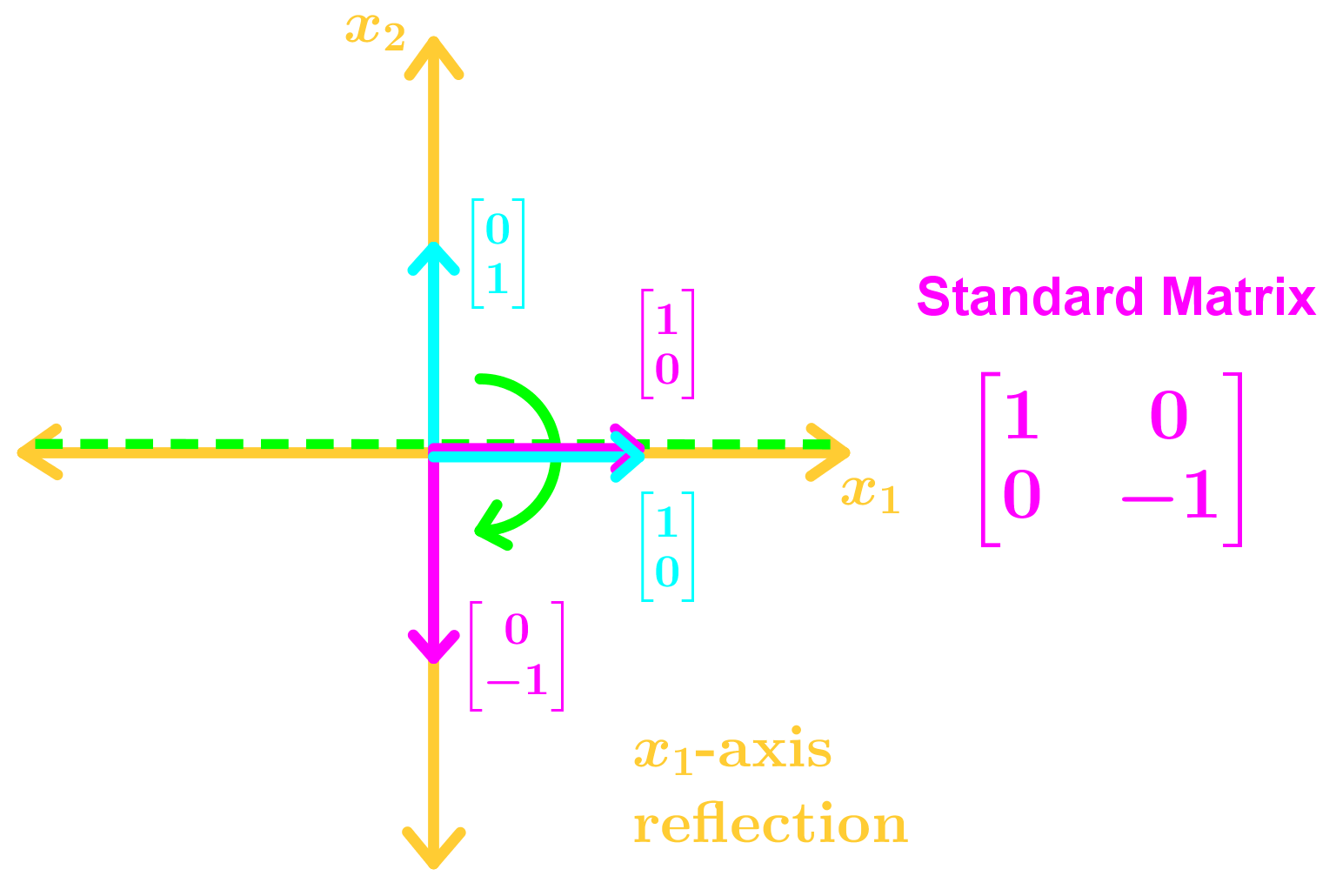
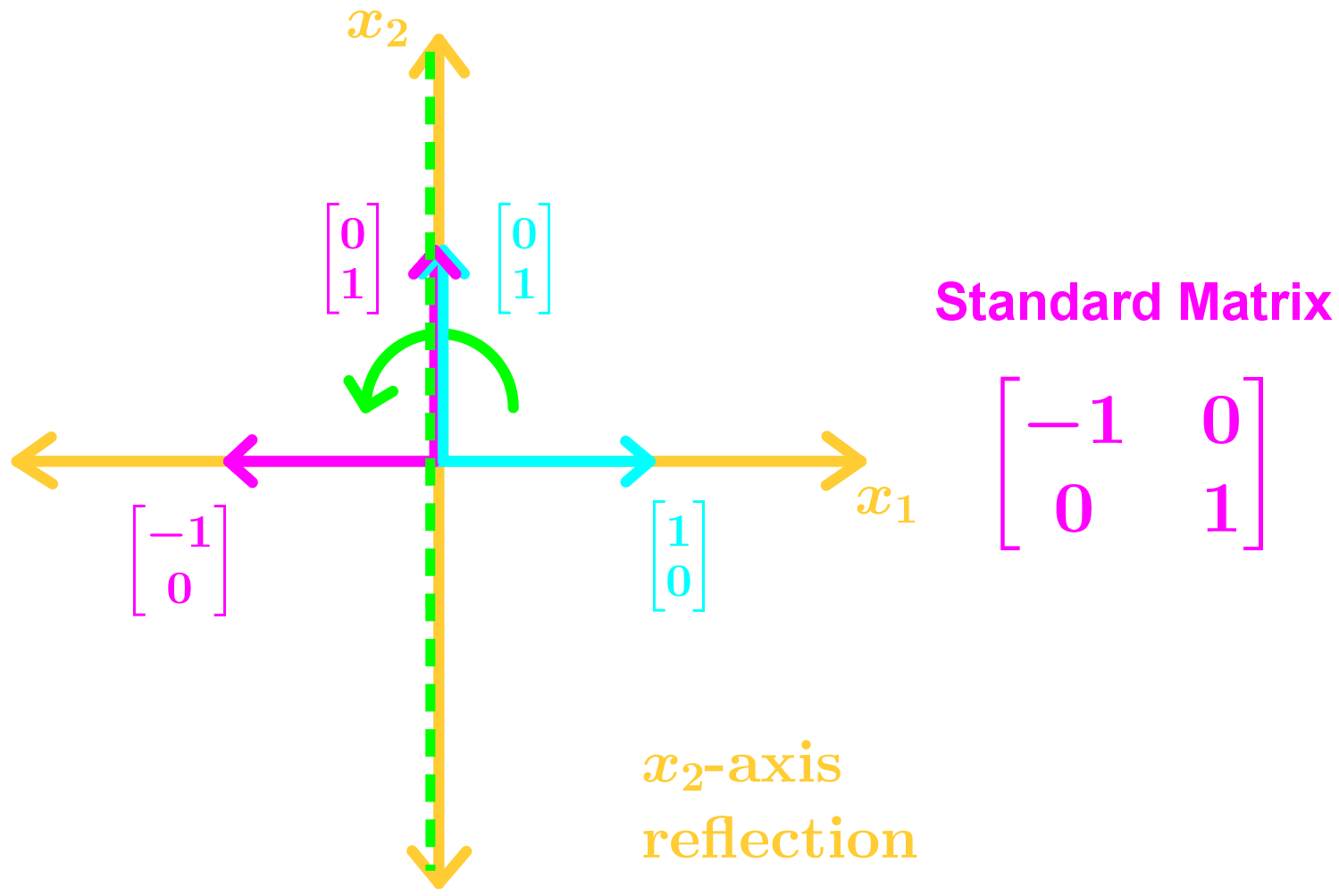
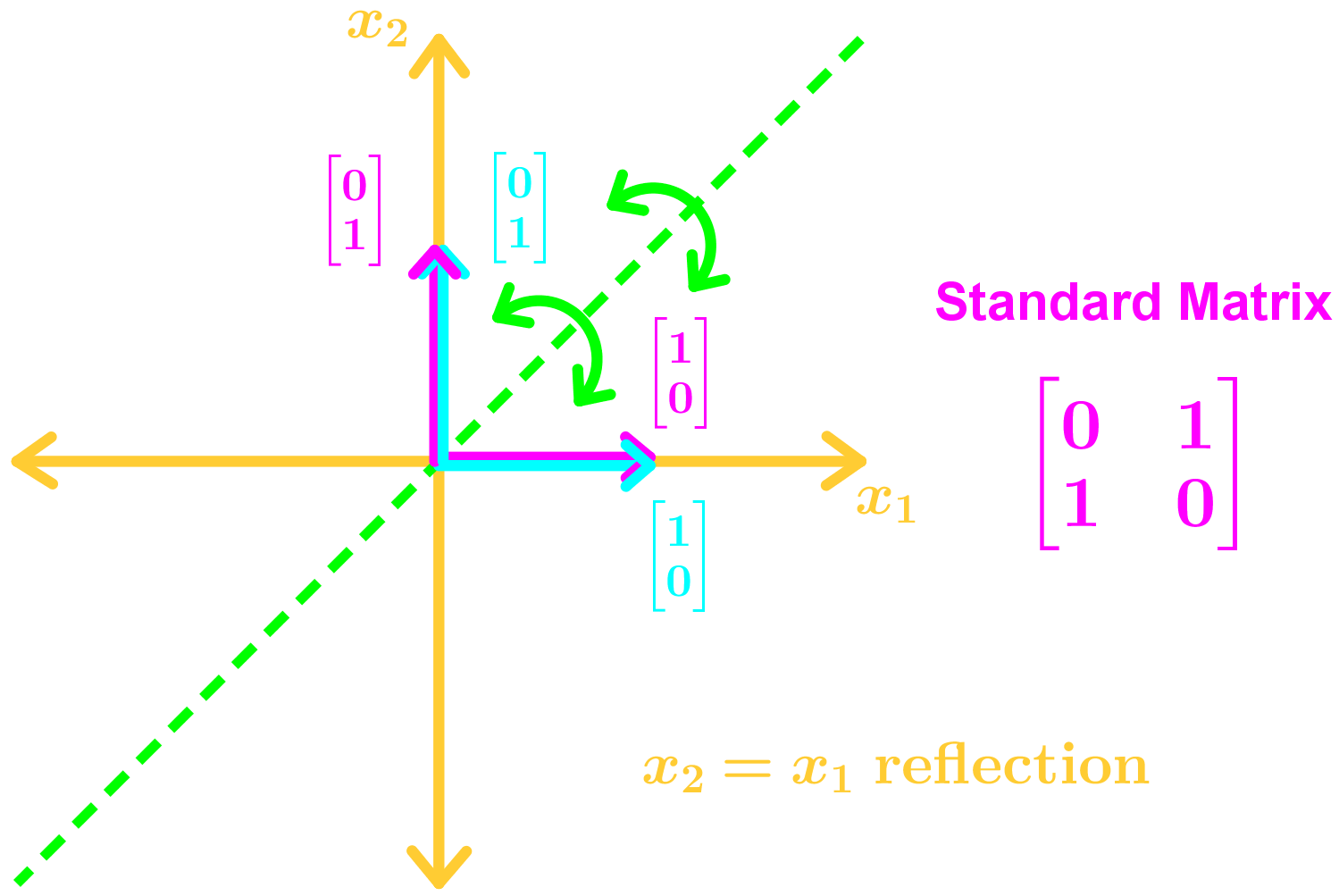
• Reflections on a Line
• Horizontal Expansion/Contraction
• Vertical Expansion/Contraction
• Horizontal & Vertical Shears
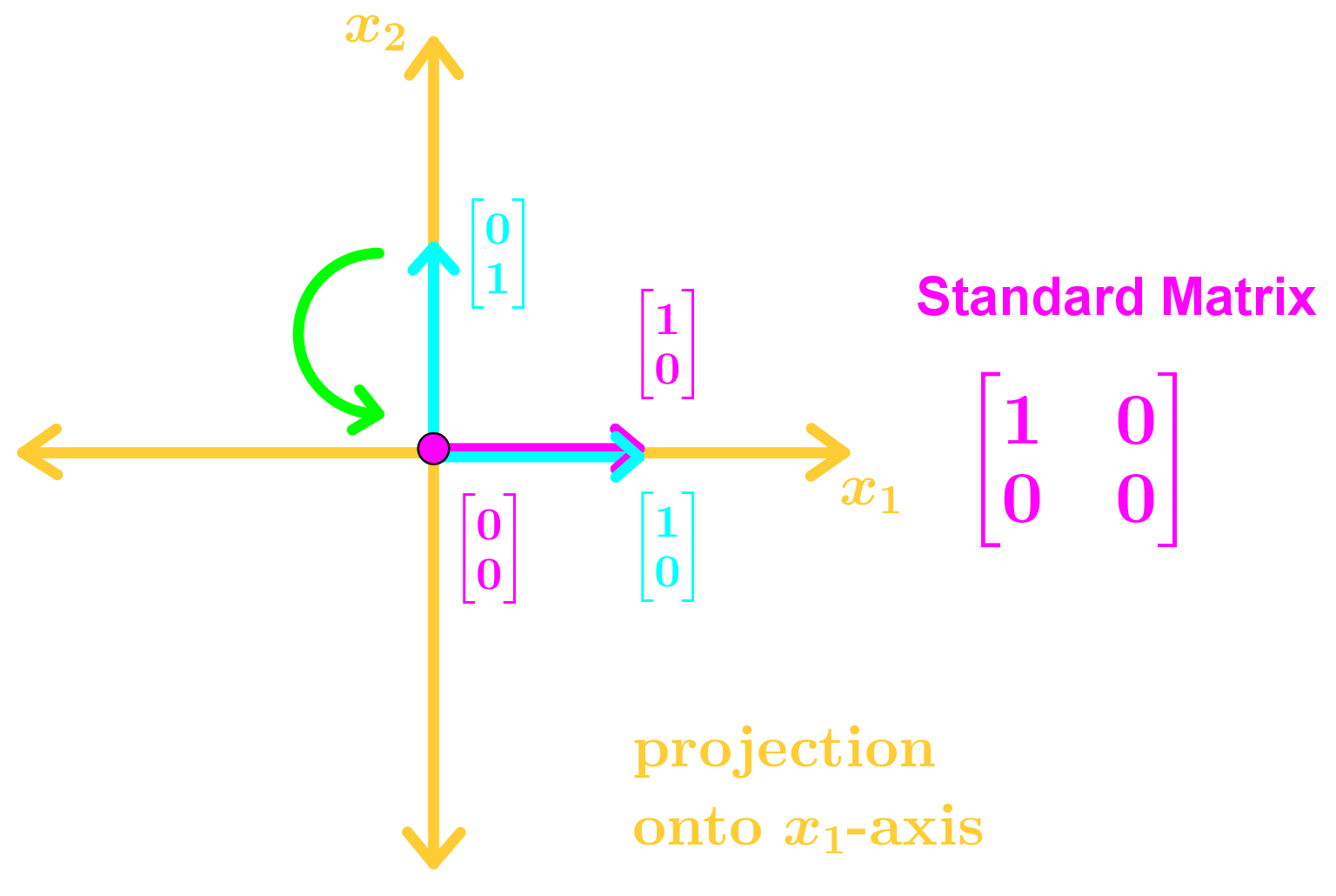
• Projections
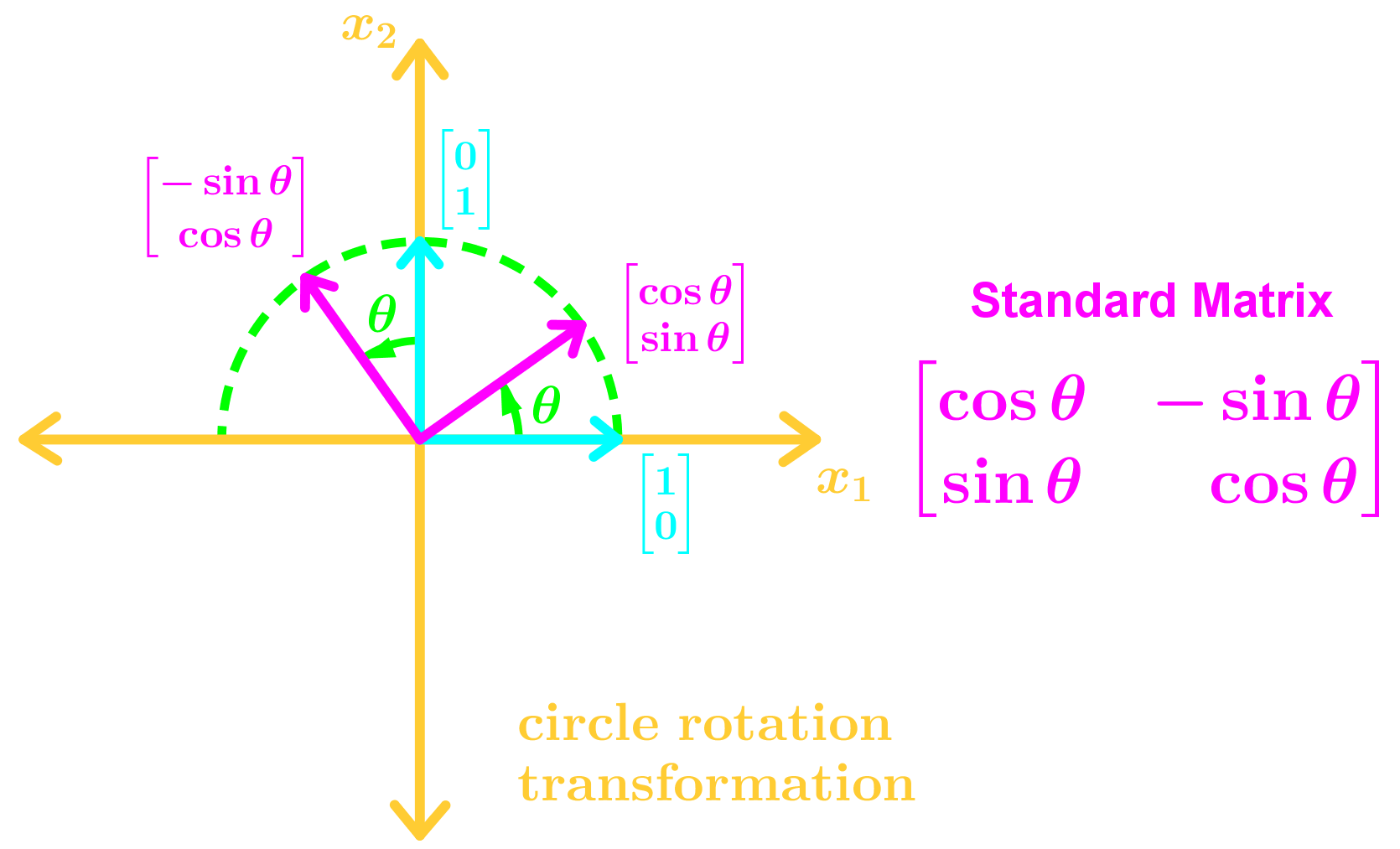
• Rotation Transformations
Examples
Lessons
- Finding the Standard Matrix with Transformed Basis
Assume that T is a linear transformation. Find the standard matrix of T if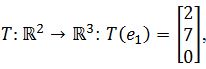
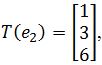 where
where ![standard matrix of T, e1= [1 0]](https://dcvp84mxptlac.cloudfront.net/diagrams2/LA-2-4-X-1_3.jpg) and
and ![standard matrix of T, e2= [0 1]](https://dcvp84mxptlac.cloudfront.net/diagrams2/LA-2-4-X-1_4.jpg) .
. - Assume that T is a linear transformation. Find the standard matrix of T if
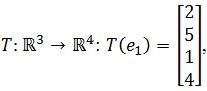
 where
where ![standard matrix of T, e1= [1 0 0], e2= [0 1 0]](https://dcvp84mxptlac.cloudfront.net/diagrams2/LA-2-4-X-2_3.jpg) and
and ![standard matrix of T, e3= [0 0 1]](https://dcvp84mxptlac.cloudfront.net/diagrams2/LA-2-4-X-2_4.jpg) .
. - Finding the Standard Matrix Geometrically
Assume that T is a linear transformation. Find the standard matrix of T if T:R2→R2 is a vertical shear transformation that maps e1 to e1+2e2 and leaves e2 unchanged. - Assume that T is a linear transformation. Find the standard matrix of T if T:R2→R2 first performs a x2=x1 reflection, and then a x1 reflection.
- Finding the Matrix Algebraically
Show that T is a linear transformation by finding a matrix A that implements the mapping:
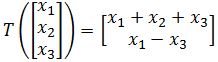
- Finding for x given the Transformation
Let T:R2→R2 be a linear transformation such that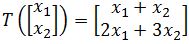 . Find a x such that
. Find a x such that 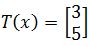
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
The matrix of a linear transformation
What is a linear transformation
From our lesson on the image and range of linear transformations we learnt that a linear transformation is a technique in which a vector gets "converted" into another by keeping a unique element from each of the original vector and assigning it into the resulting vector. This process basically maps one vector space into another. There may be different kinds of transformations in mathematics but the case of a linear transformation in linear algebra is that which preserves linear combinations from the original expression to the resulting one, in simple words, it preserves the way addition and scalar multiplication operate from the original vector to the transformed vector. A linear transformation example can also be called linear mapping since we are keeping the original elements from the original vector and just creating an image of it.
Recall the matrix equation Ax=b, normally, we say that the product of A and x gives b. Now we are going to say that A is a linear transformation matrix that transforms a vector x into a vector b (we now call b an image of a linear transformation of x).
In a sense Ax is a function where if we plug in a vector, then it spits out another vector. If we call this function T(x), then T(x)=Ax, where T is the transformation. Note that T(x) is an image of x since T(x)=b;
The matrix of a linear transformation
So, let us define once more a linear transformation in mathematical form:
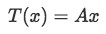
Where T(x) is read as "the transformation of x", x is the initial vector, and A is the transformation matrix. We will focus on this A this is what we call: the standard matrix of a linear transformation.
During this lesson, we will focus on methods to solve for the standard matrix A when you are given a linear transformation of a vector.
Let us start by describing the three main methods we use to solve such problems and then we will jump into examples of such exercises.
How to find the standard matrix of a linear transformation
There are three methods we can use to obtain the standard matrix of a linear transformation:
- Calculating the standard matrix using the transformed basis:
For a two dimensional basis, when using this method, we are provided with the unit vectors e1 and e2 and with the transformed basis vectors T(e1) and T(e2) to start with. If we are talking about a three-dimensional basis then we are provided with the unit vectors e1,e2 and e3 and the transformed vectors T(e1), T(e2) and T(e3). Then, the steps to follow to obtain the standard matrix are:
- Use the definition of a linear transformation: T(x)=Ax and define the vector x.
- Expand vector x into its components until is written in terms of the unit vectors and its variables x1,x2,...,xn.
- Use the expansion of vector x and perform the linear transformation T(x)=Ax.
- Expand the transformation T(x) until is in terms of the transformed vectors T(e1), T(e2) , ... , T(en) and the variables x1,x2,...,xn.
- Then rewrite this expression from the transformation as the matrix multiplication Ax.
- You have found the matrix A.
Notice that the standard matrix found is composed of the transformed vectors T(e1), T(e2) , ... , T(en). Technically, you could very well skip this whole process and just write down the matrix using the provided transformed vectors, BUT, you need to know how they were derived (plus your teacher may not accept this solution without an explanation). So make sure you understand the whole process.
Examples of this method are found in example exercises 1 and 2 in our next section.
- Finding the standard matrix geometrically:
To find a standard matrix geometrically means to find it using a cartesian coordinates graph, actually draw the vectors involved, see the transformations they go through and obtain from the result a new matrix: the standard matrix. The steps to follow to find a standard matrix geometrically for a two-dimensional basis are:
- Draw the standard basis e1 and e2 in the x1x2−plane.
- Obtain the transformed vectors T(e1) and T(e2).
- Draw the transformed vectors using the information provided in the problem.
- Combine the transformed vectors to produce the standard matrix.
Notice that are providing the steps for a two-dimensional basis only, since we can a two-dimensional coordinate plane only (actually, you can also draw a three-dimensional plane, but it gets a bit complicated. Further than three dimensions we cannot draw them, and so, we use other techniques to solve for transformations with such bases).
For a step by step explanation on how to use this method, look at example 3 in our last section for this lesson.
- Computing the standard matrix algebraically:
The algebraic computation in order to find the standard matrix of a linear transformation can be done easily when the problem provides the complete expression for the linear transformation T(x)=Ax. In other words, once you have the initial vector x and the final vector Ax, you can use these expressions to solve for the matrix A.
The steps to follow in order to solve a problem this way are:
- Expand the given expression of the linear transformation resulting vector into an addition of vectors for each of the different variables inside.
- Factor out the variables x1,x2,...,xn from each of the column vectors.
- Form a matrix multiplication by rearranging the resulting column vectors from our last step into a matrix, and then multiplying it for the vector x which is the column vector containing all of the variables x1,x2,...,xn.
- The matrix that was formed in our last step is the standard matrix of the linear transformation.
An example of this process can be seen in the exercise example 4 in our next section.
Notice that this is probably the simplest methods to use, and if you are given all of the necessary information and have to be time-effective while solving an exercise on this, we recommend you to use this method.
Linear transformation matrix examples
During the first two examples we will be finding the Standard Matrix using a transformed basis, then we will see two examples on how to find the standard matrix geometrically. We finish off with an example where we will compute the standard matrix algebraically.
Example 1
Assume that T is a linear transformation. Find the matrix representation of linear transformation T (the standard matrix) if:
Where the unit vectors are defined as follows:
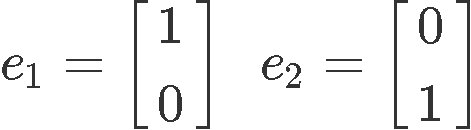
To answer this question we could literally just take the vectors resulting from the linear transformation of the unit vectors e1 and e2, put them together into a matrix and that would be our standard matrix, but how does that work? Let us derive it then!
We know that a linear transformation of a matrix A has the form: T(x)=Ax, therefore, we need a vector x to perform the transformation. For this case our vector x must have two entries, and so, vector x is (notice this is just any vector x in two dimensions):
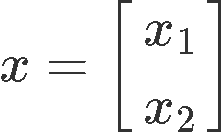
We can expand this vector x into an addition of vectors and factor out their components in order to have the unit vectors which form part of it visible, just look at how we have expanded it below:

And now, it can clearly be seen how the vector x is composed by the variables x1 and x2, and the set of unit vectors e1 and e2. Thus we can rewrite this last equation as:
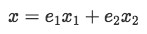
So we take the linear transformation of vector x which goes as:
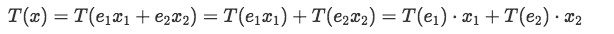
Notice how the linear transformation affects the unit vectors only, this is because those are the ones establishing the direction of the vector and a linear transformation usually changes that (remember it can rescale a vector too, but the most common cases it preserves its magnitude, but rotates it with respect of a certain axes). So, since we know what T(e1) and T(e2) are we can rewrite the transformation as:
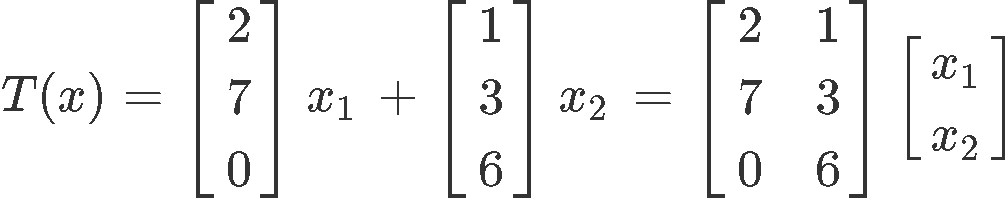
Where the standard matrix of a linear transformation as the one represented in equation 2 is:

Example 2
Assume that T is a linear transformation. Find the standard matrix of linear transformation T if: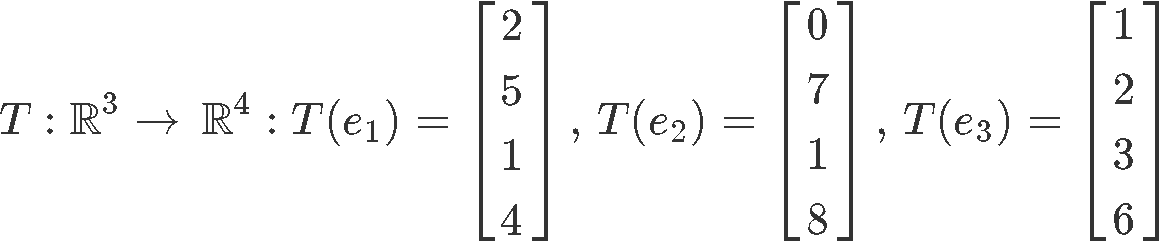
where the unit vectors are defined as:
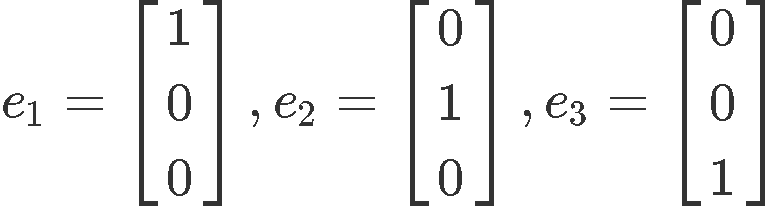
A linear transformation of a matrix A has the form: T(x)=Ax, thus, we start by expanding the vector x into its components once more:

We can observe how vector x is composed by the variables x1,x2 and x3, and the set of unit vectors e1,e2 and e3. Thus we can rewrite this last equation as:
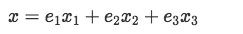
So we take the linear transformation of vector x which goes as:
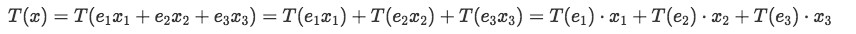
Since we know what T(e1), T(e2) and T(e3) are we can rewrite the transformation as:
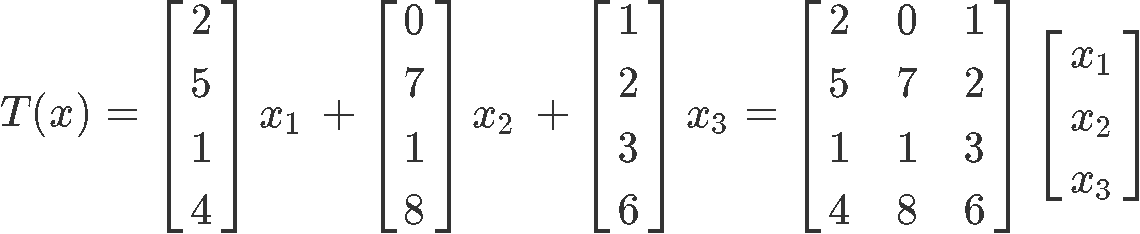
And so, the standard matrix is:

Example 3
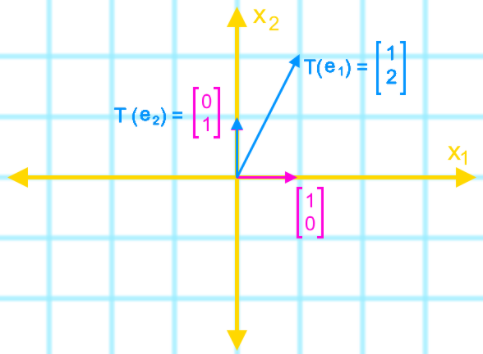
Assume that T is a linear transformation. Find the matrix of the linear transformation T if T: R2→R2 is a vertical shear transformation that maps e1 to e1+2e2 and leaves e2 unchanged.Let us first define the standard basis for this problem, given that we are talking of a 2-dimensional vector space R2, then this means our standard basis unit vectors are:
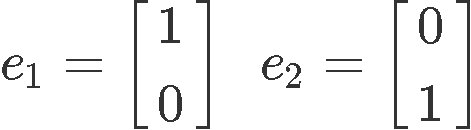
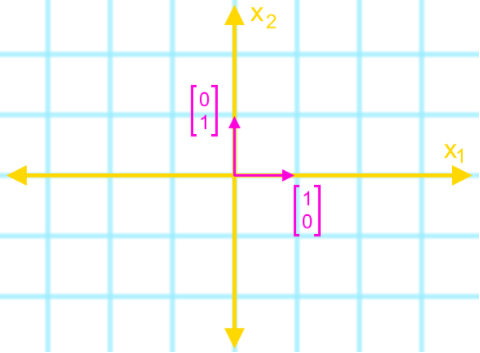
For this example we will use the steps summarized on the method to find a standard matrix geometrically:
The transformation provided is defined as: e1 to e1+2e2 and e2 unchanged. Using the standard basis unit vectors we can define the transformations as:
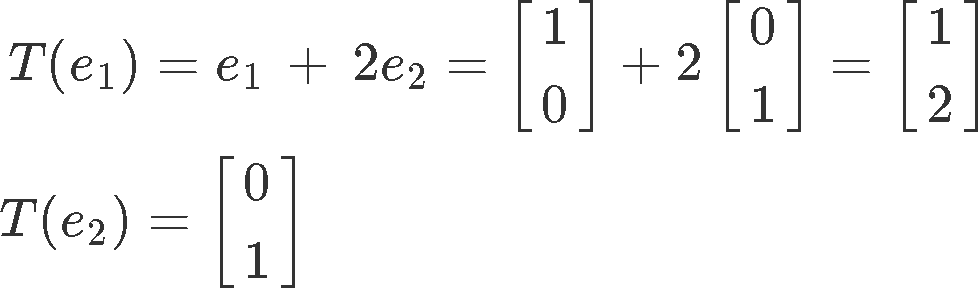
Notice that T(e2)=e2 because the transformation is defined to leave the basis unchanged.

Example 4
Show that T is a linear transformation by finding a matrix A that implements the mapping:
This is the easiest method to use when given the linear transformation definition, the only thing to do is to separate the vector given into its variables' individual vectors:

We can rewrite the transformation above as follows, by factoring out of the column vectors the variables x1, x2 and x3:
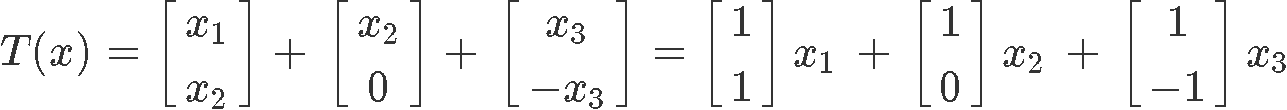
And so, now we can see how the transformation fits with the formula for a linear transformation T(x)=Ax by rewriting it once more as the appropriate matrix multiplication of A and the column vector x:

Therefore, the linear transformation matrix, or standard matrix A is:
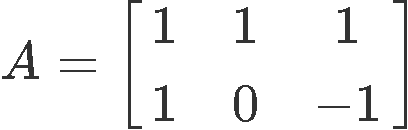
Now that you have learnt how to compute linear transformations and their corresponding standard matrices, we would like to finalize our lesson be recommending you to take a look into this lesson on linear transformations from Rn to Rm, where you can see some more examples and graphs with the transformations explained. We also recommend this lesson named Google search since it goes even deeper on the subject matter by introducing some calculus level computations and linear transformation applications.
So, this is it for our lesson of today, we hope you enjoyed it. Make sure to work through the exercises and see you on the next one!
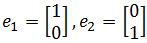
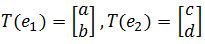 are the transformed vectors, then the standard matrix is
are the transformed vectors, then the standard matrix is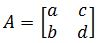
Why does that work? Watch the intro video
The standard basis, e1, e2, and e3 are unit vectors in R3 such that:
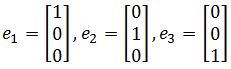
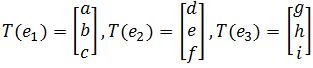 are the transformed vectors, then the standard matrix is
are the transformed vectors, then the standard matrix is 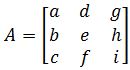
To find the standard basis in R2 geometrically in a graph we:
1. Draw the standard basis e1 and e2 in the x1x2 plane
2. Draw the transformed vectors using the information given
3. Identify the transformed vectors T(e1), and T(e2).
4. Combine them to get the standard matrix
Here are the many types of transformations you may see in this section:


remaining today
remaining today



