Eigenvalue and eigenvectors
All in One PlaceEverything you need for JC, LC, and college level maths and science classes. | Learn with EaseWe’ve mastered the national curriculum so that you can revise with confidence. | Instant Help24/7 access to the best tips, walkthroughs, and practice exercises available. |
Make math click 🤔 and get better grades! 💯Join for Free
0/3
Intros
Lessons
- Eigenvalues and Eigenvectors Overview:
- Definition of Eigenvalues and Eigenvectors
• What are eigenvectors?
• What are eigenvalues? - Verifying Eigenvalues/Eigenvectors of a Matrix
• Eigenvectors: Show that Ax=λx
• Eigenvalues: Get a non-trivial solution for (A−λI)x=0
• Finding a eigenvector given an eigenvalue - Eigenspace
• What is an eigenspace?
• Finding a basis for the eigenspace
0/6
Examples
Lessons
- Verifying Eigenvectors
Let . Is
. Is 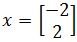 an eigenvector of A? If so, find the eigenvalue. What about
an eigenvector of A? If so, find the eigenvalue. What about 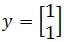 ?
? - Let
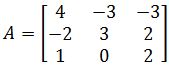 . Is
. Is 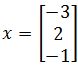 an eigenvector of A? If so, find the eigenvalue.
an eigenvector of A? If so, find the eigenvalue. - Verifying Eigenvalues and finding a corresponding eigenvector
Let . Is λ=1 an eigenvalue of A? If so, find a corresponding eigenvector.
. Is λ=1 an eigenvalue of A? If so, find a corresponding eigenvector. - Finding a Basis for the Eigenspace
Find a basis for the corresponding eigenspace if:
- Proof Related to Eigenvalues and Eigenvectors
Prove that if A2 is the zero matrix, then the only eigenvalue of A is 0. - Let λ be an eigenvalue of an invertible matrix A. Then λ−1 is an eigenvalue of A−1.
Free to Join!
StudyPug is a learning help platform covering maths and science from primary all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Eigenvalues and Eigenvectors
During our lesson about the image and range of linear transformations, we learnt that a linear transformation T(x)=Ax re-scales a vector without changing its direction. Now it is time to talk about that vector x, an eigenvector, where does it come from and how is it related to the given matrix A.
What are eigenvalues and eigenvectors
In order to understand what an eigenvalue is we have to define an eigenvector first.
For any given square matrix A, an eigenvector is a non-zero vector x such that Ax=λx, for some scalar . In other words, an eigenvector is a non-zero characteristic vector (column vector) which changes by a constant factor (which we name "lambda"= λ) when a square matrix is applied to it through matrix multiplication.
Then the eigenvalue is this constant factor, the eigenvalue is λ .
Given this, now we know that all nxn matrices happen to have an eigenvector that corresponds to an eigenvalue. And so, for this condition of correspondence between an eigenvector and eigenvalue is defined as:
we say that the eigenvector x corresponds to the eigenvalue λ .
- Verifying Eigenvectors
First, the column vector x given MUST have the same amount of entries as the matrix A has rows, if not, the multiplication Ax is not possible. Second, the vector x cannot be a zero vector. This second requirement will come back when we are verifying eigenvalues in the next part of this section.
The steps to verify if a given column vector x happens to be an eigenvector of the matrix A are:
- Multiply the matrix A times the vector x.
- The resulting vector should be equal to the multiplication of λ times the vector x.
- A constant value should be possible to be factored out of the resulting vector in order to leave the multiplication of this constant value times the vector x. This value will be λ.
- In other words, you should be able to factor out the vector x from the vector resulting from Ax.
- Once you have factored out the vector x, there will be a constant factor multiplying it.
- This constant factor will be the eigenvalue λ .
- If there is no constant value that can be factored out of the resulting vector from Ax, which will produce a multiplication with the vector x, then it means that x is NOT an eigenvector.
We will demonstrate this process with a few exercises on a later section of this article, for now, let us look at the verification process for eigenvectors.
- Verifying Eigenvalues
And find a non-trivial solution. Here the I represents the identity matrix, therefore, the multiplication Iλ always produces a diagonal square matrix where the elements of its diagonal are all λ and the rest of the values in the matrix are all zeros.
In order for the λ value of to be an eigenvalue the resulting vector must contain a non-trivial solution because a trivial solution means that this resulting vector is a zero vector. It so happens that this resulting vector is the column vector x (from equation 1) which is the corresponding eigenvector of the λ value provided. Therefore, if the result is a trivial solution this would mean that x is a zero vector, which we know (from the last part of this section) that it cannot be a zero vector.
And so, the value of λ is an eigenvalue of the matrix A ONLY when the resulting vector x has a non-trivial solution.
The steps to verify if a given λ happens to be an eigenvalue of the matrix A are:
- Perform the subtraction between the matrices A and Iλ (dont forget to substitute λ with its constant value) to obtain a new matrix.
- The multiplication of the new matrix with vector x can be rewritten into an augmented matrix.
- Row reduce the augmented matrix into an echelon form in order to find the components of the vector x.
- Once you find the components of x, if the result is a non-trivial solution, then it means λ is an eigenvalue of A and its corresponding eigenvector is x.
- If a trivial solution is found, then it means λ is not an eigenvalue of A.
Once more, the verification process process will be shown in the exercises later during our lesson.
Calculating eigenvalues and eigenvectors
The calculation of eigenvalues is done through an algebraic expression called the characteristic polynomial equation:
We will dedicate our next lesson to learn all about the characteristic equation, still, we will briefly explain the way how to do the calculations to obtain eigenvectors and eigenvalues using it, but will not go into detail of its origin or its usage in other cases.
Notice in equation 3 that inside of the determinant of the characteristic equation, there is a subtraction of the given n×n square matrix A and the scalar multiplication of the identity matrix and the eigenvalue λ . That subtraction will produce another matrix, therefore, once we compute the determinant of that matrix the result will be an algebraic second degree expression where λ will appear as a variable, and for which we have to solve its roots.
And so, the computation of eigenvalues happens to be a simple calculation that can be done using the quadratic formula.
But this lesson is called eigenvalues and eigenvectors for a reason: Since an eigenvalue is a root of a quadratic equation, we can automatically understand there is usually more than one eigenvalue associated to a given square matrix. With that in mind, you should know that for each eigenvalue there is a corresponding eigenvector. And so, the main purpose of obtaining the eigenvalues of a matrix is to then produce its set of corresponding characteristic column vectors, its eigenvectors. For that we go back to equation 2.
Once you have calculated the eigenvalues associated to an square matrix, the process to obtain its corresponding eigenvectors is just what we have called the steps for verifying eigenvalues in our last section (remember you will be computing the components of vector x during that process? That is basically finding the vector x which is the eigenvector associated to the given eigenvalue). In summary, the complete steps to find all eigenvalues and eigenvectors of the given matrix are:
- Find the eigenvalues using the characteristic equation described in equation 3
- Calculate the roots for the resulting quadratic equation from the determinant using the quadratic formula.
- Use the eigenvalues found in order to compute the eigenvectors through equation 2.
- Transform the matrix equation (A−Iλ)x=0 into an augmented matrix.
- Use the row-reduction method in order to obtain the final column vector x.
- x is the eigenvector associated to λ.
- Repeat step 2 for each eigenvalue we found in step 1, and so, produce at least the same amount of eigenvectors as eigenvalues found.
That pretty much sums up the complete process to calculate eigenvalues and eigenvectors, as you can see, there is really not much more to say about how to find the eigenvalues and eigenvectors of the matrix A. Still, we will retake this topic in our next lesson, since the characteristic equation in linear algebra is mainly used to find eigenvalues and eigenvectors, thus, the process will be re-described adding any appropriate detail that may not be useful for the moment.
Before we continue onto our next section where we will be working through eigenvalues and eigenvectors examples, let us talk a little bit about what is an eigenspace:
The eigenspace is the set of all the solutions for the equation (A−Iλ)x=0, thus, its basis is represented as the general solution containing the collection of all of the vectors x that satisfy that equation (equation 2). Therefore, an eigenspace provides a look at all of the possible eigenvalues and their corresponding eigenvectors by conforming a set of vectors where the elements inside of it are the zero vector and all of the possible eigenvectors of the given matrix. In simple words, the eigenspace of a matrix is the null space of the matrix resulting from A−Iλ.
The general steps to follow in order to find the basis for the eigenspace corresponding to a given matrix and an eigenvalue are:
- Set up the equation (A−Iλ)x=0.
- Calculate the resulting matrix from A−Iλ.
- Use such matrix to form an augmented matrix in order to solve for x
- When finding the components of vector x, use all of the free variables to conform the set of possible vectors for the general solution of x.
- Repeat this for every eigenvalue available for the given matrix.
This process will be shown in example 4 in our next section.
Eigenvalues and eigenvectors examples
Example 1
If the square matrix A and the vector x are defined as follows: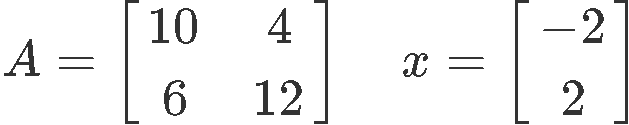
- Is x an eigenvector of A? If so, find the eigenvalue.
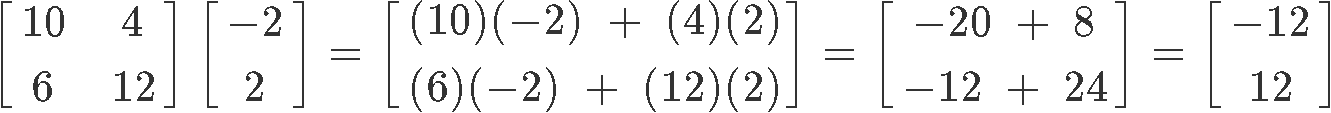
The column vector resulting from equation 5 is equal to λx, and so, we need to find a scalar that can be factored out of the vector in order for this condition (equation 1) to be satisfied:

And so,λ=6 is the eigenvalue corresponding to vector x, proving that x is an eigenvector.
- If we are to have another column vector named y which is defined as:
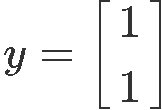
Is y an eigenvector of A?
We work with the correspondence condition once more as follows:
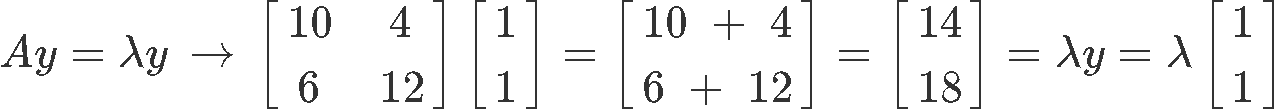
Notice there is no possible value of λ that could satisfy the condition, and so, vector y is NOT and eigenvector for matrix A.
Example 2
Having the following 3x3 matrix A and column vector x:
Is x an eigenvector of A? If so, find the corresponding eigenvalue.
Once more, we start by computing the left hand side of the condition Ax=λx:
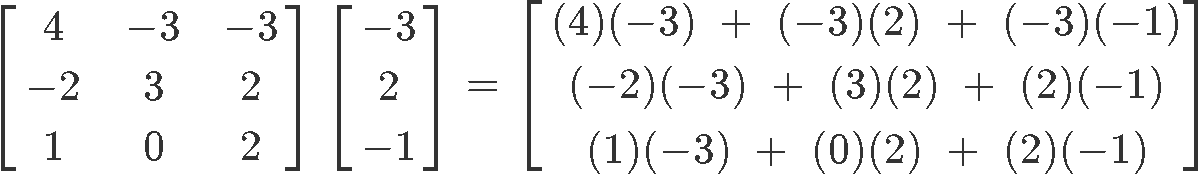
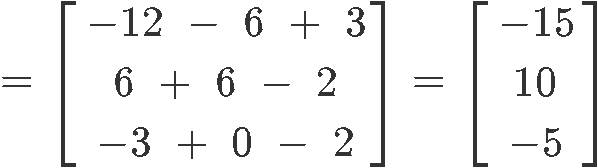
Using the resulting column vector, lets see if we can factor out a scalar to satisfy the condition of correspondence, and find an eigenvalue:
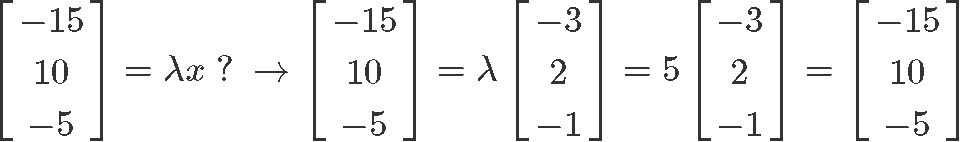
Therefore, x is an eigenvector, and its corresponding eigenvalue isλ=5.
And this is how we find the eigenvalues and eigenvectors for the coefficient matrix A. The next example shows a similar problem, but instead of starting with a known eigenvector, we start with a potential eigenvalue:
Example 3
Having the following 3x3 matrixA: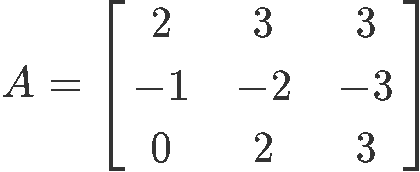
Is λ=1an eigenvalue of A? If so, find its corresponding eigenvector of A.
In order to verify an eigenvalue, we use equation 2: (A−Iλ)x=0. Therefore, let us start by computing the subtraction of matrices A−Iλ:
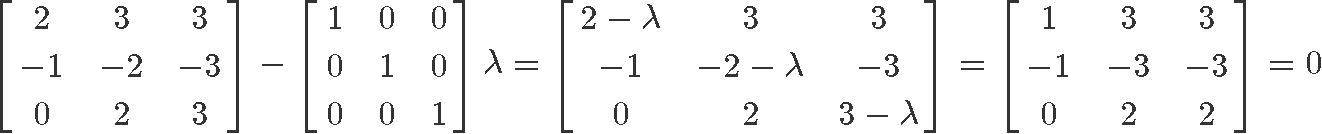
Notice how we have equated the subtraction A−Iλ to zero, this is because in order for x to be an eigenvector, x must be a non-zero vector. Therefore, to satisfy (A−Iλ)x=0 it means that the matrix resulting from the subtraction shown in equation 12 MUST be equal to zero: A−Iλ=0
And so, we can convert the relationship (A−Iλ)x=0 into an augmented matrix to solve for x:
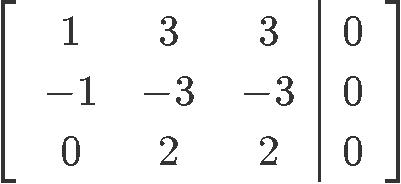
Row reducing the augmented matrix in order to find the vector x:
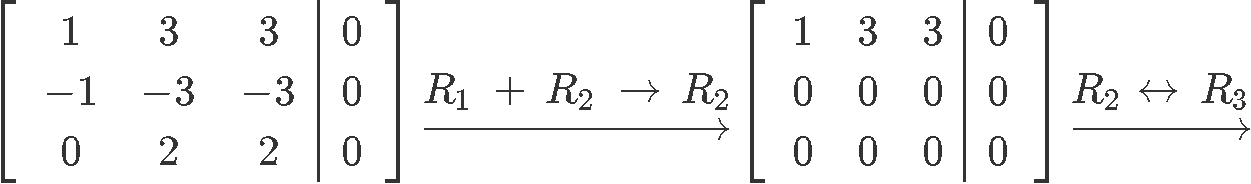

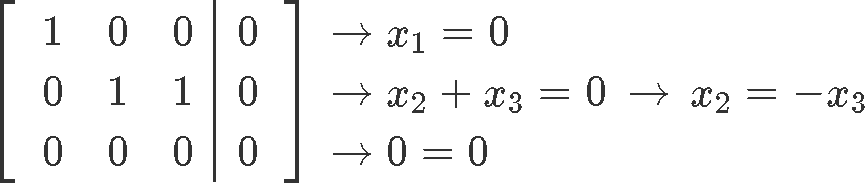
From equation 14 notice that x3 is a free variable since it doesnt have a corresponding pivot, and so, we have obtained the components for vector x:
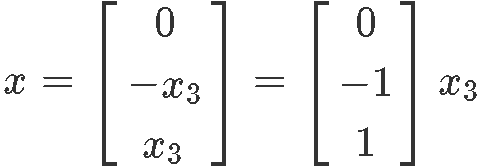
Since x3 is a free variable, we can set it up to any value we want, in this case, for practicality, we set x3=1 and our resulting vector x is:
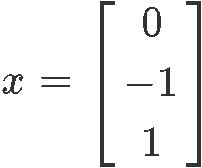
As we can observe from example 2 and 3, that finding eigenvalues and eigenvectors go hand in hand, and so, most problems expect you to find either the eigenvalues and eigenvector associated to them, or vice versa.
Example 4
Find a basis for the corresponding eigenspace if:
We calculate the matrix subtraction A−Iλ
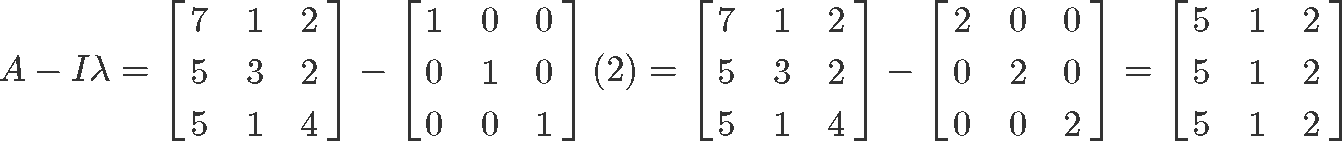
Using equation 2: (A−Iλ)x=0, we set up an augmented matrix in order to solve for the vector x:
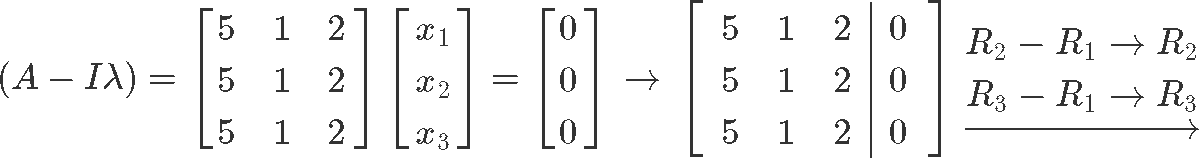
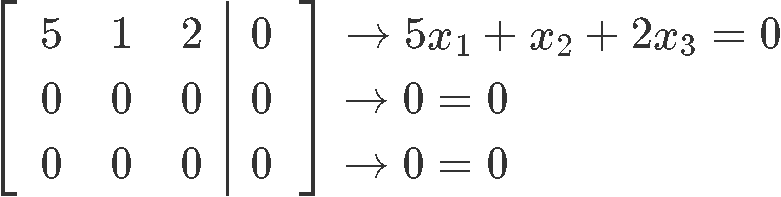
From equation 20 we can observe that x2 and x3 are both free variables. So we solve for x1:
And we can finally write down vector x by setting the free variables both equal to 1.
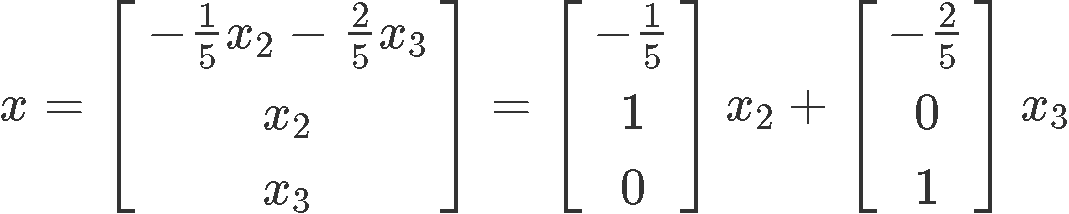
And the basis for the eigenspace is:

Now that we have seen the definition of eigenvalues and eigenvectors, along with what an eigenspace is, let us comment a little bit about the uses of eigenvalues and eigenvectors: When studying rotational motion of rigid objects, the concept of eigenvectors determines the principal axes through which a body can be rotated (change its state) following the principles of Newton laws of motion, thus, the concepts of eigenvalues and eigenvectors contribute to the toolbox when working on problems for the mechanics of bodies.
And so, after learning the core process on how to find eigenvalues and eigenvectors of a matrix, we finalize this section by providing you with a few recommendations on links we think may be useful for your independent studies: First we suggest you to visit this review on eigenvalues and eigenvectors, since it contains a set of extensively explained problems. This other linear algebra article on eigenvalues and eigenvectors shows the process using symmetric matrices.
This is it for this lesson, see you on the next one!
An eigenvector of an n×n matrix A is a non-zero vector x such that Ax=λx, for some scalar λ. The scalar λ is called the eigenvalue.
We say the eigenvector x corresponds to the eigenvalue λ.
Given an eigenvalue λ of matrix A, we can find a corresponding eigenvector x by solving
(A−λI)x=0
And finding a non-trivial solution x.
The eigenspace is the null space of the matrix A−λI. In other words, the eigenspace is a set of all solutions for the equation
(A−λI)x=0
Of course, we can find the basis for the eigenspace by finding the basis of the null space of A−λI.
We say the eigenvector x corresponds to the eigenvalue λ.
Given an eigenvalue λ of matrix A, we can find a corresponding eigenvector x by solving
The eigenspace is the null space of the matrix A−λI. In other words, the eigenspace is a set of all solutions for the equation
Of course, we can find the basis for the eigenspace by finding the basis of the null space of A−λI.
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today



