Introduction to probability
All in One PlaceEverything you need for JC, LC, and college level maths and science classes. | Learn with EaseWe’ve mastered the national curriculum so that you can revise with confidence. | Instant Help24/7 access to the best tips, walkthroughs, and practice exercises available. |
Make math click 🤔 and get better grades! 💯Join for Free
0/8
Examples
Lessons
- Below is a probability model showing the weathers in fall in City A.
Weather
Probability
Rain
0.35
Snow
0.08
Sunny
0.16
Cloudy
0.41
- Each student in a class of 30 writes his or her name on a slip of paper. These slips of paper are folded and put in a jar. Half of these slips are blue and half are yellow.
- What is the probability that a blue slip will be picked? Write your answer as a fraction, a decimal, a ratio, and a percent.
- Rob, Jennie and Alice are in this class. What is the probability that one of these students' names will be picked? Write your answer as a fraction, a decimal, a ratio, and a percent.
- Jen and her friend spin the wheel to decide what fun activity they will do this afternoon.
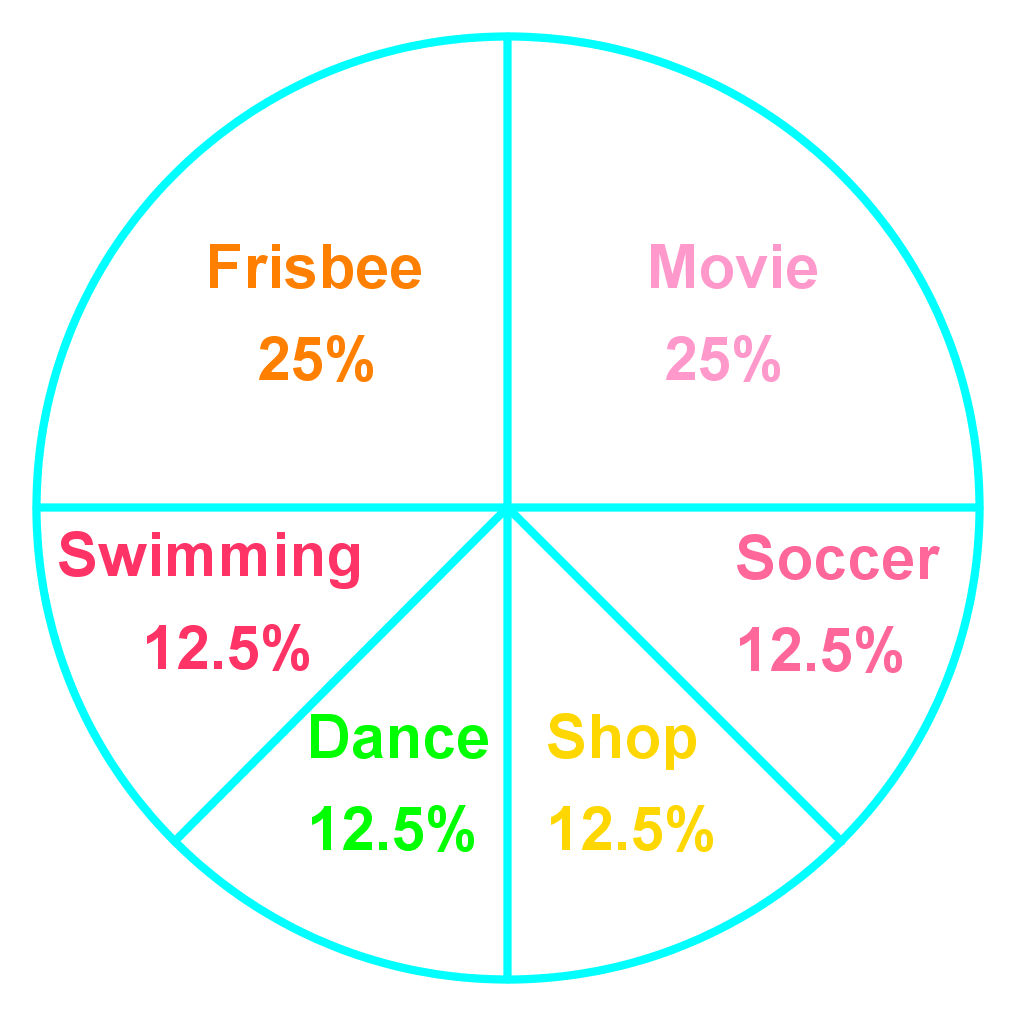
- What is the probability that the spin will land on movie or swimming? Write your answer as a percent and decimal.
- What is the probability that the spin will not land on dancing or shopping? Write your answer as a percent and fraction.
- If they spin the wheel twice, what is the probability that the spin will land on soccer and frisbee? Write your answer as a percent and fraction.
0%






