Scale diagrams
All in One PlaceEverything you need for JC, LC, and college level maths and science classes. | Learn with EaseWe’ve mastered the national curriculum so that you can revise with confidence. | Instant Help24/7 access to the best tips, walkthroughs, and practice exercises available. |
Make math click 🤔 and get better grades! 💯Join for Free
0/1
Intros
0/4
Examples
Lessons
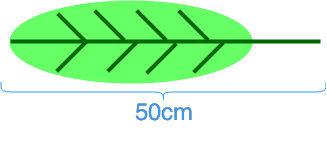
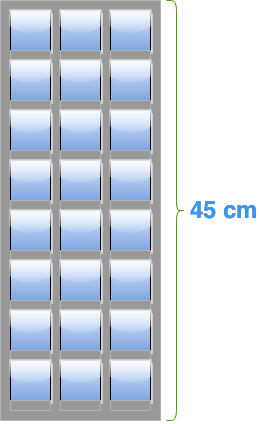
- What is the actual length of each object?
- Tony is 6 cm tall in a photo. Yet, his actual height is 1.86 m. What is the scale factor?
- A spaceship is 56 m in height. You have built a model of the spaceship with a scale factor of 1:60 for your cousin overseas. However, the longest shipping box you can find is only 0.8 m. Will the spaceship model fit into the shipping box?