Characteristic equation with real distinct roots
All in One PlaceEverything you need for JC, LC, and college level maths and science classes. | Learn with EaseWe’ve mastered the national curriculum so that you can revise with confidence. | Instant Help24/7 access to the best tips, walkthroughs, and practice exercises available. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
- Using the Characteristic Equation with Real Distinct Roots
Find the particular solution to the following differential equation:
y′′−9y=0
With initial values y(0)=2,y′(0)=1 - Find the particular solution to the following differential equation:
6y′′+8y′−8y=0
With initial values y(2)=1,y′(2)=4 - Find the particular solution to the following differential equation:
y′′−5y′+3y=0
With initial values y(0)=0,y′(0)=1
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Characteristic equation with real distinct roots
The characteristic equation
The characteristic equation of a differential equation is an algebraic expression which is used to facilitate the solution of the differential equation in question. We can transcribe a nth order differential equation into a nth degree algebraic equation and thus solving for the values of this equation in simpler math.
A characteristic equation, also called an auxiliary equation, must be of the degree equated to the order of the differential equation that is needed to solve. For example, for second order differential equations our characteristic equations would be of second degree. You might have noticed already that this is a clever mathematical trick that allows us to make use of simple math tools to solve for more complicated expressions, the logic behind it relies on the fact that the proportionality of the equations remains the same and thus the results will keep this characteristic, be it an algebraic or a differential equation.
Through this lesson (and at least the next two more) we will focus in trying to find general and particular solutions to second order constant coefficients linear homogeneous differential equations. Such equations will have the form of:
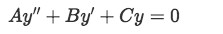
For that, our characteristic equation then will be a second degree algebraic expression with constant coefficients such as:
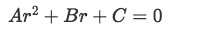
To which we will find its roots in order to find the solution to our differential equation. Thus, notice that since all the characteristic equations we will be working with are good quadratic equation examples, we will have a collection of already known methods to easily find their solutions such as: solving quadratic equations by completing the square, factorization or using the quadratic formula (from which the names "roots" for the solutions came up).
Before we pass into the next section of our lesson, it is important that you are familiarized with the quadratic function in general form and quadratic equations in general, so please go back and check those lessons if you think you need to review them before hand.
What is the discriminant?
The discriminant of a quadratic equation is a particular combination and operation of the constant coefficients found in the quadratic equation which is defined as the operation inside the radical on the general quadratic formula.
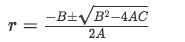
In equation 3 the numbers named A, B and C, are those same constant coefficients found in equations 1 and 2.
In algebra, the discriminant of a quadratic equation is used to know the number of possible solutions you can obtain for such equation. By simply looking at the discriminant, if the result of it is a positive number then we know there will be two possible solutions to the equation, in the same manner, if the discriminant is equal to zero it means there will be one possible solution and if the result from the discriminant is a negative number, then our result will make use of imaginary numbers.
This same usage of the discriminant translates into our methodology to solve differential equations since through it we can quickly know what type of roots does the differential equation have. For second order constant coefficient linear homogeneous differential equations, the resultant characteristic equation and thus, its discriminant, can produce three type of roots, which are: real distinct roots, complex roots and repeated roots.
The condition for each type of root due its discriminant goes as follows:
| Discriminant | Roots |
|
B2−4AC=positive B^{2} > 4AC |
Real and distinct roots |
|
B2−4AC=negative B^{2} < 4AC |
Complex roots |
|
B2−4AC=0 B2=4AC |
Repeated roots |
As you can see from the table, since the discriminant (from its algebraic usage) can tell you that there are two possible solutions to the quadratic equation when it is equal to a positive number, then it means that we can have two possible solutions for r in that case, which end up being our two real distinct roots for the second order differential equation.
For this lesson we will concentrate on those real distinct roots, which refers to the case in which a quadratic equation's solutions are two numbers which we define distinct and real, since they will be real numbers (not imaginary numbers involved) and are different from each other. In other words, we will be studying problems today for those characteristic equations in which you will solve for r, and you will obtain two possible results named r1 and r2and they will be a distinct real number each.
How to find the discriminant
To find the discriminant of a second order linear homogeneous differential equation is a rather simple process that can be done following the next steps:
After you have converted the differential equation into its characteristic equation (from an expression in the form of equation 1, to one in the form of equation 2), identify its constant coefficients A, B and C. The formula for the discriminant then comes from the expression inside the radical in the quadratic formula:
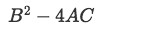
In order to find the value of your discriminant and then determine which type of roots will be the ones you will be working with, you just need to plug the values of the constant coefficients into equation 4 and then take a look at table 1.
When solving second order constant coefficients linear homogeneous differential equations this is always part of your first steps towards a particular solution, since you need to know what type of roots you will be working with in order to decide the path to follow next.
As mentioned before, for this lesson we will concentrate on solving those cases in which you obtain real and distinct roots from your discriminant, but keep going and you will find the other two cases in the next two lessons.
How to find real roots to solve second order differential equations
In order for us to take a look into this methodology completely, we have prepared a few examples fro you to see the process in action, so let us take a jump right away into solving examples:
Example 1:
Find the particular solution to the following differential equation with initial values of: y(0)=2 and y'(0)=1
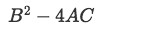
-
We know our general solution for this problem should have the form of:
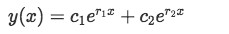
Equation 5: General form of the solution for a second order differential equation -
In order to find out the general solution, we need to find what r1 and r2 are and for that, we need to obtain the characteristic equation of our differential equation. We have practiced this process already in past lessons, in order to simplify the method of solution we have to obtain a characteristic equation, which sort of means that you will be translating a differential equation into a simpler form, in this case, put it as an algebraic expression which is much simpler to solve for, and find its solutions.
For this case we are looking into second order differential equations and so the characteristic equation will have the form of a second degree polynomial equation that can be solved by either factoring out the polynomial in question or just directly using the quadratic formula.
-
A characteristic equation for a second degree polynomial equation has the general appearance of equation 2, and so we can "transcribe" from the differential equation form in equation 1, into the algebraic expression form in equation 2.
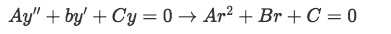
Equation 6: From a differential equation to the characteristic equation -
And so, for example 1 we have that A=1, B=0 and C=-9 and we can now write our characteristic equation for this problem by looking at the equation for example 1:
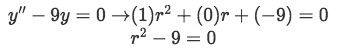
Equation for example 1(a): Obtaining the characteristic equation -
Once you have the characteristic equation, we need to solve for r. For example 1 this turns out to be really simple since we already have that r square is equal to 1, but other cases might not be that obvious and so if you cannot solve for r either directly or with factorization, use the quadratic formula (we will use this in the next examples).
For example one we have that r can have only two solutions which squared result in 9, and so:
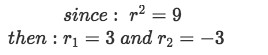
Equation for example 1(b): Solving for r -
And we can now form our general solution for problem in example 1:
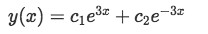
Equation for example 1(c): General solution of the differential equation -
Since we are looking for a particular solution, we need to apply the initial values y(0)=2 and y'(0)=1 to the equation and solve for the unknown constants. For that we must obtain the first derivative of y with respect to x too, and so the process goes as follows:
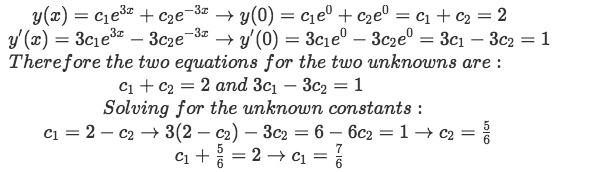
Equation for example 1(d): Applying the initial conditions and solving for the two unknown constants -
And so the particular solution for our differential equation is:
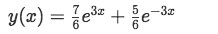
Equation for example 1(e): Particular solution to the differential equation
Now is time for us to list the steps to follow in order to find the characteristic equation for a second order differential equation with distinct real roots:
- Having a second order differential equation, "translate it" into a second degree algebraic polynomial expression with variable r by identifying the constant coefficients A, B and C from equation 2. This is your characteristic equation.
- Find the distinct real roots.
- Since we are solving a second degree polynomial equation as our characteristic equation, we will obtain two possible solutions for r, which are real numbers and distinct from each other, and thus their name.
- You can find these r's sometimes directly by intuition if the resulting characteristic equation is very simple or sometimes you can factorize the polynomial out into two binomials and identify the values of r. But there will be cases in which we cannot directly see the result, and for those you use the quadratic formula to solve for the two possible values.
- Form the general form of the solution for the differential equation by substituting the values of r1 and r2 into equation 5.
- Apply the initial conditions to find the values of the two unknown constant coefficients found in the general solution.
- Compute the first derivative of the general solution, and having both y and y' apply the initial conditions.
- You will end up with two equation for two unknowns: c1 and c2, use these equations to algebraically solve for the unknowns.
- Having found the values of c1 and c2, substitute them into the general solution and in this way, obtain the particular solution for the differential equation.
Having gone through the steps, let us now solve two more examples orderly following the list so you can get more practice at this process:
Example 2:
Find the particular solution of the differential equation below with initial conditions y(2)=1 and y'(2)=4:
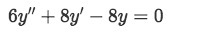
-
Step 1:
Find the characteristic equation:Notice that in this case we did the conversion into the characteristic equation directly. After having practice solving this problems you should be able to do this too, notice that we just passed the constant coefficients from a second order differential equation into a second degree algebraic equation where we have A=6, B=8 and C=-8.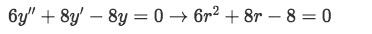
Equation for example 2(a): Obtaining the characteristic equation -
Step 2:
Find the real and distinct roots. For this case this particular equation is not easily factored out and so we directly use the quadratic formula:
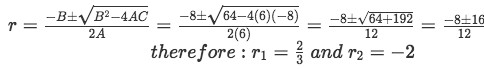
Equation for example 2(b): Solving for r -
Step 3:
Therefore the general form of the solution for the differential equation is:
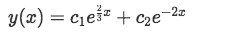
Equation for example 2(c): General solution of the differential equation -
Step 4:
Compute the first derivative of the general solution above and then apply the initial conditions y(2)=1 and y'(2)=4 to y and y' to solve for the two unknown constant coefficients.

Equation for example 2(d): Applying the initial conditions and solving for the two unknown constants -
Step 5:
Substitute the values found for the constant coefficients into the general solution equation and we have the particular solution to our differential equation:

Equation for example 2(e): Particular solution to the differential equation
Example 3:
Find the particular solution to the following differential equation with initial values of y(0)=0 and y'(0)=1

-
Step 1:
Rewrite the differential equation as the characteristic equation: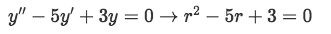
Equation for example 3(a): Obtaining the characteristic equation -
Step 2:
Notice from the above equations that in this case A=1, B=-5 and C=3. Find the real distinct roots using the quadratic formula:
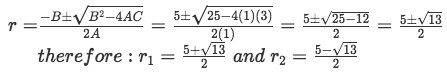
Equation for example 3(b): Solving for r -
Step 3:
Therefore the general form of the solution for the differential equation looks like:
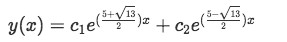
Equation for example 3(c): General solution of the differential equation -
Step 4:
Now we compute the first derivative of the general solution above and apply the initial conditions y(0)=0 and y'(0)=1 to both y and y' to solve for the two unknown constant coefficients:
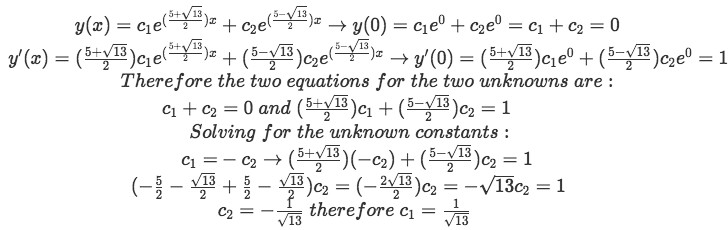
Equation for example 3(d): Applying the initial conditions and solving for the two unknown constants -
Step 5:
Substitute the values found for the constant coefficients into the general solution expression in order to obtain the particular solution to our differential equation:
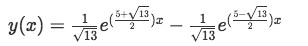
Equation for example 3(e): Particular solution to the differential equation
In the next two sections we will continue with more on solving constant coefficient linear homogeneous second order differential equations. As mentioned before, our characteristic equation will not always produce real and distinct roots as its solutions, there will be times in which we will have to deal with imaginary numbers and so our roots are said to be complex, then there will be other times, when we can only find one root, and soo the roots are said to be repeated. Similar methodology follows these two cases, but still there is a lot of math we have to change, and so, we recommend you to practice and have this first case well settled in your mind, since we will take it as a basis for the next two.
For more examples on real distinct roots that can help you continuing your practice, we recommend you to take a look into these notes on characteristic equations and real distinct roots.
Ay′′+By′+Cy=0
By using the characteristic equation:By using the characteristic equation:
Ar2+Br+C=0
And solving this quadratic will yield two roots, r1,r2. Let's suppose that both r1 and r2 are distinct and real.
So the solution will be:
y1(x)=er1x y2(x)=er2x
Or in full generality:
y(x)=c1er1x+c2er2x
This is the general solution. We can find a particular solution with initial parameters
y(x0)=y0,y′(x1)=y1.
remaining today
remaining today



