Solving differential equations with the laplace transform
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Lessons
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Solving Differential Equations with the Laplace Transform
What is a Laplace transform?
As we have seen in past lessons the Laplace transform definition has the form of:
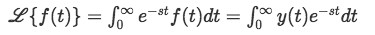
It has been mentioned before on the introductory lesson, that mathematically speaking, we use the term transformations when referring to clever tricks in math that will allows to change a problem from higher level methodology into something simpler, such as algebra.
This is exactly the case for our lesson of today, where we will use the Laplace transformation in order to decompose a higher order linear differential equation, separate its terms, simplify, and then work them through to obtain an expression for the implicit solution of the differential equation.
In order to calculate such result, we will first compute the two main equations that will be used throughout the process, these equations which we recommend to learn and keep them at hand, are the ones shown in equation 6. Afterwards we will explain the calculations in a list of steps and we will finish by solving a few examples on the topic.
Solve differential equation using Laplace transform:
So we have already had an introduction to the Laplace transform and even a lesson on how to calculate Laplace expressions by a simple method of comparison. Now is time to see how these transformations are helpful to us while solving differential equations.
In reality, we need both Laplace transforms and Inverse Laplace transforms in order to find the solution to an ordinary differential equation, the trick is to apply one first (which will allow us to change the differential equation to an expression containing only y's), simplify the equation as much as possible and then reverse it by taking the inverse transformation to solve to y.
This process will be aided by the Laplace transform table shown below:
Such table containing common Laplace transforms will allow us to once again solve difficult problems by comparison with the equations contained on the table. If you need a review on how to use this table do not forget to check the lesson on calculating Laplace transforms.
But the most important part of the process of solving differential equations with a Laplace transform comes from a derivation of equation 1 shown in the last section, this is, when we apply the Laplace transform formula to the derivative of y.
From the definition of Laplace transform given in equation 1, you can see that the represented transformation is of a function of t, this is because we usually define y=f(t) or "the y function is in terms of t, and therefore is a function of t". Since we will be solving "differential" equations, this means we will be working with derivatives of y, and so let us work through the Laplace transform of the first derivative of y:
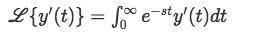
For which we need to work through using integration by parts:
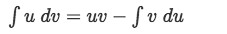
Thus:
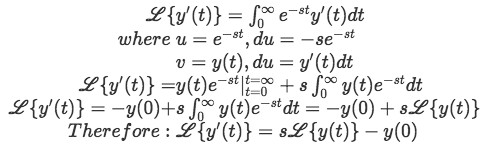
Using the definition we just found for the Laplace transform of the derivative of y, we can continue to obtain the Laplace transformations of higher derivatives of y, let us take a look to the next one:
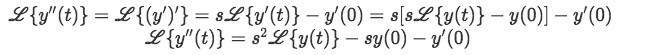
And so, the equations we will be using to solve differential equations with the Laplace transform come to be:
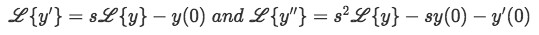
The trick for this process, and which makes it very simple to follow, is that you will only be using the Laplace transform to decompose the differential equations into their different terms and simplify them; once the Laplace transform has done this, you will take the inverse transformation to go and retrieve y(t). The description and step by step process is given in the next list:
- Take the Laplace Transform of the differential equation
- Use the formula learned in this section to turn all Laplace equations into the form L{y}. (Convert all things like L{y''}, or L{y'})
- Plug in the initial conditions: y(0), y'(0) = ?
- Rearrange your equation to isolate L{y} equated to something.
- Calculate the inverse Laplace transform, which will be your final solution to the original differential equation.
Now you are ready to work through the next Laplace transform problems with answers. We suggest you to copy the problem to your notebook and try to solve it on your own, then check if your result agrees with the answer given.
Laplace transform examples
For this section, we will be working through two Laplace transform examples, we recommend you to have the table of Laplace transforms at hand and the set of instructions written above, since you will be using them for both problems.
Example 1
Solve the initial value differential equation with initial values y(0)=2 and y'(0)=6
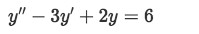
-
Step 1:
First we apply the Laplace transformation of the differential equation and simplifying following the property of linearity: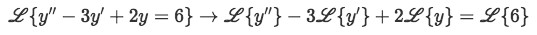
Equation for example 1(a): Applying the Laplace transform to the differential equation -
Step 2:
Substitute equation 6 into the equation above to turn all Laplace equations into the form L{y}: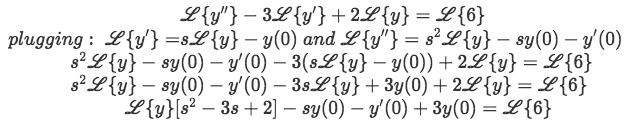
Equation for example 1(b): Substituting the known expressions from equation 6 into the Laplace transform -
Step 3:
Insert the initial condition values y(0)=2 and y'(0)=6.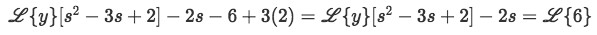
Equation for example 1(c): Applying the initial conditions to the problem -
Step 4:
Rearrange your equation to isolate L{y} equated to something.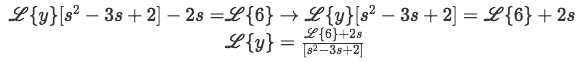
Equation for example 1(d): Rearranging the equation to solve for the Laplace transform of y -
Step 5:
Now in order to calculate the inverse Laplace transform we must first simplify the expression we have for the Laplace transform in a way that we can use the method of comparison with table 1 in order to find the solution.
For this particular expression the first thing we have to do is to substitute the Laplace equation of 6 found in the right hand side to its appropriate value. For that, we use the second column of table 1 where we can find that if f(t)=1 then L{f(t)}=L{1}=s1. Therefore L{6}=s6 is just the Laplace transform of 1 multiplied by 6, and we substitute that in our expression found so far for the Laplace transform of y: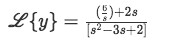
Equation for example 1(e): The Laplace transform of y in terms of s Now we use algebra to manipulate the equation above until we get an expression that is easy to relate to the solutions for Laplace transforms in table 1. We start by multiplying the numerator in the right-hand side by 1=ss and then we factorize the denominator into a multiplication of binomials.
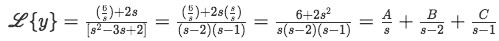
Equation for example 1(f): Algebraic manipulation of the Laplace transform So our Laplace transform has been converted into an expression containing the addition of three fractions, which in turns resembles much more the notation of the expressions found in the second column of table 1 and so it seems we are on our way to find the solutions. Before we can do that, we need to know what A, B and C are, and so, we solve this found equation using the method of partial fractions:
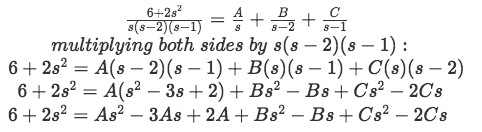
Equation for example 1(g): Obtaining an identity equation to find coefficients A, B and C Which is an identity equation (meaning is true for any value of s), thus for convenience we start by setting s=0.
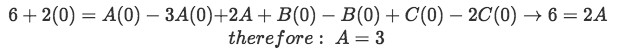
Equation for example 1(h): Solving for coefficient A We plug our newly found value of A into the final equation for example 1(g) and then we set our s=1 to find the next coefficient.
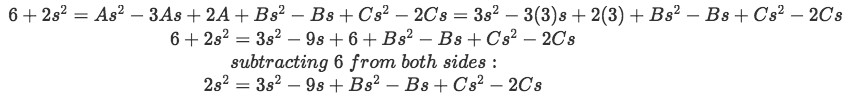
Equation for example 1(h): Plugging the found value of A into the equation Now setting s=1:
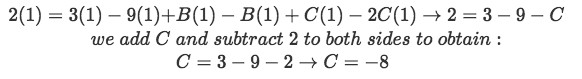
Equation for example 1(i): Solving for coefficient C Once more, we substitute the found value of C, but now into the found equation for example 1(h) and then we set s=2 to find B:
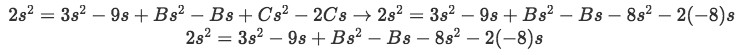
Equation for example 1(j): Plugging the found value of C into the equation And setting s=2:
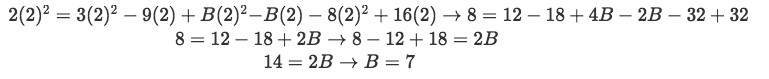
Equation for example 1(k): Solving for coefficient B Now that we have finally found the values for the three unknown coefficients A, B and C we can go back to our equation for example 1(f) and plug them into it:
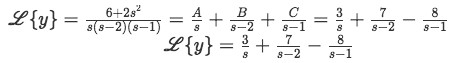
Equation for example 1(l): Finding the simplified notation for the Laplace transform Having this very nice expression for the Laplace transform we can finally apply the inverse Laplace transform to the whole expression and find the equation for y (solution of the initial second order linear differential equation).
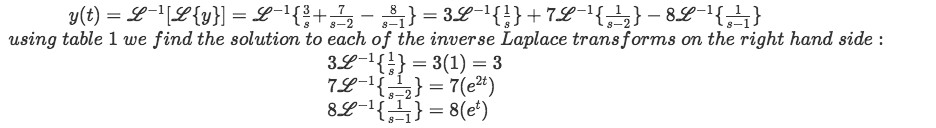
Equation for example 1(m): Solving all the inverse Laplace transforms involved on y using table 1. And so we put together all of the results from the inverse Laplace transforms to find the final solution for y:
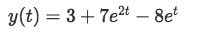
Equation for example 1(n): Final solution for the differential equation
This particular example could also have been solved using the method of undetermined coefficients. We invite you to try it out in your free time if you please.
Example 2
Find the solution to the second order linear differential equation using the initial values y(0)=3 and y'(0)=7
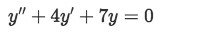
-
Step 1:
We start by taking the Laplace transform of the differential equation and simplifying due linearity:Before we continue with the next step, notice how the expression on the right-hand side is equal to zero. The Laplace transform of 0 is easily thought as the Laplace transform of a constant or variable being multiplied by zero, and thus resulting in an expression similar to: L{0×c}=0L{c} or L{0×y}=0L{y}=0 another way to see it is that if your function is equal to zero: f(t)=0 then L{f(t)}=0 and thus, the Laplace transform of zero is just zero.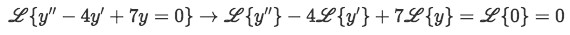
Equation for example 2(a): Applying the Laplace transform to the differential equation -
Step 2:
Substitute equation 6 into the equation above to turn all Laplace equations into the form L{y}: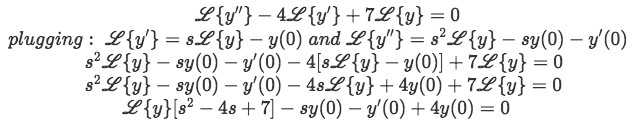
Equation for example 2(b): Substituting the known expressions from equation 6 into the Laplace transform -
Step 3:
Insert the initial condition values y(0)=3 and y'(0)=7.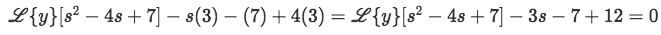
Equation for example 2(c): Applying the initial conditions to the problem -
Step 4:
Rearrange your equation to isolate L{y} equated to something.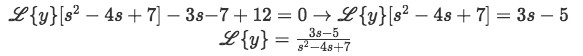
Equation for example 2(d): Rearranging the equation to solve for the Laplace transform of y -
Step 5:
Once more, we must simplify the expression found in equation for example 2(d) into an equation that we can solve by taking its inverse Laplace transform and comparing with our table 1 to obtain the results. Notice that in this case, we cannot just factorize the polynomial in the denominator, and if we try to solve it using the quadratic equation we end up with a square root of a negative number, which makes this method unviable.Therefore we have to be clever to algebraically manipulate this equation in order to use the table alone to solve it. Let us look at the process step by step:
Having the expression for the Laplace transform of y:
If we pay attention to the denominator in the right hand side of the equation we can conclude that there should be a way to factorize part of that expression and just add a constant to make the complete result agree with what we have. And so, let us look for equations in the second column of table 1 that have a mix of the product of a binomial plus (or minus) a constant in the denominator, the formulas that fit into this description are: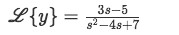
Equation for example 2(d): Rearranging the equation to solve for the Laplace transform of y 
Table 2: Equations that we could possibly use to solve equation for example 2(d) So we obtain as our possibilities the trigonometric functions of sine and cosine multiplied to the exponential, and their hyperbolic counterparts. We will dismiss the hyperbolics as possibilities due to their condition of s-a>|b|, and so we are left with the solutions containing sine and cosine.
Thus we need to manipulate the expression in the denominator in our equation for example 2(d) to resemble the denominators found in the equations I and J from table 2.
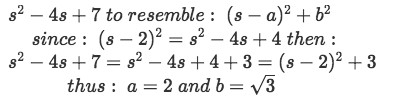
Equation for example 2(e): Manipulation of the denominator found in the Laplace transform Therefore we rewrite our Laplace transform equation:
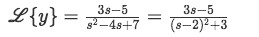
Equation for example 2(f): Rewriting the Laplace transform If we apply the found values of a and b to the formulas I and J from table two we have:
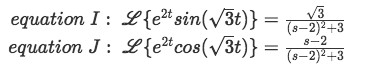
Equation for example 2(g): Substituting the values of a and b into equations I and J Notice we are getting there, our Laplace transform (equation for example 2(f)) is already looking very similar to the equations above, then now we look into the numerator of the right-hand side of our equation for example 2(f) so we can manipulate it in a way to use equations I and J on them:
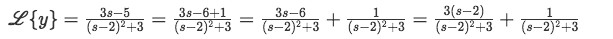
Equation for example 2(f): Rewriting the Laplace transform And now is obvious how we can rewrite the Laplace transform using the expressions found in equation for example 2(g):
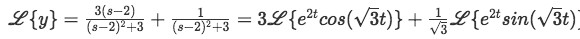
Equation for example 2(g): Final expression for the Laplace transform Now we just apply the inverse Laplace transform to everything:
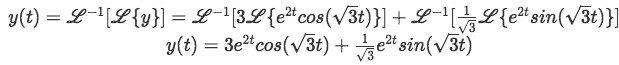
Equation for example 2(h): Final solution for the differential equation
It is important to note that we have already gone through this problem before, if you want to see the video with the full explanation on how to solve it (to complement what is written on this lesson), you can go ahead and check the lesson on the Inverse Laplace Transform on the video for lesson 3b.
As we wrap up this lesson, remember that this particular topic has been explained and extended through the last 3 lessons and so, if at any point in time you feel confused about something on the problems shown above, we suggest you to go back and review the Laplace transform properties, formulas, and definitions we have seen before throughout the StudyPug past sessions. Also, consider these other Differential equations notes as reference throughout all of them.
We can actually use Laplace Transforms to solve differential equations
And so,
And in full generality:
Which can be used to make high level order differential equations much easier to solve, just take the following steps:
1. Convert the differential equation into a Laplace Transform
2. Use the formula learned in this section to turn all Laplace equations into the form L{y}. (Convert all things like L{y''}, or L{y'})
3. Plug in the initial conditions: y(0), y'(0) = ?
4. Rearrange your equation to isolate L{y} equated to something.
5. Calculate the inverse Laplace transform, which will be your final solution to the original differential equation.
remaining today
remaining today



