Interval of validity
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
- Determining Intervals of Validity
For each of the following differential equations, the corresponding slope field is provided.
Sketch the solution for each differential equation with the specific initial conditions given. What is the interval of validity? - In the section to do with Bernoulli Equations the solution to the differential equation:
dxdy+x1y=y3
with initial condition y(21)=1 was found to be:
y=2x1
Plot out this solution and explicitly give its interval of validity. - Solve the following differential equation:
dxdy=−2xe−y
With initial conditions y(1)=0.
What is the interval of validity for the solution? - Solve the following differential equation:
dxdy=4xy2
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Interval of Validity
What is an interval in math
During this lesson we will be learning an important characteristic of first order differential equations called the interval of validity, we will even see how sometimes this characteristic can be easily inferred without even having to find the solution to the equation itself. But before we continue to describe such characteristic is important to understand the language we use to describe it, and so we will first learn what is an interval and how do we define valid or not valid.
Let us first define intervals in terms of real numbers and so, we can call a given set of real consecutive numbers, with one of them being the beginning and another one the end, an interval in which certain values exist. In this case, any number that can be found between the beginning and end values is said to be part of this set.
In simple words, a quick interval math definition would mean just a range of consecutive values that form a set. For this lesson we will talk about intervals of functions which will refer to the range of values found in a function (or a piece of a function) as long as it is continuous.
Now let us take a look into the validity definition. For an argument, in the case of mathematics a result or value, to be valid means that we can logically conclude the given scenario will return such conclusion. In other words, by analysing a certain problem (this can be done without finding the solution yet) we can conclude that a certain result is valid just because given the characteristics of the problem such result is logically possible. If the claimed result has no possibility of occurring under such conditions or has no logical basis, then this answer is said to be invalid.
In this way we put together the definitions of interval and validity and we can say that for any given interval any value found inside its range will be a valid value for the interval. This is not the definition of interval of validity, but is still big part of the logic behind this terminology, we will look into a precise definition in the next section of our lesson.
Last but not least, notice how validity depends on the initial conditions of the given scenario, this is an important detail when working on differential equations since the initial condition of the problem will give you information needed to find an interval of validity.
Definition of interval of validity
For a given differential equation with an initial condition, the interval of validity is the range of values of the independent variable at which the solution to the equation is valid for such initial condition.
We call the notion of the interval of validity as the existence and uniqueness theorem since it describes how the largest continuous range of a function where a unique solution is definite to exist can be known even when the solution to the differential equation may not be possible to be known. This is important because it means that we can have an idea of the behaviour of a function and an approximation of what it will look like or turn out to be even when is not possible for us to know its true values.
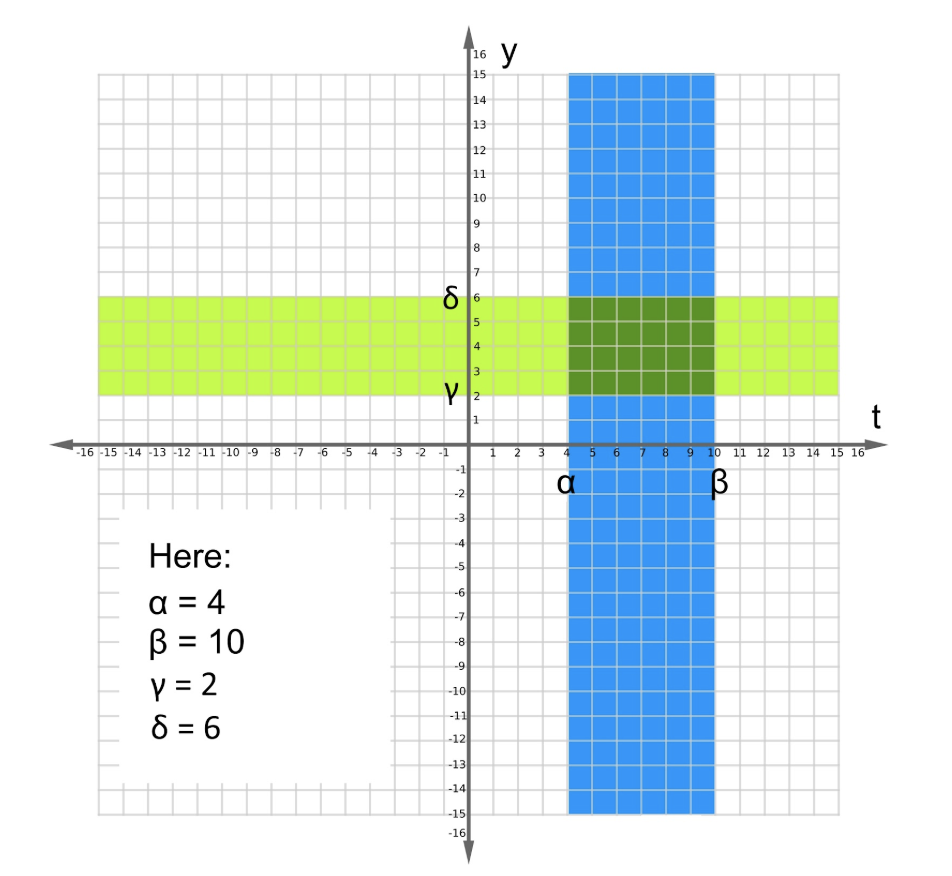
This theorem, also known just as the uniqueness theorem, says that when having an initial value such as y(t0)=y0 we can be sure of the existence of a unique solution in the interval α<t<β where the condition exists, for a linear differential equation of the form:
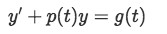
Therefore, linear differential equations in the form of equation 1 are called uniqueness theorem differential equations. But why uniqueness and what is a unique solution? A unique solution means that in the certain range found, for those functions (p and g) and for a particular value of x in them, there is only one possible value of y, and so, that is why the interval of validity depends on the initial condition. But take a look at the figure below and notice how for a linear equation, the interval of validity depends only on the values of t, so the important part of the initial condition is the value of to.

Since we are positive we will find the answer to the equation in the found interval, we can also call the interval of validity as the interval of existence.
And this second name: "interval of existence" makes more sense to our next definition. The theorem of the interval of validity also has a form for nonlinear differential equations, which although a little bit more impractical, is still important to know the characteristics of different functions. Mathematically written, this second theorem says that for a given equation such as:

With initial condition of y(t0)=y0 , if f(t,y) and ∂y∂f are continuous in a rectangular range with boundaries α<t<β and γ<y<δ which contains the initial condition, then a unique solution for the differential equation exists on that range.
Notice that in this case, the interval of validity depends on both t and y, and therefore, we need to find y before we can identify the interval of validity. This also means that there could be different possible values of y for each value of t in other intervals, and thus, the name "interval of existence" takes precedence sometimes for these type of problems, but remember, as long as you pick the interval including the initial condition the uniqueness consideration remains. The theorem describing the conditions for such problems can also be called the Picard-Lindelof theorem or the Cauchy-Lipschitz theorem and as mentioned before, it still keeps the uniqueness consideration by focusing ONLY on the rectangular range given by the four points α,β,γ,δ and in which there is only one possible value of y for the particular value of t.
And so, for nonlinear differential equations we will not only need an initial condition, but we will also have to solve the differential equation first and find its exact solution in order for us to identify the largest interval in which f(t,y) and the partial derivative of f with respect to y are continuous, same interval which contains the initial condition and in which the solution exists, and thus call it the interval of validity.
As you can see, in the case of nonlinear differential equations the theorem truly is "impractical", because this theorem's form is not good enough for us to use and find an interval of validity without solving the problem first. In this case the theorem it is more like a "checking" tool in which you will have to solve the equation completely on your own (not very difficult, you will see a few examples later) and then check if the problem meets the conditions of the theorem and declare the interval of your solution as valid.
Confusing? It can be, but worry not, we will be finding the interval of validity for both cases: linear and nonlinear differential equations, and you will see for yourself how this works.
Interval of Validity for linear first order differential equations
For us to easily see how to identify an interval of validity for a linear function, let us go directly into our first example, we will then list the steps of the whole process and work on a few more examples so you can get more practice.
Example 1:
Having the linear differential equation below with the initial condition: y(0)=-1
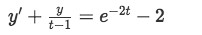
-
Taking a look to equation 1, we start by identifying the functions p(t) and g(t):
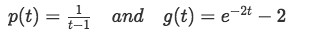
Equation for Example 1(a): Identifying functions p(t) and g(t) -
Notice that the function g(t) is continuous for all real numbers while function p(t) is not continuous if the value of t is 1 since a division by zero is undefined. Therefore the intervals of continuity (those where both functions are continuous) are:
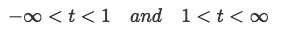
Equation for Example 1(b): Intervals of continuity -
Since the initial condition is located where t=0 and in this case the validity of the differential equation depends only on t (the independent variable), then the interval of validity for the linear differential equation is:
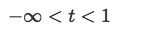
Equation for Example 1(c): Interval of validity for the linear differential equation
Having solved our first problem, let us now list the steps to find the interval of validity for a linear differential equation:
- Identify p(t) and g(t)
- Find out where p(t) and g(t) are not continuous
- List the intervals where both p(t) and g(t) are continuous
- From the listed continuity intervals identify the one containing the initial condition, this is your interval of validity.
- Prove it! (OPTIONAL): Find the solution to your differential equation and check how you can find it within the range of your found interval of validity.
As you can see this process is very easy! Sometimes the equation can be so simple that you may even be able to obtain the answer right away thanks to your empirical knowledge and logic. So keep on practicing to develop that empirical sense that will help you resolve these problems faster, for that, let us continue with two more examples:
Example 2:
Starting out with the linear differential equation below and the initial condition: y(0)=-5
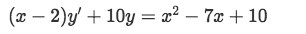
Notice that in this case the independent variable is x and not t.
-
Step 1:
Now we rearrange the differential equation and find the functions p(x) and g(x):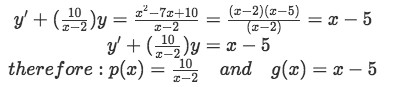
Equation for Example 2(a): Identifying functions p(x) and g(x) -
Step 2:
Notice that p(x) is not continuous at x=2 since it would be a division by zero: 10/0=undefined and once again, the function for g(x) is continuous everywhere. -
Step 3:
So we list the intervals of continuity, and since g(x) is continuous everywhere then we just pay attention to the ones where p is also continuous and list them, since g will be continuous there as well.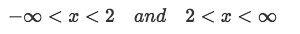
Equation for Example 2(b): Intervals of continuity -
Step 4:
From the listed continuity intervals we know that the initial condition is found at x=0, therefore your interval of validity is: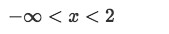
Equation for Example 2(c): Interval of validity for the linear differential equation
Example 3:
Let us work in our last example for interval of validity for a linear differential equation. Using the initial condition y(0)=2 find the interval of validity of the equation:
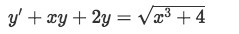
-
Step 1:
We rearrange the differential equation and find the functions p(x) and g(x):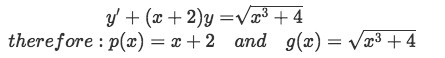
Equation for Example 3(a): Identifying functions p(x) and g(x) -
Step 2:
In this case the function for p(x) is continuous for all real numbers and so we pay attention to the spots where g(x) is not continuous. Since the square roots of negative numbers are not real, we find values of x where g becomes a square root of a negative number. Therefore g(x) is not continuous when x3<−4 , but is continuous for all numbers where x3 is equal or bigger than -4. -
Step 3:
So we list the intervals of continuity where both equations are continuous. For this, we need to solve for x when g(x)=0 so we can find the starting point of its continuity: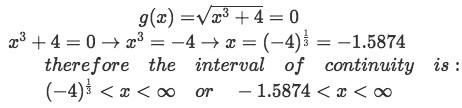
Equation for Example 3(b): Finding the interval of continuity -
Step 4:
Since this is the only interval where both functions are continuous and we can find the initial condition within it, then that is our interval of validity: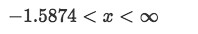
Equation for Example 3(c): Interval of validity for the linear differential equation
Interval of Validity for nonlinear first order differential equations
Let us take a look into example 4 for our first example of the interval of validity of a nonlinear first order differential equation. We will list the steps afterwards and finish the article with a last example for this section.
Example 4:
In the past section, which talks about Bernoulli Equations,we found the solution to the next nonlinear differential equation with initial condition y(21)=1:
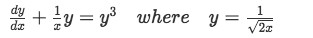
Let us plot that solution and solve for its interval of validity:
- In this case the problem asks us to plot the solution (y variable) so what you can do by hand is use the formula for y and construct a table with two columns, one for x and one for y. On this table you select the values of x that you want to work with and compute the value of y for each s. We recommend you to select a range of x that covers from a few negative values to a few positive ones, make the step size between these values as small as you can and in this way be able to get the shape of the function as you graph your values.
-
This is a simple procedure you have done before, and for that we have just graphed y in the next figure: (If you have any issues graphing y do not forget to check out the videos on top of this lesson, in there you can see the step by step process of getting this graph).
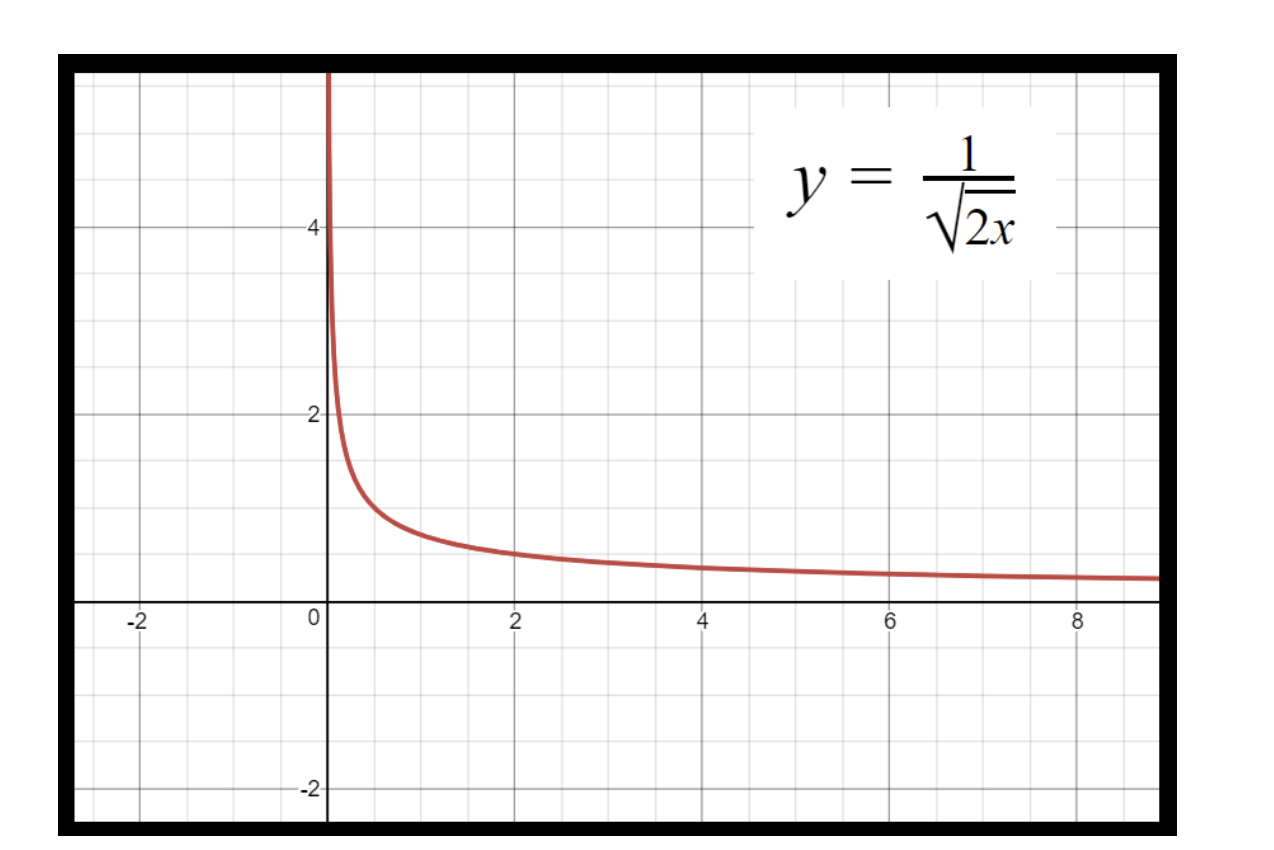
Figure 3: Graph of y for the equation for example 4. - From the graph you can quickly see that the interval of validity for this differential equations MUST be between o to positive infinity since that is the only region where the function y is continuous and that is where the unique solution according to the initial condition is located. But could you have found this without doing the graph? YES! Let us look at the mathematical logic behind this graph that would give us the answer without the picture representation of the function.
-
If we take a look at the formula for y, we can notice two things:
- x cannot be zero because that would give an undefined result while trying to divide by zero.
- x cannot be negative, because that would not give a result in real numbers.
- Hence the only continuous interval of y left is 0<x<∞ , and since the initial condition says that when x=21,y=1 we can plainly see that this point (21,1) is located inside the continuous interval and so this continuous interval is the interval of validity!
Having seen this simple example, let us list the steps to follow to find the interval of validity for a nonlinear differential equation:
-
Find the solution to the differential equation.
- You can usually find the solution to these types of equations through the method of separable equations.
- Use the initial condition to find the value to any unknown constant that may come up.
- OPTIONAL: construct the graphic representation of the function y.
- Identify the points at which y is not continuous.
- List the intervals at which y is continuous.
- The interval containing the initial condition is the interval of validity.
Let us work through our last example, and in this case we will solve it completely: from finding the solution to the nonlinear differential equation to plot and then follow all the steps to find the interval of validity.
Example 5:
Solve the nonlinear differential equation below with the initial condition y(1)=0 and then find the interval of validity of its solution:
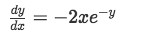
-
Step 1:
We find the solution to the differential equation using the method of separable equations:After finding y we find the value of any unknown constants left using the initial condition which says that when x=1, y=0, then: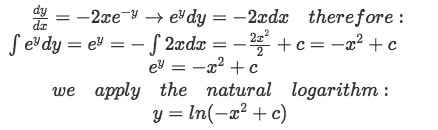
Equation for Example 5(a): Finding y through the separable equations method And so our solution for the differential equation is: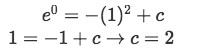
Equation for Example 5(b): Solving for the unknown constant 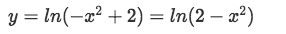
Equation for Example 5(c): Solution to the differential equation -
Step 2:
Construct the graphic representation of the function y:In this case, although we can easily see there is only one interval that is continuous and which contains the initial condition, is difficult to observe the values at the edges of the interval from the graph, so let us pass to the mathematical calculation to find out the points at which y is not continuous to obtain the exact values of the edges.
Figure 4: Graph of y for the equation for example 5. -
Step 3:
Identify the points at which y is not continuous. For that we take a look at y again:Notice that when x2=2 then we obtain y=ln(0) which is impossible to obtain since this would mean that there is a power at which we could elevate e and obtain zero as a result. So ln(0) is impossible, or undefined if you will and so, y is not continuous at the value of x which results in x2=2. In this case, there are two values that result in x2=2, and these are the positive and negative square roots of two. Therefore, these two values are our edges of the continuous interval seen in the graph! For any value bigger than the positive square root of two and smaller than the negative square root of two, we end up trying to compute the natural logarithm of a negative number which is undefined. So we say y is continuous in the interval −2<x<2 and nowhere else, and therefore, this is the interval of validity of the equation.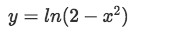
Equation for Example 5(c): Solution to the differential equation
As always, if you want to do some further reading and studying on this topic, we recommend you to visit these Differential equation notes focused on intervals of validity where you can find a few more problems and explanations.
An interval of validity is the range in which a solution to our differential equation is valid. The equation must not have any 'holes' or 'breaks' in it and it must contain the initial condition.
We can use our initial condition to find what our exact solution is, and find out what is our interval of validity
Theorem:
For an Initial Value Problem (IVP) of the form:
y′+p(x)y=g(x)
With initial value: y(x0)=y0
If both p(x) and g(x) are continuous functions on the interval α < x < β, with our initial condition x0 being within this interval, then there exists a unique solution to the IVP above.
remaining today
remaining today





