Determining trigonometric functions given their graphs
All in One PlaceEverything you need for better grades in university, high school and elementary. | Learn with EaseMade in Canada with help for all provincial curriculums, so you can study in confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
0/3
Examples
Lessons
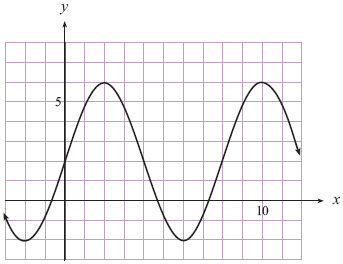
- For the following graph, write an equation (with the smallest phase shift) in the form of:
(i) y = a sin b(x - c) + d
(ii) y = - a sin b(x - c) + d
(iii) y = a cos b(x - c) + d
(iv) y = - a cos b(x - c) + d - A sinusoidal curve has a minimum point at and the closest maximum point to the right is . Determine an equation of this curve.