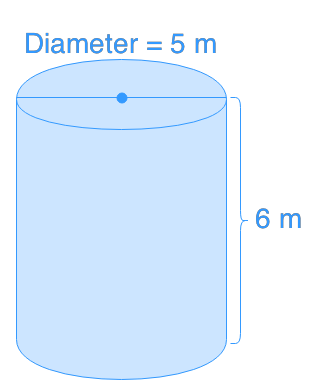
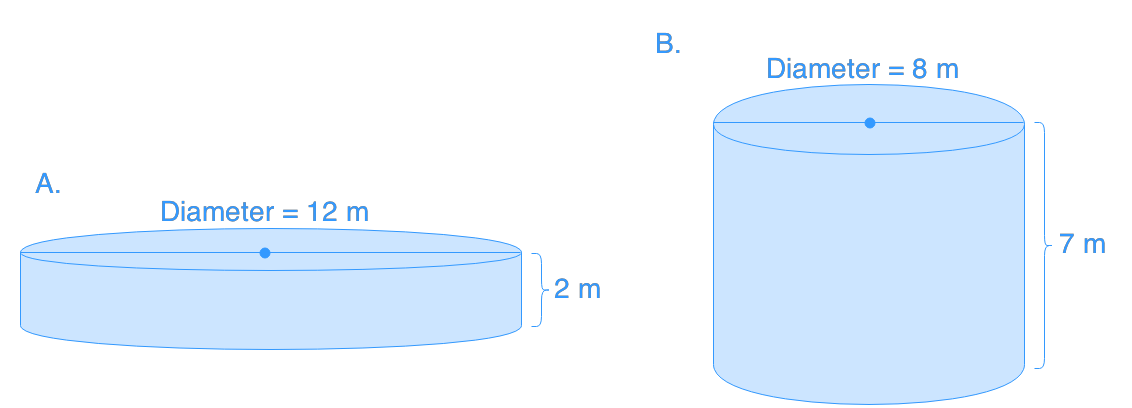
Surface area of cylinders
All in One PlaceEverything you need for better grades in university, high school and elementary. | Learn with EaseMade in Canada with help for all provincial curriculums, so you can study in confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |