Interactive Grade 8 Math Help and Practice
Improve Grade 8 Math skills with practice questions, video lessons, and more!

Learn Faster with StudyPug

All in One Place
Everything you need for better grades in university, high school and elementary.
Learn with Ease
Made in Canada with help for all provincial curriculums, so you can study in confidence.

Instant and Unlimited Help
Get the best tips, walkthroughs, and practice questions.
Grade 8 Math Topics
Representing Data
Ratios, Rates, and Proportions
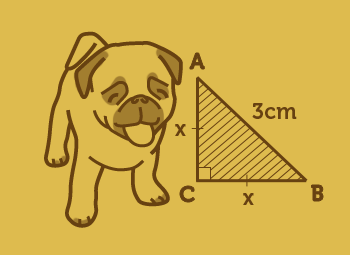
Pythagorean Theorem
Percents
Surface Area
Volume
Integers
Linear Relations
Linear Equations
Probability





































The Popular Learning Tool Trusted by Parents and Teachers
2
Videos
Remaining Today
5
Practice Questions Remaining Today
Get more free views and practice!






