Determining non-permissible values for trig expressions
All in One PlaceEverything you need for better grades in university, high school and elementary. | Learn with EaseMade in Canada with help for all provincial curriculums, so you can study in confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Determining Non-Permissible Values in Trig
When dealing with trigonometric functions and expressions, oftentimes we will encounter and be asked to solve for trig values for which an expression is "non-permissible" – that is, our answer would be undefined. This most often occurs when trig values equal zero, for example sin0. These values are also called non-permissible values when they result in an expression that is undefined. Below is a trig values chart that has the exact values of trig functions for sine, cosine, and tangent.
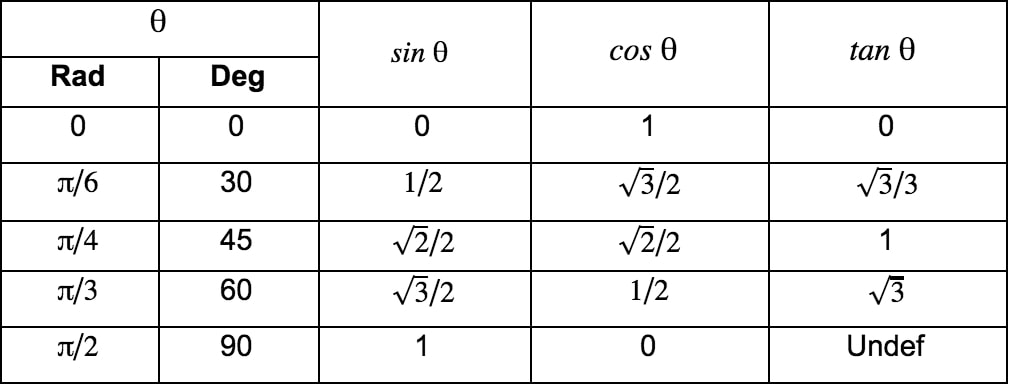
NOTE: This chart just gives the values for sine, cosine, and tangent in the first quadrant using the common reference angle. If you recall, these values will vary in their sign (+/-) depending on which quadrant the angle is in. We can use the acronym ASTC (All Students Take Calculus) to help us to remember which trig ratio is what in each quadrant:
For a review of some of these concepts in a more detailed video, check out our clips on the reference angle, the exact values of trig functions, and All Students Take Calculus. As well, before we can identify the non-permissible values, simplification steps will often need to be made. The next few sections cover the most important trig identities.
Pythagorean Identities:
Though this should be second nature to you now, it is important to make sure you have a firm grasp of these most basic identities.
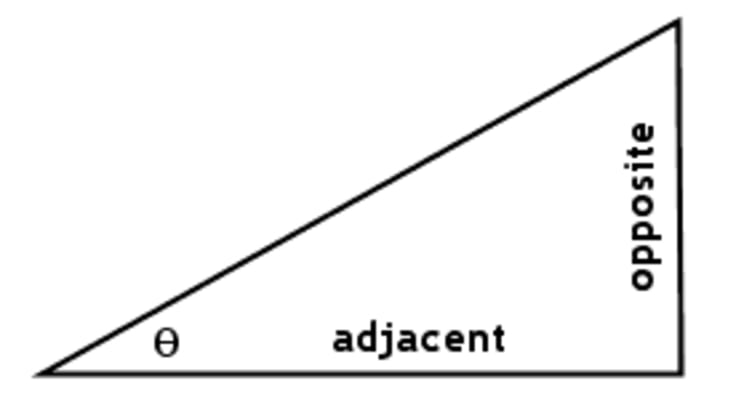
In order to understand trigonometric ratios, let's first look back on some basic trigonometry principles. First, the Pythagorean Theorem with right triangles, and SOHCAHTOA. If you recall, we can use the Pythagorean Theorem (a2+b2=c2) to solve for unknown side lengths of right triangles, and we can use SOHCAHTOA to find missing angles. Below are the formulas we get from SOHCAHTOA, as well as an image to help you visualize it:
Quotient Identities:
In trigonometry, quotient identities refer to trig identities that are divided by each other. There are two quotient identities that are crucial for solving problems dealing with trigs, those being for tangent and cotangent. Cotangent, if you're unfamiliar with it, is the inverse or reciprocal identity of tangent. This identity will be more clear in the next section. Below, this image covers the two fundamental identities you must know when it comes to quotient identities.
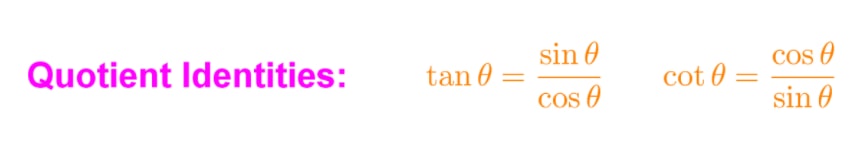
Reciprocal Identities:
Have you ever wondered if there was an easier way of dealing with the trigonometric expressions such as sin−1x? It turns out, there is. In trigonometry, reciprocal identities or inverse identities cover this base. Instead of writing sin−1x or sinx1 , we can use the reciprocal identity cscx instead. Cosecant (csc), secant (sec), and cotangent (cot) are extremely useful identities, and you will use them extensively as you progress with mathematics into pre-calculus and calculus. Therefore, it is quintessential that you memorize and understand all of these identities. The image below covers what you must know.

How to Find Point Discontinuity:
Now that we have gone over the most important identities used to simplify trig expressions, we can focus in on how to find points of discontinuity. Of course, the best way to learn this is to do a couple of example problems:
Example 1:
Find the point(s) of discontinuity for the following trig expression:
Step 1: Find the Expression of Discontinuity
As mentioned earlier, non-permissible values occur when an expression is undefined, most often when the denominator equals zero. In this case, let's make the denominator equal to zero and simplify.
Step 2: Solve for Values of x
Now we need to solve for x to find which values of the variable result in sinx being equal to −21. According to ASTC, sine is negative in the third and fourth quadrant.
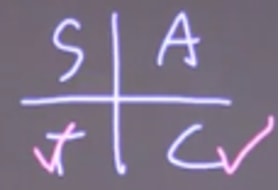
Next, because we know that sin30 (or sin6π) is equal to 21, all we need to do is use this reference angle in each of these quadrants.
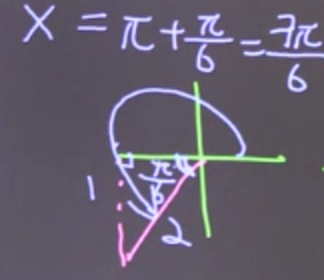
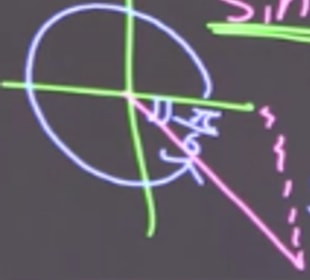
This leaves us with our answers, which are our points of discontinuity:
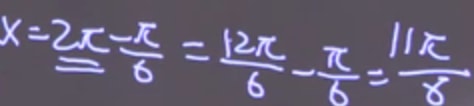
Example 2:
Find the point(s) of discontinuity for the following trig expression:
Step 1: Simplify
Again, as mentioned before, we often need to use trig identities to simplify our expressions before we go solving for non-permissible values. In this case, we use reciprocal trig identities to simplify and find the expression for the points of discontinuity. We will find two expressions for this in this particular example.

Step 2: Solve for Values of x
Again, now we need to solve for x to find which values of the variable result in cosx being equal to 0 or 1. In this case, we don't need to use ASTC because we can easily find these values through the graph of cosine.
This leaves us with our final answers, which are our points of discontinuity:
And that's all there is to it! For another example, check out this great one on the web here. As well, for further study, see our videos on how to find point discontinuity, the vertical asymptote, and the derivative of trigonometric functions.
Basic Concepts
remaining today
remaining today



