Conics - Hyperbola
All in One PlaceEverything you need for better grades in university, high school and elementary. | Learn with EaseMade in Canada with help for all provincial curriculums, so you can study in confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
0/1
Intros
Lessons
- Hyperbola:
horizontal hyperbola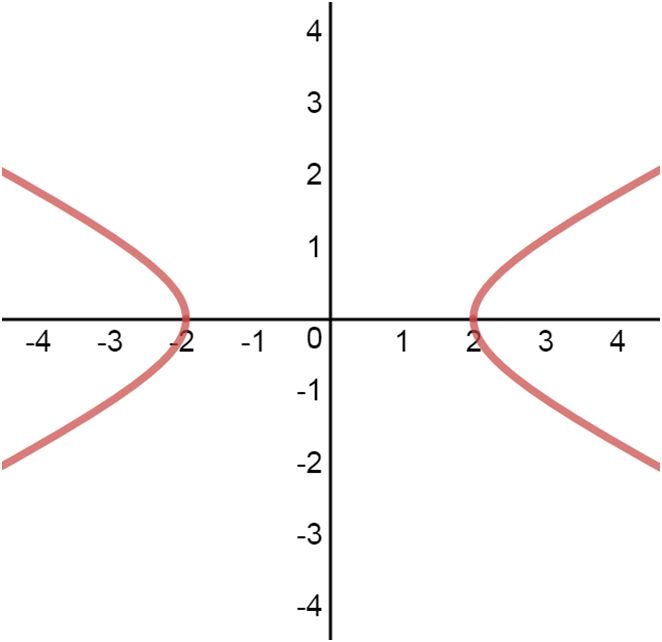 vertical hyperbola
vertical hyperbola
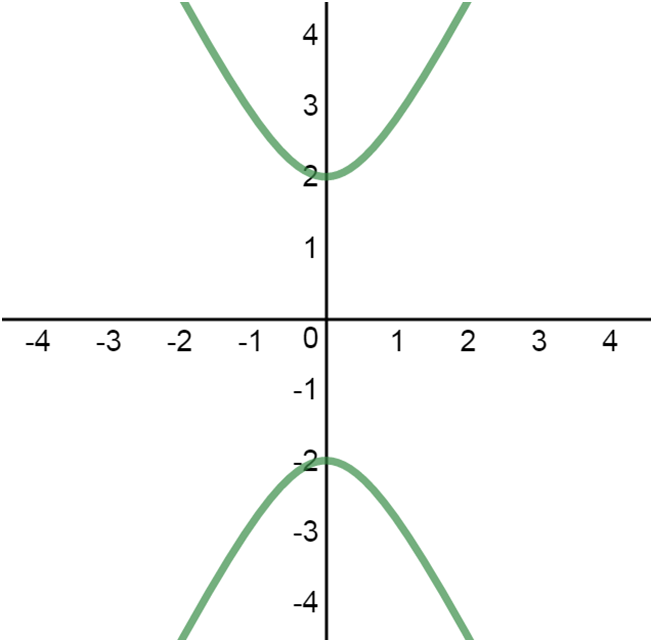
• Graph looks sort of like two mirrored parabolas, with the two "halves" being called "branches".
• "Vertices" are defined similarly to the way of a "vertex" is defined for a parabola.
• Just as the focus for a parabola, the two foci for a hyperbola are inside each branch.
• The line connecting the two vertices is called the "transverse axis".
0/8






