Factoring trinomials
All in One PlaceEverything you need for better grades in university, high school and elementary. | Learn with EaseMade in Canada with help for all provincial curriculums, so you can study in confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
- Factor:
- Factor:
- Factor:
- Factor:
- Factor:
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
How to factor trinomials
Trinomials are algebraic expressions that has three terms in it. Quadratic trinomials are in the form of ax2 + bx + c, and the a, b, and c all stands for a number.
In order to factor trinomials, you'll have to work to find two numbers that will multiply to equal the "c" from the quadratic form above, and also add up to equal "b". These are the steps for the easier questions where the first "a" is equalled to 1. For harder problems, "a" will be a number that is not one. You'll have to first multiply "a" and "c", and then find factors of the product "a*c" that also add up to "b".
We'll explore this with example questions to demonstrate how to factor trinomials.
Question 1
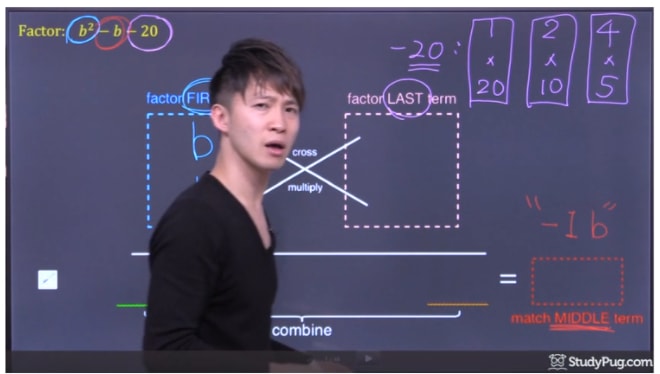
Factor: b2−b−20
Solution:
In this example, we are going to use the "cross-multiply, then check" method to factor the trinomial. This is one of the ways to factor trinomials.
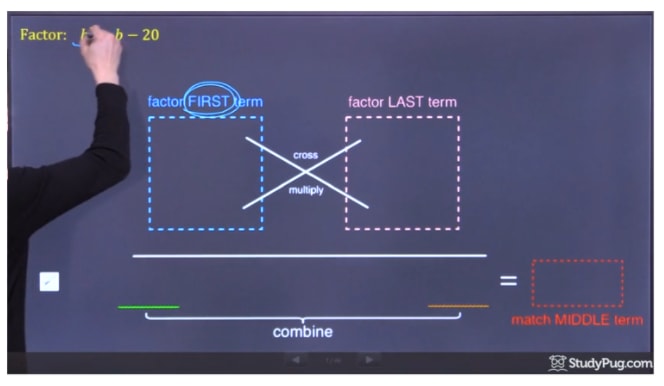
Factor the first term b2, put the results (b and b) in the first box.

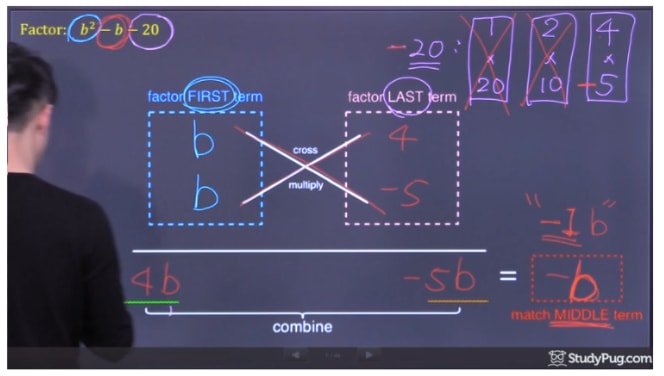
Factor the last term -20. There are a few combinations (1x20, 2x10, 4x5) that can give us 20, so which one is it? We'll cross-multiply those combinations to the factors of the first term. See which combination will produce an answer that matches the middle term (in this question, the middle term is –b).
Out of those combinations, 4x-5 (which equals -1) is able to produce the matching middle term -b.
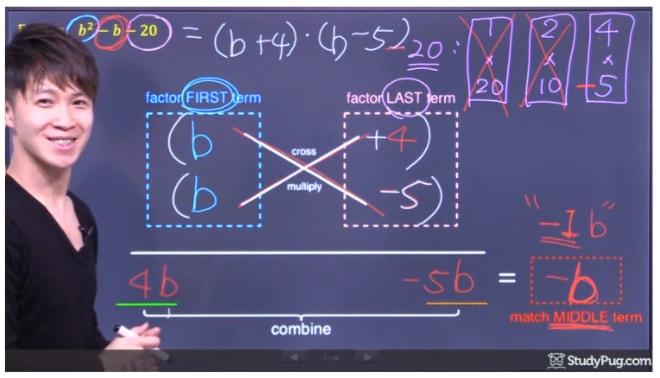
After all the steps, we successfully factored the trinomial b2−b−20 into (b+4)∙(b−5)
Question 2:
Factor: 2x2+25x+12
Solution:
The "cross-multiply, then check" method can also be used on harder trinomials in which the leading coefficient is not 1. In this question, the leading coefficient is 2 (from the leading term 2x2).
Now, we factor the first term 2x2. The result is 2x and x. we put them in the first box
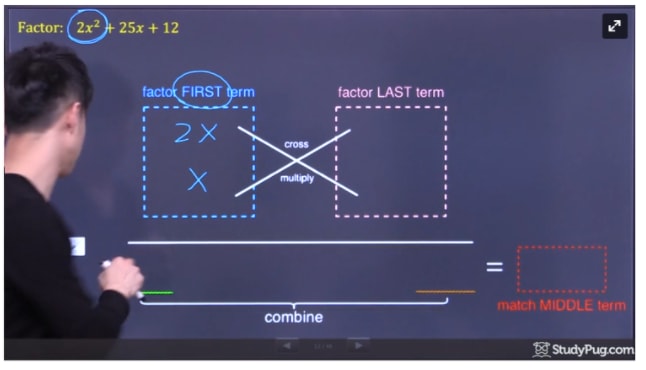
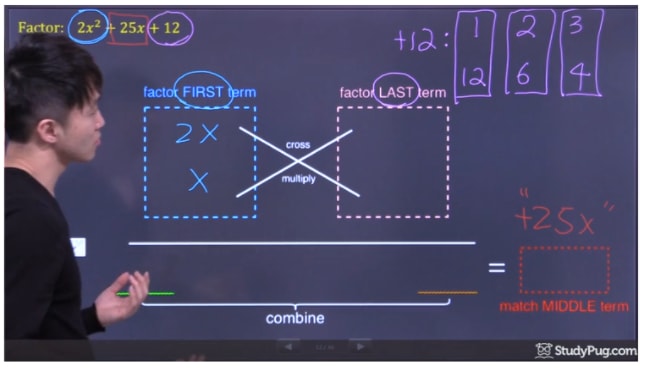
In order to factor the last term +12, there are a few combinations (1x12, 2x6, 3x4). We'll once again cross-multiply those combinations to the factors of the first term. See which combination will produce a matching middle term (in this question, the middle term is +25x)
Out of those combinations, 1x12 is able to produce the matching middle term +25x. That is because (2x x 12) + (x x 1) = 24x + x = 25x
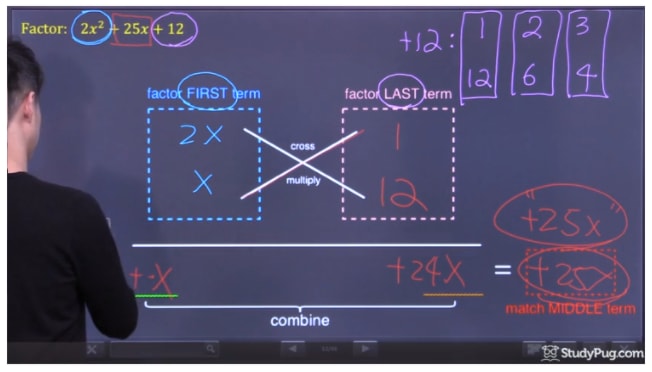
After all the steps, we successfully factored the trinomial 2x2+25x+12 into (2x+1)∙(x+12)

Factoring perfect square trinomials
As you do more questions that require you to do trinomial factoring, you may run into perfect square trinomials. These are trinomials that has both the "a" and "c" terms being perfect squares and the middle "b" being twice the product of the first and last term. Therefore, after factoring, you'll get an answer in the form of either (a+b)^2 or (a-b)^2.
There are good examples for you to further practice factoring trinomials. We've found some excellent online practice questions for you to try that keeps the answers hidden until you hover over the word "answer". There is also an online trinomial calculator for when you have a quadratic equation. It can help you factor any trinomial instantly! Use it to help you check your work.
Basic Concepts
remaining today
remaining today



