Combination of both parallel and perpendicular line equations
All in One PlaceEverything you need for better grades in university, high school and elementary. | Learn with EaseMade in Canada with help for all provincial curriculums, so you can study in confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Examples
Lessons
- Find the slope of a line that is parallel and perpendicular to the following.
- Given the equations of the following line determine if they parallel, perpendicular, or neither.
- Find the equation of the line that passes through given point and is i.) parallel ii.) perpendicular to the given line.
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
What are perpendicular lines
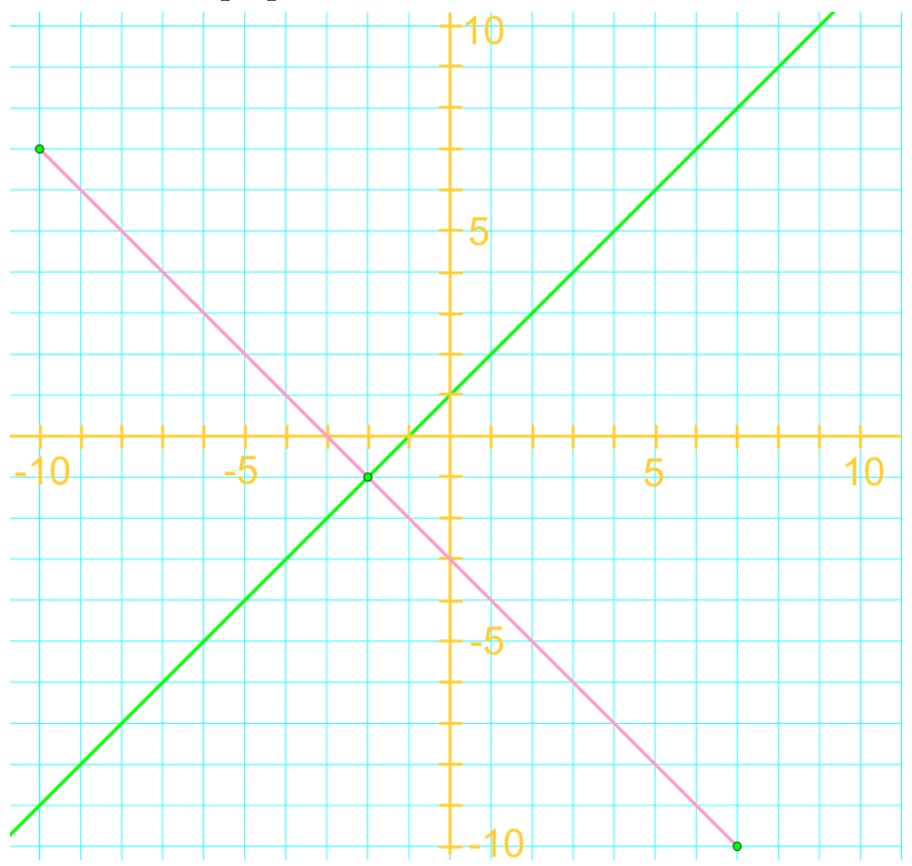
Perpendicular lines are two lines that meet and form a right angle at its intersection. In more advanced terms, when we multiply the slopes of perpendicular lines together, it gives us -1. Lines that are perpendicular are actually the negative reciprocals of each other. Later on, we'll explain further into what this actually means.
What are parallel lines?
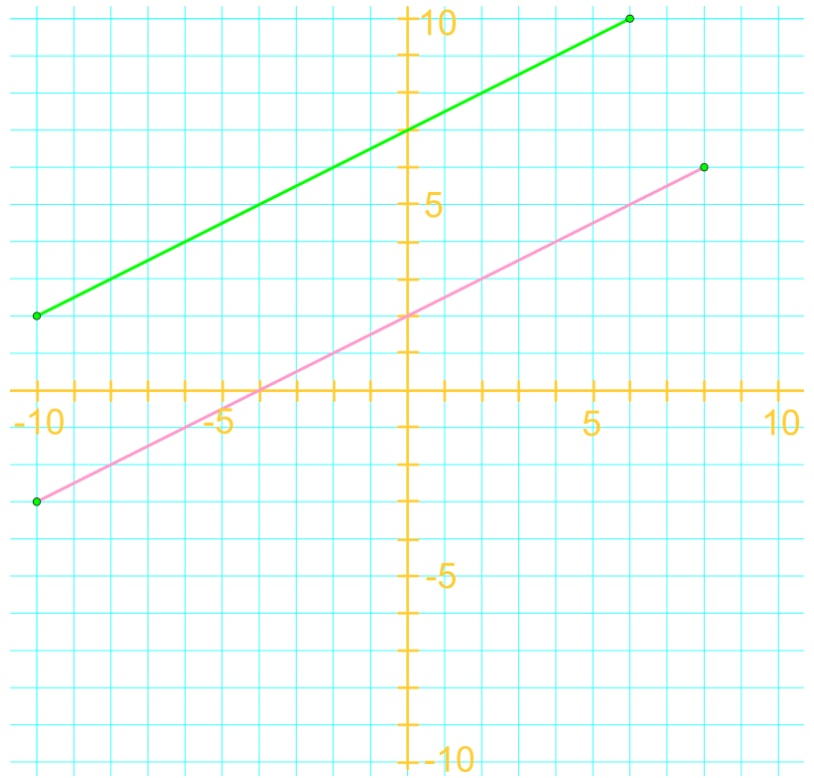
Parallel lines are lines that are the same distance apart and at no point touches one another. In other words, these two lines have the same slope. To be parallel, two lines must also be drawn or graphed on the same plane.
How to find a perpendicular line
To really understand how to determine perpendicular lines, let's use an example question. We're starting with simpler questions that ask you to determine just the slope of a line perpendicular or parallel to the line given, but you will need to find the perpendicular line equation or the parallel line equation of a line as you get to more advanced questions. We'll later use the same question to demonstrate how to find a parallel line as well.
Question:
Find the slope of a line that is perpendicular to the following:
y = (-2/3)x - 5
Solution
Slope of the equation= -2/3
Perpendicular slope: 3/2
We know that the question y=(-?)x - 5 is actually an equation in the slope-intercept form y = mx + b. Therefore, the slope m is equalled to -? in this case.
To find a perpendicular slope, flip the top and bottom of the original slope as this will give you the reciprocal (This is basically calculating 1/slope of original line, which means you'll essentially be flipping the top and bottom numbers). The perpendicular will just be equalled to -3/2 and then multiply it by -1. By multiplying it by -1, it gets rid of the negative and leaves you with 3/2.
The slope of a perpendicular line to y = (-2/3)x - 5 is 3/2.
How to find parallel lines
Recall back at the beginning of our explanation that parallel lines have the same slope. Let's take a look at the same line equation as the previous example, but this time, let's focus on the parallel line's slope.
Question:
Find the slope of a line that is parallel to the following:
y = (-2/3)x - 5
Solution:
Slope of the equation = -2/3
Slope of the parallel line = -2/3
Again, since the equation is in the slope-intercept form, we can easily tell that the slope is equalled to -?. Since the slope of a line parallel to this line has to have the same slope, the answer to this question to finding the parallel slope is simply -?.
Therefore, the slope of a parallel line to y = (-2/3)x -5 is -2/3.
Remember that when you are asked to find whether two lines are perpendicular or parallel that you take the time to find their slopes. Although you may know how to graph out the lines, you cannot accurately judge whether the lines are parallel or perpendicular with just your eye's estimate. For example, the slope could actually be very close to one another leading you to think they're identical and parallel, but in actual fact is a little different. Instead, finding out whether the lines' slopes are the same (that is, parallel) or when multiplied equals -1 (that is, perpendicular) is the best gauge.
You can explore the relationship between two lines that are parallel or perpendicular here.
Basic Concepts
remaining today
remaining today



