Taylor series and Maclaurin series
All in One PlaceEverything you need for better grades in university, high school and elementary. | Learn with EaseMade in Canada with help for all provincial curriculums, so you can study in confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Examples
Lessons
- Maclaurin Series
Find the Taylor or Maclaurin Series of the following functions without using the formulas: - Using the Formula to Find the Maclaurin Series
Use the formulas to find the Maclaurin Series for the following functions: - Finding the Taylor Series for Sine and Cosine
Show that sin(x)= ∑n=0∞(2n+1)!(−1)nx2n+1 - Finding the Taylor Series for Sine and Cosine
Show that cos(x)= ∑n=0∞(2n)!(−1)nx2n
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Taylor Series and Maclaurin Series
In order to understand Taylor and Maclaurin Series, we need to first look at power series.
What are Power Series?
A power series is basically a series with the variable x in it. Formally speaking, the power series formula is:
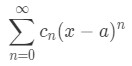
where cn are the coefficients of each term in the series and a is a constant. Power series are important because we can use them to represent a function. For example, the power series representation of the function f(x)=(1−x)1(for∣x∣ < 1) is:
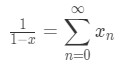
where a=1 and cn=1.However, what if I want to find a power series representation for the integral of (1−x)1? All you have to do is integrate the power series.
Find a Power Series Representation for the function
Question 1: Find a power series representation for the integral of the function
-
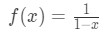
Equation 1: Power Series Representation integral pt.1 Recall that earlier we said that:
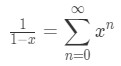
Equation 1: Power Series Representation integral pt.2 So if we integrate both sides, then we get:

Equation 1: Power Series Representation integral pt.3 To find c, we set x=0. So we have:
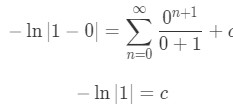
Equation 1: Power Series Representation integral pt.4 Notice that ln(1) is equal to 0. So we get:
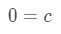
Equation 1: Power Series Representation integral pt.5 Hence we can conclude that:
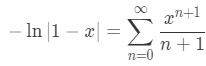
Equation 1: Power Series Representation integral pt.6 If you want, you can make the series start at n=1 instead, making the series become:
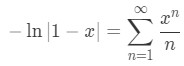
Equation 1: Power Series Representation integral pt.7
Power Series to a Taylor Series
Now this is where Taylor and Maclaurin Series come in. Taylor Series and Maclaurin Series are very important when we want to express a function as a power series. For example, ex and cosx can be expressed as a power series! First, we will examine what Taylor Series are, and then use the Taylor Series Expansion to find the first few terms of the series. Then we will learn how to represent some function as a Taylor series, and even differentiate or integrate them. Lastly, we will look at how to derive Taylor Polynomials from Taylor Series, and then use them to approximate functions. Note that we will also look at Maclaurin Series.
What is a Taylor Series
So what exactly are Taylor Series? If possible (not always), we can represent a function f(x) about x=a as a Power Series in the form:
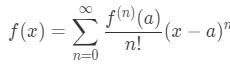
where fn(a) is the nth derivative about x=a. This is the Taylor Series formula. If it is centred around x=0, then we call it the Maclaurin Series. Maclaurin Series are in the form:
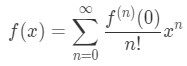
Here are some commonly used functions that can be represented as a Maclaurin Series:

We will learn how to use the Taylor Series formula later to get the common series, but first let's talk about Taylor Series Expansion.
Taylor Series Expansion
Of course if we expand the Taylor series out, we will get:
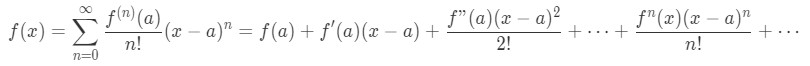
This is known as the Taylor Expansion Formula. We can use this to compute an infinite number of terms for the Taylor Series.
Finding the First Few Terms
For example, let's say I want to compute the first three terms of the Taylor Series ex about x=1.
Question 2: Find the first three terms of the Taylor Series for f(x)=ex.
- We will use the Taylor Series Expansion up to the third term. In other words, the first three terms are:
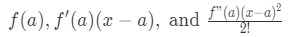
Equation 2: Taylor Expansion terms of e^x pt.1 Note that this is centred about x=1, hence we know
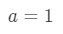
Equation 2: Taylor Expansion terms of e^x pt.2 We also know that taking derivatives gives us:
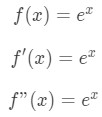
Equation 2: Taylor Expansion terms of e^x pt.3 Hence plugging a into each of these functions will give us:
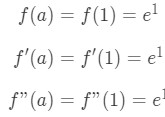
Equation 2: Taylor Expansion terms of e^x pt.4 So we know that the first three terms are:
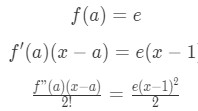
Equation 2: Taylor Expansion terms of e^x pt.5
Finding the Taylor Series
Instead of finding the first three terms of the Taylor series, what if I want to find all the terms? In other words, can I find the Taylor Series which can give me all the terms? This is possible; however it can be difficult because you need to notice the pattern. Let's try it out!
Question 3: Find the Taylor Series of f(x)=ex at x=1.
- Recall that the Taylor Expansion is:
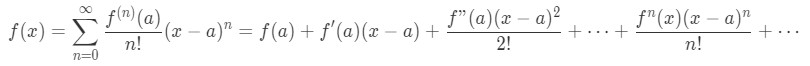
Equation 3: Taylor Series of e^x pt.1 We know the first three terms, but we don't know any terms after. In fact, there are an infinite amount of terms after the third term. So how is it possible to figure what the term is when n→∞? Well, we look for the pattern of the derivatives. If we are able to spot the patterns, then we will be able to figure out the nth derivative is. Let's take a few derivatives first. Notice that:
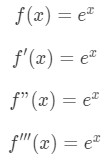
Equation 3: Taylor Series of e^x pt.2 The more derivatives you take, the most you realize that you will just get ex back. Hence we can conclude that the nth derivative is:

Equation 3: Taylor Series of e^x pt.3 Furthermore we know at a=1, hence
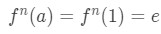
Equation 3: Taylor Series of e^x pt.4 Therefore plugging this in into the Taylor Series Formula gives:
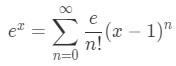
Equation 3: Taylor Series of e^x pt.5 Notice that this Taylor Series for ex is different from the Maclaurin Series for ex. This is because this one is centred at x=1, while the other is centred around x=0.You may have noticed that finding the nth derivative was really easy here. What if the nth derivative was not so easy to spot?
Question 4: Find the Taylor Series of f(x)=sinx centred around a=0.
- Notice that if we take a few derivatives, we get:

Equation 4: Taylor Series of sinx pt.1 Now the nth derivative is not easy to spot here because the derivatives keep switching from cosine to sine. However, we do notice that the 4th derivative goes back sinx again. This means that if we derive more after the 4th derivative, then we are going to get the same things again. We may see the pattern, but it doesn't tell us much about the nth derivative. Why don't we plug a=0 into the derivatives?
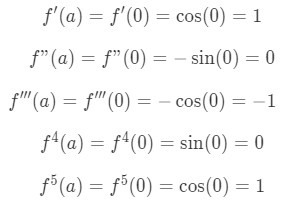
Equation 4: Taylor Series of sinx pt.2 Now we are getting something here. The values of the nth derivative are always going to be 0, -1, or 1. Let's go ahead and find the first six terms of the Taylor Series using these derivative.

Equation 4: Taylor Series of sinx pt.3 If we are to add all the terms together (including term after the sixth term), we will get:
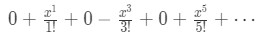
Equation 4: Taylor Series of sinx pt.4 This is the Taylor Expansion of sinx. Notice that every odd term is 0. In addition, every second term has interchanging signs. So we are going to rewrite this equation to:

Equation 4: Taylor Series of sinx pt.5 Even though we have these three terms, we can pretty much see the patterns of where this series is going. The powers of x are always going to be odd. So we can generalize the powers to be 2n+1. The factorials are also always odd. So we can generalize the factorials to be 2n+1. The powers of -1 always go up by 1, so we can generalize that to be n. Hence, we can write the Taylor Series sinx as
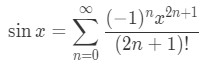
Equation 4: Taylor Series of sinx pt.6 which is a very common Taylor series. Note that you can use the same strategy when trying to find the Taylor Series for y=cosx.
Question 5: Find the Taylor Series of f(x) = cosx centred around.
- Notice that if we take a few derivatives, we get:

Equation 5: Taylor Series of cosx pt.1 Again, the nth derivative is not easy to spot here because the derivatives keep switching from cosine to sine. However, we do notice that the 4th derivative goes back cosx again. This means if we derive more after the 4th derivative, then we are going to get a loop. Now plugging in a=0 we have
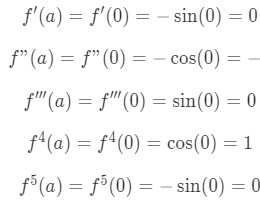
Equation 5: Taylor Series of cosx pt.2 Again, the values of the nth derivative are always going to be 0, -1, or 1. Let's find the first six terms of the Taylor Series using the derivatives from above.

Equation 5: Taylor Series of cosx pt.3 If we are to add all the terms together (including term after the sixth term), we will get:
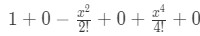
Equation 5: Taylor Series of cosx pt.4 Notice that this time all even terms are 0 and every odd term have interchanging signs. So we are going to rewrite this equation to:
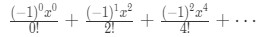
Equation 5: Taylor Series of cosx pt.5 We pretty much know the pattern here. The powers of x are always even. So we can generalize the powers to be 2n. The factorials are always even, so we can generalize them to be 2n. Lastly, the powers of -1 goes up by 1. So we can generalize that to be n. Hence, we can write the Taylor Series cosx as:
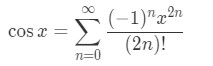
Equation 5: Taylor Series of cosx pt.6
Taylor Expansion Relationship of cosx and sinx
- Notice that the Maclaurin Series of cosx and sinx are very similar. In fact, they only defer by the powers. If we were to expand the Taylor series of cosx and sinx, we see that:
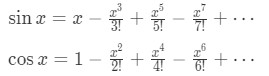
Equation 6: Taylor Expansion Relationship cosx and sinx pt.1 We can actually find a relationship between these two Taylor expansions by integrating. Notice that we were to find the integral of cosx, then
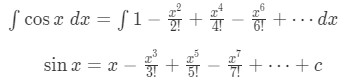
Equation 6: Taylor Expansion Relationship cosx and sinx pt.2 See that if x=0, then

Equation 6: Taylor Expansion Relationship cosx and sinx pt.3 So the integral of cosine is
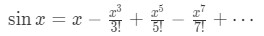
Equation 6: Taylor Expansion Relationship cosx and sinx pt.4 which is the Taylor Expansion of sinx. Likewise, the integral of sinx gives:
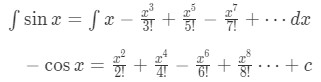
Equation 6: Taylor Expansion Relationship cosx and sinx pt.5 See if x=0, then,

Equation 6: Taylor Expansion Relationship cosx and sinx pt.6 Then we are left with:
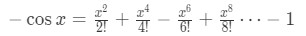
Equation 6: Taylor Expansion Relationship cosx and sinx pt.7 Dividing both sides of the equation by -1 gives:

Equation 6: Taylor Expansion Relationship cosx and sinx pt.8 which is the Taylor Expansion of cosx.
Taylor Series of Harder Functions
Now that we know how to use the Taylor Series Formula, let's learn how to manipulate the formula to find Taylor Series of harder functions.
Question 6:Find the Taylor Series of f(x)=xsinx.
- So we see that the function has sinx in it. We know that sinx has the common Taylor series:
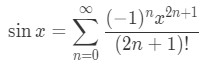
Equation 7: Taylor Series of sinx/x pt.1 So if we were to divide both sides by x, then we will get:
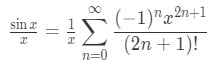
Equation 7: Taylor Series of sinx/x pt.2 We can manipulate the right hand side so that:
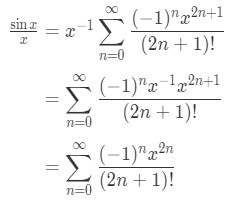
Equation 7: Taylor Series of sinx/x pt.3 and so we just found the Taylor series for xsinx. Let's do a harder question.
Question 7: Find the Taylor Series of
-
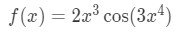
Equation 8: Taylor Series of 2x^3cos(3x^4) pt.1 Notice that cosine is in the function. So we probably want to use the Taylor Series:
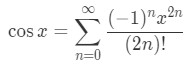
Equation 8: Taylor Series of 2x^3cos(3x^4) pt.2 See that inside the cosine is 3x4. So what were going to do is replace all the x's, and make them into 3x4. In other words,
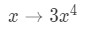
Equation 8: Taylor Series of 2x^3cos(3x^4) pt.3 Doing so gives us:

Equation 8: Taylor Series of 2x^3cos(3x^4) pt.4 Now we are going to multiply both sides of the equation by 2x3. This leads to:
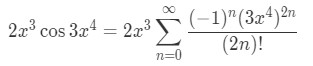
Equation 8: Taylor Series of 2x^3cos(3x^4) pt.5 Now we are going to clean up the series a little bit so that everything is inside the general term.
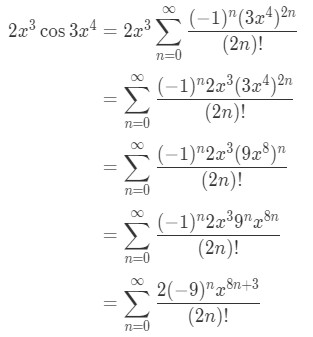
Equation 8: Taylor Series of 2x^3cos(3x^4) pt.6
Thus we are done and this is the Taylor Series of 2x3cos(3x4). If you want to do more practice problems, then I suggest you look at this link.
http://tutorial.math.lamar.edu/Problems/CalcII/TaylorSeries.aspxEach question has a step-by-step solution, so you can check your work!
Taylor Series Approximation
Note that the Taylor Series Expansion goes on as n→∞, but in practicality we cannot go to infinity. As humans (or even computers) we cannot go on forever, so we have to stop somewhere. This means we need to alter the formula for us so that it is computable.
We alter the formula will be:
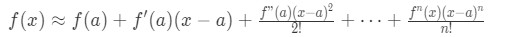
Notice that since we stopped looking for terms after n, we have to make it an approximation instead. This formula is known as the Taylor approximation. It is a well known formula that is used to approximate certain values.
Notice on the right hand side of the equation that it is a polynomial of degree n. We actually call this the Taylor polynomial Tn(x). In other words, the Taylor polynomial formula is:
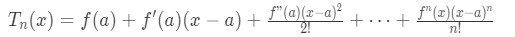
Let's do an example of finding the Taylor polynomial, and approximating a value.
Question 8: Find the 3rd degree Taylor Polynomial of f(x)=ln(x) centred at a=1. Then approximate ln(2).
- If we are doing a Taylor Polynomial of degree 3 centred at a=1, then use the formula up to the 4th term:
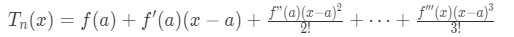
Equation 9: Taylor Series Polynomial lnx pt.1 Notice that taking the derivatives gives us:
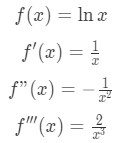
Equation 9: Taylor Series Polynomial lnx pt.2 We also know that a=1, so:
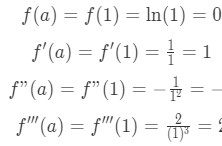
Equation 9: Taylor Series Polynomial lnx pt.3 Just in case you forgot, ln1 gives us 0. That's why f(a)=0. Now plugging everything into the formula of the 3rd degree Taylor polynomial gives:
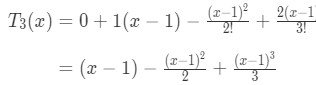
Equation 9: Taylor Series Polynomial lnx pt.4 Now we have to approximate ln(2). In order to do this, we need to use the Taylor polynomial that we just found. Notice that according to the Taylor approximation:
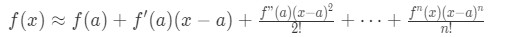
Equation 9: Taylor Series Polynomial lnx pt.5 This means that:
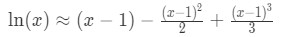
Equation 9: Taylor Series Polynomial lnx pt.6 If we are to set x=2, then we will see that:

Equation 9: Taylor Series Polynomial lnx pt.7 So ln(2) is approximately around 65. See that 65 in decimal form is 0.833333...
Now if you pull out your calculator, we are actually pretty close. The actual value of ln(2) is 0.69314718056....
The Error Term
We know that Taylor Approximation is just an approximation. However, what if we want to know the difference between the actual value and the approximated value? We call the difference the error term, and it can be calculated using the following formula:
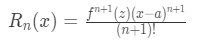
Keep in mind that the z variable is a value that is between a and x, which gives the largest possible error.
Let's use the error term formula to find the error of our previous question.
Question 9: Find the error of ln(2).
- In order to find the error, we need to find
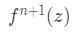
Equation 10: Taylor Series Error term ln(2) pt.1 Notice from our previous question that we found the Taylor polynomial of degree 3. So we set n=3. This means we need to find:
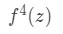
Equation 10: Taylor Series Error term ln(2) pt.2 See that the fourth derivative of the function is:
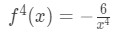
Equation 10: Taylor Series Error term ln(2) pt.3 Now our function is in terms of x, but we need it in term of z. So we just set z=x. This means that:

Equation 10: Taylor Series Error term ln(2) pt.4 So plugging this into our error term formula gives us:
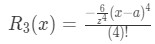
Equation 10: Taylor Series Error term ln(2) pt.5 Remember that we set x=2 and a=1, so we have:
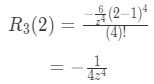
Equation 10: Taylor Series Error term ln(2) pt.6 Since we are talking the error of our approximation, the negative sign doesn't matter here. So realistically we are looking at:
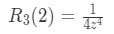
Equation 10: Taylor Series Error term ln(2) pt.7 Now recall that z is a number between a and x which makes the error term the largest value. In other words, z must be:
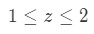
Equation 10: Taylor Series Error term ln(2) pt.8 because a=1, and x=2. Now what z value must we pick so that our error term is the largest?
Notice that the variable z is in the denominator. So if we pick smaller values of z, then the error term will become bigger. Since the smallest value of z we can pick is 1, then we set z=1. Thus,
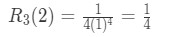
Equation 10: Taylor Series Error term ln(2) pt.9 is our error.
Taylor's Theorem
Now think of it like this. If we were to add the error term and the approximated value together, wouldn't I get the actual value? This is correct! In fact, we can say this formally. If the Taylor polynomial is the approximated function and Rn(x) is the error term, then adding them gives the actual function. In other words,
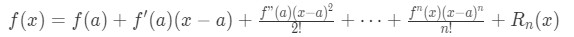
This is known as Taylor Theorem.
∑n=0∞n!f(n)(a)(x−a)n
where f(n)(a) is the n'th derivative at x=a. If a=0, then we call it a Maclaurin Series. A Maclaurin Series is in the form:
∑n=0∞n!f(n)(a)xn
Here are some formulas that may be of use:
ex=∑n=0∞n!xn
sin(x)=∑n=0∞(2n+1)!(−1)nx2n+1
cos(x)=∑n=0∞(2n)!(−1)nx2n
remaining today
remaining today



