Alternating series test
All in One PlaceEverything you need for better grades in university, high school and elementary. | Learn with EaseMade in Canada with help for all provincial curriculums, so you can study in confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Alternating Series Test
The alternating series test (also known as the Leibniz test), is type of series test used to determine the convergence of series that alternate. Keep in mind that the test does not tell whether the series diverges. In order to use this test, we first need to know what a converging series and a diverging series is.
What is a convergent series? What is a divergent series?
A convergent series is an infinite series which sums up to a finite number. For example, the famous convergent series:
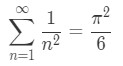
This convergent series sum up to 6π2! How do you get that? It is a long process that requires a lot of calculations, but usually it is sufficient enough to know that the series is convergent by the p-series test.
A divergent series is an infinite series where the sum is infinity. For example, the series
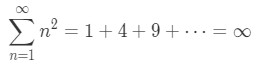
Adding up all the numbers will give you a sum of infinity. If that doesn't convince you, take a look at this. Note that the series could be written as an Nth partial sum.
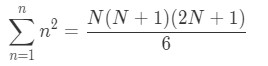
Now if we were to make it an infinite series, then we are going to take the limit as N goes to infinity of both sides. In other words,
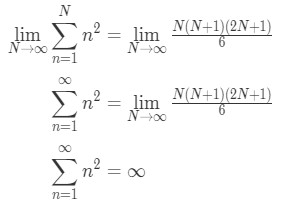
Now that we know what a divergent and convergent series is, let's take a look at the alternating series test.
Alternating Series Test
In order to use the alternating series test, the series must be alternating. In other words, the series are in the form:
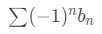
or
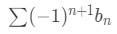
where bn≤0. An alternating series is not limited to these two forms because the exponent on the (-1) can vary. Now the alternating series test states that if the two following conditions are met, then the alternating series is convergent:

For the second condition, bn does not have to be strictly decreasing for all n≤1. As long as the sequence is decreasing at n→∞, then that will be sufficient enough to show that it is decreasing. Now that we know what the alternating series test is, let us put it to use for the following examples.
Example 1: Show that the series
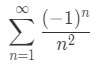
is convergent.
Before we want to use the alternating series test, we want to make sure that the series is actually alternating. In other words, turn this series into the form:
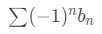
As you can see, we can turn our series into that form. Notice that:
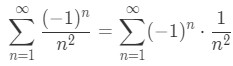
And so we know that:
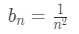
Hence, we can go ahead and use the alternating series test. Now remember the two conditions. First we have to show that
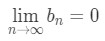
Since our bn=n21, then our limit is

Notice that this limit does to 0, hence
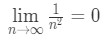
and so our first condition is fulfilled. Now let's take a look at the second condition. We have to make sure that n21 is decreasing. How do we do this? There are a total of three ways to do this:
-
Method 1:
Write out the first few terms We can write out the first few terms of bn and then conclude if the sequence is decreasing. Notice that:Notice how the numerator never changes, but the denominator is getting bigger and bigger. As the denominator gets bigger, then the numbers itself get smaller. Hence we can conclude that the sequence is decreasing, and condition is fulfilled. Some teachers may not see this method as legitimate for more complicating questions (because it's harder to compare). In that case, look at the other methods.
Equation 2: Alternating Series test pt.8 -
Method 2:
Compare the nth term and (n+1)th term of the sequence bn.
Notice that the nth term of the sequence bn is:
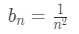
Equation 2: Alternating Series test pt.9 And the (n+1)th term is
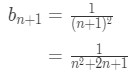
Equation 2: Alternating Series test pt.10 Now comparing the two terms, you should notice that:
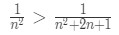
Equation 2: Alternating Series test pt.11 The left side is bigger than the right side because the denominator in the right side is bigger, hence the term is actually smaller. So we just concluded that:
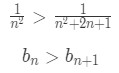
Equation 2: Alternating Series test pt.12 for all n>1. This means that the nth term is always going to be bigger than the (n+1)th term, which means the sequence is always decreasing. Hence again, the second condition is fulfilled. Again, sometimes it's really hard to compare the two terms. In this case, look at method 3.
-
Method 3:
Take the derivative
What were going to do is take the general term (bn) and change all the n's to x's, and set it as f(x). In other words,
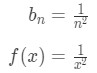
Equation 2: Alternating Series test pt.13 Now we are going to take the derivative of this function. This will give us:
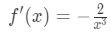
Equation 2: Alternating Series test pt.14 Notice that for x > 0, the denominator is going to be positive, and so the derivative f'(x) is negative. In other words, for increasing value of x, the function is decreasing. Now let's put that into the perspective of bn. This means that for increasing values of n, the sequence bn is always decreasing. Thus, we just fulfilled the second condition again.
Since the two conditions are fulfilled, then we can conclude that the series
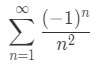
Equation 2: Alternating Series test pt.15 converges. Now let's take a look at a more interesting alternating series.
Example 2: Consider the alternating harmonic series:
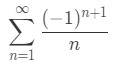
Is it convergent? If it is, then what is the sum of this series?
- What should we do here? You are probably thinking about one of the series convergence tests. You are most likely thinking about using the alternating series test. Again, we need to show that this is in fact an alternating series before we can apply the alternating series test. Recall that an alternating series could be of the form:
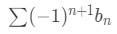
Equation 3: Harmonic Alternating Series pt.2 - Notice that:
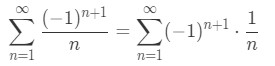
Equation 3: Harmonic Alternating Series pt.3 - And so we know that
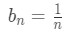
Equation 3: Harmonic Alternating Series pt.4 - Since we know that it is an alternating series, then we can see if the two conditions are fulfilled. For the first condition, we see that:
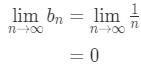
Equation 3: Harmonic Alternating Series pt.5 - So the first condition is fulfilled. Now the second condition states that bn must be a decreasing sequence. Feel free to use any of the methods, but I will be using method two. See that the nth term and (n+1)th term are
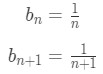
Equation 3: Harmonic Alternating Series pt.6 - Notice by comparing nth term and (n+1)th term of the sequence, we have:
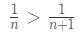
Equation 3: Harmonic Alternating Series pt.7 - Again, this is because the denominator on the right side is bigger, so the term is actually smaller. In other words, we just concluded that:
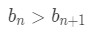
Equation 3: Harmonic Alternating Series pt.8 - For n>1. Hence, every term after is smaller than the one before it. So we can conclude that the sequence is decreasing. Since both of the conditions are fulfilled, then the series is convergent. But what is the sum of the series? Fortunately, there is an easy way to find this. First, we must recognize the Maclaurin series:
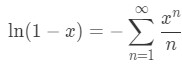
Equation 3: Harmonic Alternating Series pt.9 - Now if we were to set x = -1, then we will see that

Equation 3: Harmonic Alternating Series pt.10 - In other words, we just concluded that:
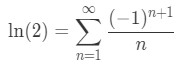
Equation 3: Harmonic Alternating Series pt.11
So the sum of this alternating harmonic series is ln(2). If you want to take a look at more examples of using the alternating series test, click on this link.
http://tutorial.math.lamar.edu/Classes/CalcII/AlternatingSeries.aspxNow here is an interesting question. If the alternating harmonic series is convergent, then what about the harmonic series itself? Is
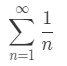
convergent or divergent? You may realize that this isn't an alternating series, so we are going to have to use another test. Why don't we use the nth term test?
nth term test for divergence
Recall that the nth term test (also known as the divergence test) states the following:
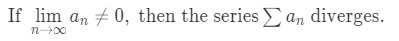
So if we take the limit and it is anything BUT 0, then we can say that the series diverge. However, if it does equal 0, then it does NOT mean the series converge. It just means the test has failed, and you would have to use something else to test the convergence.
Now using this test for the harmonic series we let:
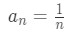
Then you will see that:

Since we've got 0, then the nth term test has failed and we would have to try something else. This leads to the question, maybe the harmonic series really converges?
Does 1/n converge
Let us assume that the harmonic series is convergent. Then that means the series must sum up to a finite number. Let's call that sum S. So
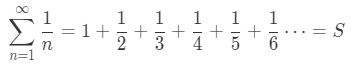
Now we are going to play a little trick here. We can say that:
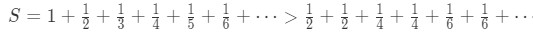
However on the right hand side of the inequality, see that

In other words, we are saying that
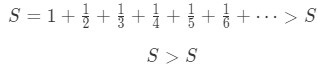
This is impossible, so we reached a contradiction. This situation causes us to get a mathematically illogical statement, so then the harmonic series must be divergent. A lot of people get confused by this method, so I have prepared another easier method to show that the harmonic series diverges. This method will require you to know the p-series rules.
Recall that p-series are in the form:
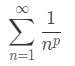
The p-series rule (or p-series test) states that if p>1, then the series converge. Otherwise, the series diverge. Notice that the series that we have is very similar to it.
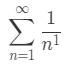
In fact, our p=1 in this case. We also know that p=1≯1, so then we know that the series diverge. Now we kind of went off topic here, but you must have realized that removing the (−1)(n+1) from the series can actually change the convergence or divergence of a series.
Alternating Series Estimation Theorem
So we learned that it is possible to find the sum of an alternating harmonic series using a complicated formula that we were unfamiliar with. But what if we are dealing with another alternating series? How would we find the sum? Unfortunately there is no good way to find the exact sum of converging alternating series, but there is a way to estimate the sum. It is called the alternating series estimation theorem.
The alternating series estimation theorem states the following:
Suppose that the alternating series
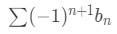
Is convergent and converges to a finite number S. Then
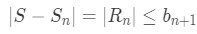
where:
Sn = the partial sum of n terms (sum of the first n terms)
Rn = the remainder (or error term) that we get from subtracting the actual value of the series with the sum of the first n terms. Sometimes it's called the alternating series error.
bn+1 = the neglected term.
Note that this theorem only works if the series is alternating. You are probably very confused at what this theorem is saying, so let us use a series as an example.
Example 3: Let's take a look at the alternating harmonic series we used earlier:
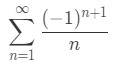
- Let's expand the series out. Doing so will give us:

Equation 5: Harmonic Alternating Series Estimation pt.2 - Now let's say that we want to estimate the sum of this series. What I'm going to do is estimate the sum of the series by summing the first 4 terms. Summing the first 4 terms gives us:

Equation 5: Harmonic Alternating Series Estimation pt.3 - Since we only look at the first 4 terms, then the next term after it (the 5th term) is the neglected term. Recall that the series can be rewritten as
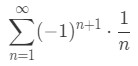
Equation 5: Harmonic Alternating Series Estimation pt.4 - So bn=n1, and hence
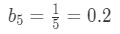
Equation 5: Harmonic Alternating Series Estimation pt.5 - Now what the theorem says is that
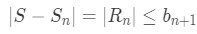
Equation 5: Harmonic Alternating Series Estimation pt.6 - So using the 2 pieces of information that we have, then
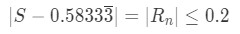
Equation 5: Harmonic Alternating Series Estimation pt.7 - Our remainder is kind of in the way of our equation, so we can get rid of it and have
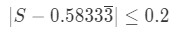
Equation 5: Harmonic Alternating Series Estimation pt.8 - Now instead of having the absolute value, we can rewrite our inequality to be:
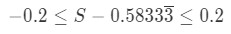
Equation 5: Harmonic Alternating Series Estimation pt.9 - Adding 0.58333 to all sides of the inequality gives us:
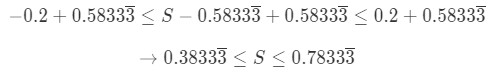
Equation 5: Harmonic Alternating Series Estimation pt.10 - Hence, we just estimate what the sum of the series is! It must be between 0.38333 and 0.78333. Note that you can also do this by summing the first 5 term or the first 11 terms. Usually the questions you will be dealing with will tell you how many terms you need to sum. In fact, as you sum more and more terms and use this theorem, your estimation becomes more and more accurate.
Now let's take a look at a question where we don't know how many terms we need to sum, but we know that our remainder (or error) has to be less than a certain number.
Example 4: Determine the number of terms required to approximate the sum of the series
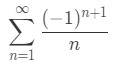
with an error of less than 0.0001.
- Recall that the theorem states that:
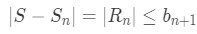
Equation 6: Harmonic Alternating Series Error pt.2 - If the error must be less than 0.0001, then basically we are saying that
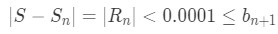
Equation 6: Harmonic Alternating Series Error pt.3 - or in a more simple manner,
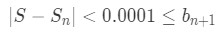
Equation 6: Harmonic Alternating Series Error pt.4 - Now we can't really do anything with this inequality because there are too many unknowns. So we need to think of a better way to do this. This is where it gets a little tricky because we actually have to think about this.
- Instead of saying that 0.0001 is less than the neglected term (0.0001≤bn+1), why don't we say that the neglected term is less than 0.0001. In other words, let's say that
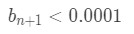
Equation 6: Harmonic Alternating Series Error pt.5 - Why? Think about it. We know that
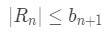
Equation 6: Harmonic Alternating Series Error pt.6 - The error term is less than the neglected term. So if the neglected term is less than 0.0001, then it must be true that the error term is less than 0.0001. Basically we are saying that:
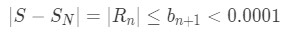
Equation 6: Harmonic Alternating Series Error pt.7 - So this works! Now going back to our inequality
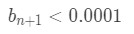
Equation 6: Harmonic Alternating Series Error pt.8 - We know that
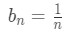
Equation 6: Harmonic Alternating Series Error pt.9 - So
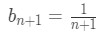
Equation 6: Harmonic Alternating Series Error pt.10 - That means
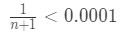
Equation 6: Harmonic Alternating Series Error pt.11 - We can rewrite this inequality to be:
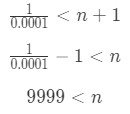
Equation 6: Harmonic Alternating Series Error pt.12 -
That means as long as n > 9999, then the error (or remainder) will be less than 0.0001. Let's pick n=10000. This means that summing the first 10000 terms will guarantee the error to be less than 0.0001. That is a lot of terms to sum up! If you want to look at more examples, then take a look at this link:
http://mathonline.wikidot.com/error-estimation-for-approximating-alternating-series
∑(−1)nbn
or
∑(−1)n+1bn
Where bn≥0 An alternating series is not limited to these two forms because the exponent on the (-1) can vary.
The Alternating Series Test states that if the two following conditions are met, then the alternating series is convergent:
1. limn →∞ bn=0
2. The sequence bn is a decreasing sequence.
For the second condition, bn does not have to be strictly decreasing for all n≥1. As long as the sequence is decreasing for n→∞, then that will be sufficient enough.
remaining today
remaining today



