Finding an exponential function given its graph
All in One PlaceEverything you need for better marks in university, secondary, and primary classes. | Learn with EaseWe’ve mastered courses for WA, NSW, QLD, SA, and VIC, so you can study with confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
What Are Exponential Functions?
Before we get into dealing with exponential functions and graphing exponential functions, let's first take a look at the general formula and theory behind exponential functions.
Below is one of the most general forms of an exponential graph:
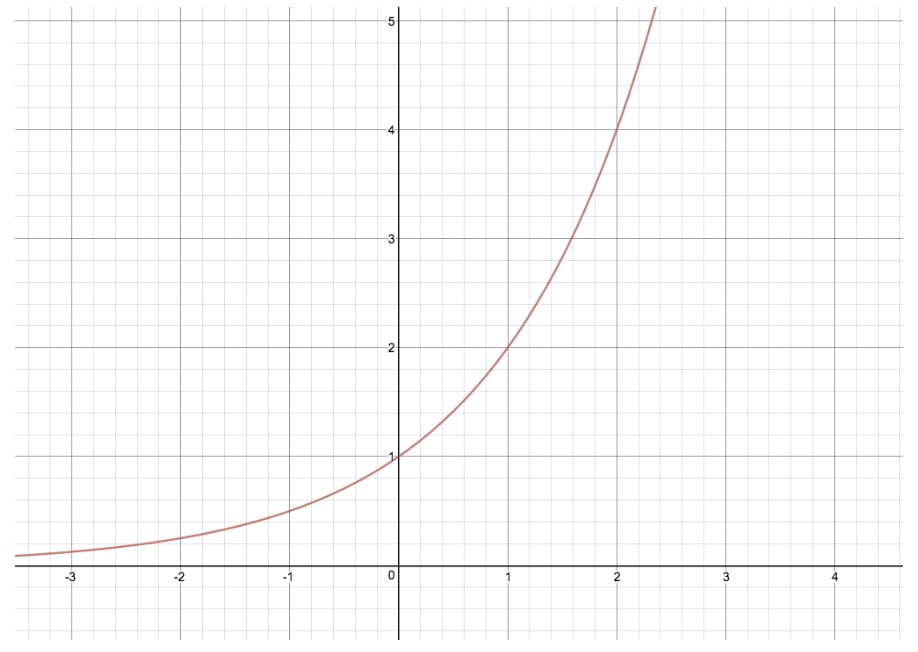
The exponential function equation to this graph is y=2x, and is the most simple exponential graph we can make. If you're wondering what y=1x would look like, here's its exponential graph:
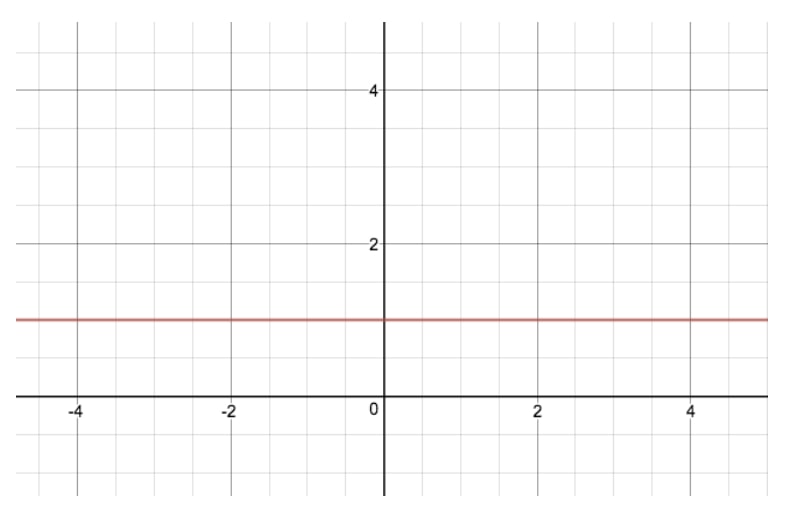
Now, as to the reason why the graphs of y=2x and y=1x are so different, the best way to understand the theory behind exponential functions is to take a look at some tables.

Above you can see three tables for three different "base values" – 1, 2 and 3 – all of which are to the power of x. As you can see, for exponential functions with a "base value" of 1, the value of y stays constant at 1, because 1 to the power of anything is just 1. That is why the above graph of y=1x is just a straight line. In the case of y=2x and y=3x (not pictured), on the other hand, we see an increasingly steepening curve for our graph. That is because as x increases, the value of y increases to a bigger and bigger value each time, or what we call "exponentially".
Now that we have an idea of what exponential equations look like in a graph, let's give the general formula for exponential functions:
y=abd(x−c)+k
The above formula is a little more complicated than previous functions you've likely worked with, so let's define all of the variables.
y – the value on the y-axis
a – the vertical stretch or compression factor
b – the base value
x – the value on the x-axis
c – the horizontal translation factor
d – the horizontal stretch or compression factor
k – the vertical translation factor
In this lesson, we'll only be going over very basic exponential functions, so you don't need to worry about some of the above variables. But, so you have access to all of the information you need about exponential functions and how to graph exponential functions, let's outline what changing each of these variables does to the graph of an exponential equation.
1) Variable "a"
Let's compare the graph of y=2x to another exponential equation where we modify "a", giving us y=(−4)2x

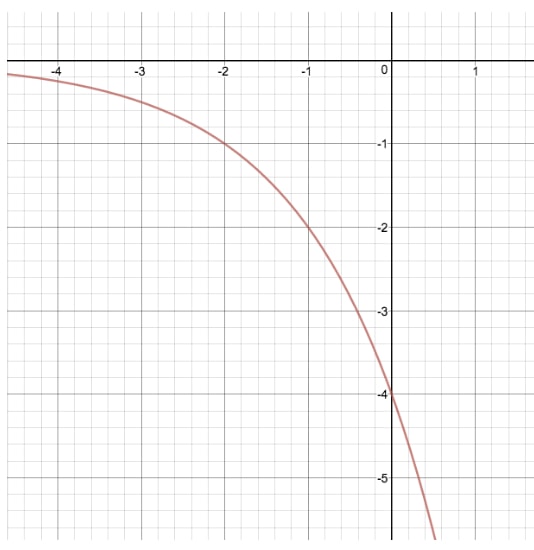
By making this transformation, we have both "stretched" and "reflected" the original graph of y=2x by it's y-values. In order to find "a" by looking at the graph, the most important thing to notice is that when x=0 and we don't have a value for "k", the y-intercept of our graph is always going to be equal to "a".
2) Variable "b"
Also known as the "base value" this is simply the number that has the exponent attached to it. Finding it involves algebra, which will be discussed later in this article.
Variable "c"
Let's compare the graph of y=2x to another exponential equation where we modify "c", giving us y=2(x−2)

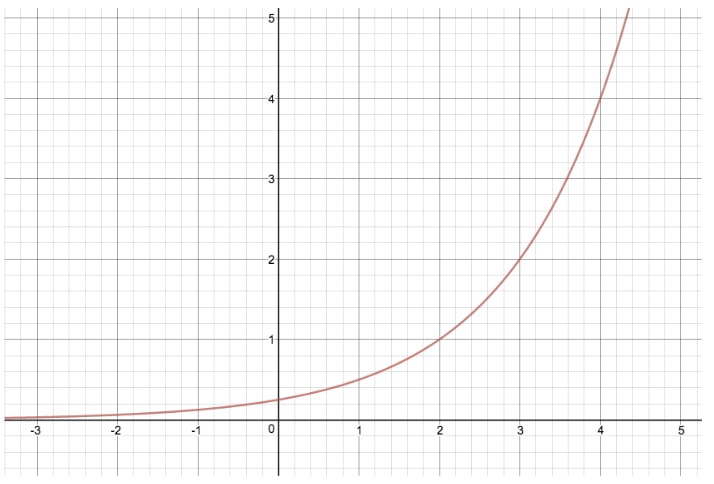
By making this transformation, we have shifted the entire graph to the right two units. If "c" was equal to -2, we would have shifted the entire graph to the left two units.
Variable "d"
Let's compare the graph of y=2x to another exponential equation where we modify "d", giving us y=24x

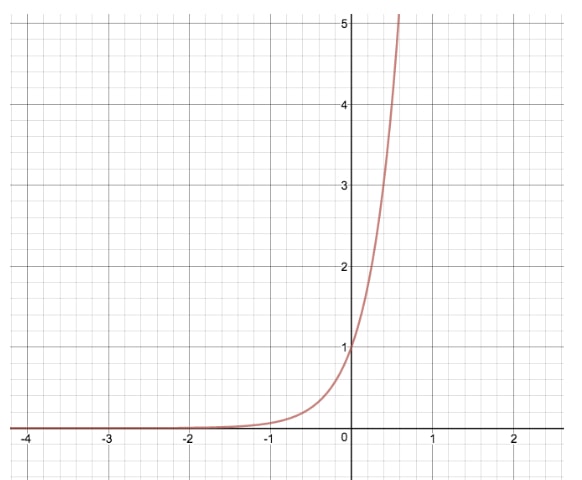
By making this transformation, we have stretched the original graph of y=2x by its x-values, similar to how the variable "a" modifies the function by its y-values. If "d" were negative in this example, the exponential function would undergo a horizontal reflection as opposed to the vertical reflection seen with "a".
Variable "k"
Let's compare the graph of y=2x to another exponential equation where we modify "k", giving us y=2x+2

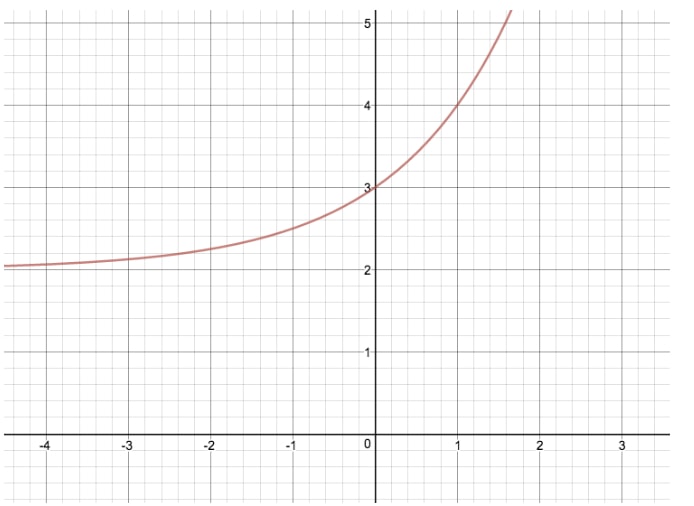
By making this transformation, we have translated the original graph of y=2x up two units. If "k" were negative in this example, the exponential function would have been translated down two units. "k" is a particularly important variable, as it is also equal to what we call the horizontal asymptote! An asymptote is a value for either x or y that a function approaches, but never actually equals.
Take for example the function y=2x: for this exponential function, k=0, and therefore the "horizontal asymptote" equals 0. This makes sense, because no matter what value we put in for x, we will never get y to equal 0. For our other function y=2x+2, k=2, and therefore the horizontal asymptote equals 2. There is no value for x we can use to make y=2.
And that's all of the variables! Again, several of these are more complicated than others, so it will take time to get used to working with them all and becoming comfortable finding them. To get a better look at exponential functions, and to become familiar with the above general equation, visit this excellent graphing calculator website here. Take your time to play around with the variables, and get a better feel for how changing each of the variables effects the nature of the function.
Now, let's get down to business. Given an exponential function graph, how can we find the exponential equation?
How To Find Exponential Functions
Finding the equation of exponential functions is often a multi-step process, and every problem is different based upon the information and type of graph we are given. Given the graph of exponential functions, we need to be able to take some information from the graph itself, and then solve for the stuff we are unable to take directly from the graph. Below is a list of all of the variables we may have to look for, and how to usually find them:
a – solve for it using algebra, or it will be given
b – solve for it using algebra, or it will be given
c – let x = 0 and imagine "c" is not there, the value of y will equal the y-intercept; now count how many units the y value for the y-intercept is from the y-axis, and this will equal "c"
d – solve for it using algebra
k – equal to the value of the horizontal asymptote
Of course, these are just the general steps you need to take in order to find the exponential function equation. The best way to learn how to do this is to try some practice problems!
Exponential Functions Examples:
Now let's try a couple examples in order to put all of the theory we've covered into practice. With practice, you'll be able to find exponential functions with ease!
Example 1:
Determine the exponential function in the form y=abx of the given graph.
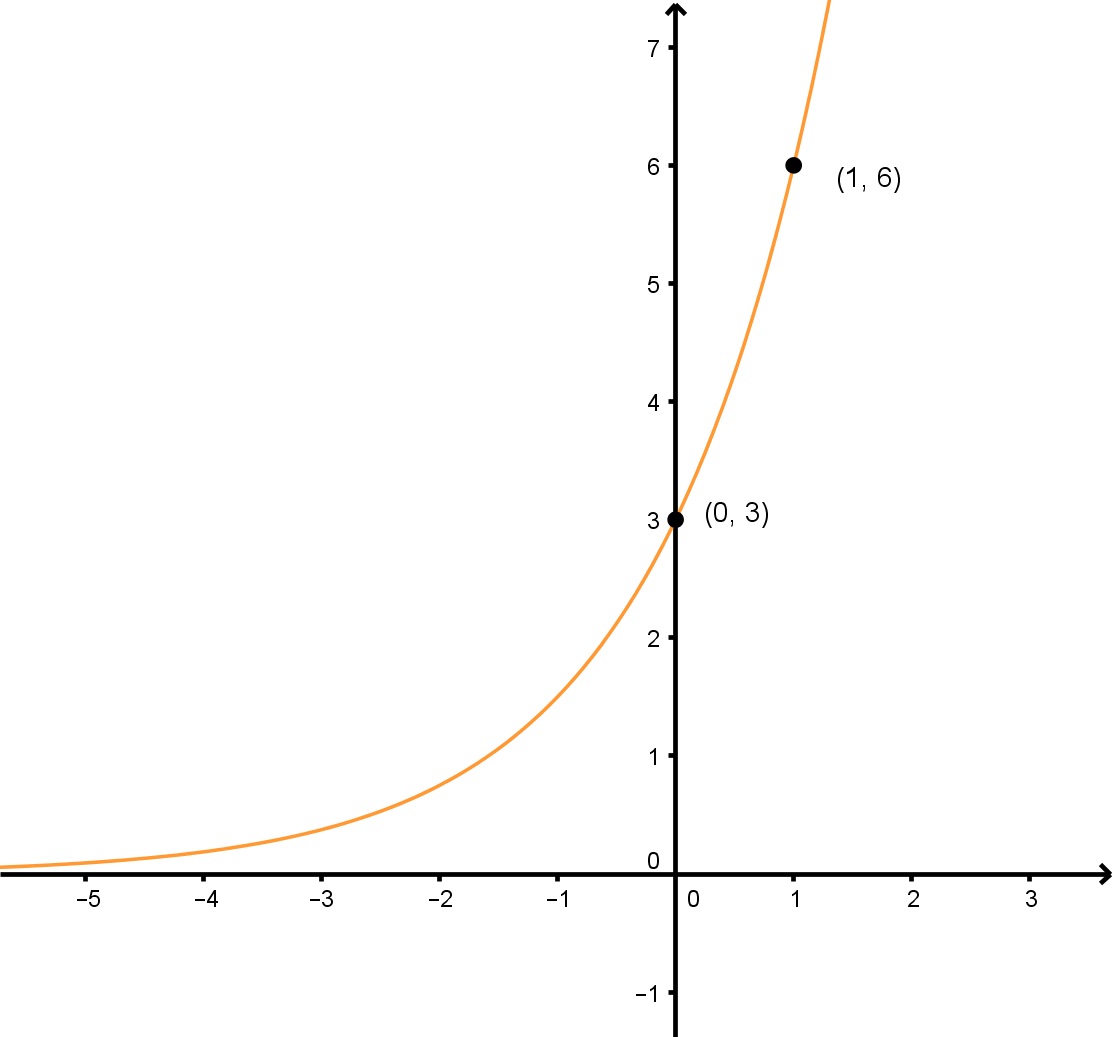
In order to solve this problem, we're going to need to find the variables "a" and "b". As well, we're going to have to solve both of these algebraically, as we can't determine them from the exponential function graph itself.
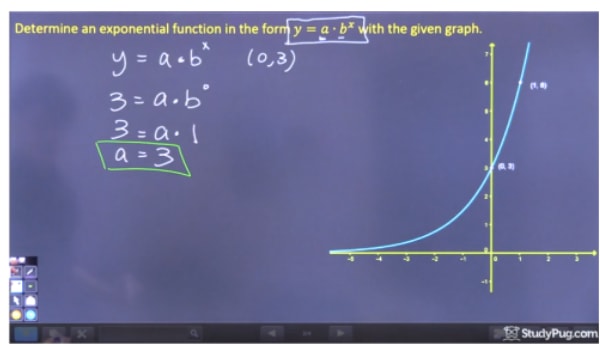
Step 1: Solve for "a"
To solve for "a", we must pick a point on the graph where we can eliminate bx because we don't yet know "b", and therefore we should pick the y-intercept (0,3). Since b0 equals 1, we can find that a=3. As a shortcut, since we don't' have a value for k, a is just equal to the y-intercept of this equation.
Step 2: Solve for "b"
Now that we have "a", all we have to do is sub in 3 for "a", pick another point, and solve for b. Let's pick the point (1,6). With all this information, we can find that b=2.
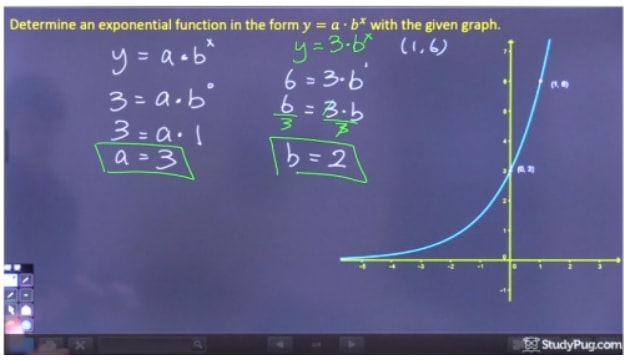
Step 3: Write the Final Equation
Now we that we have found all of the necessary variables, all that's left is to write out our final equation in the form y=abx. Our final answer is y=(3)2x
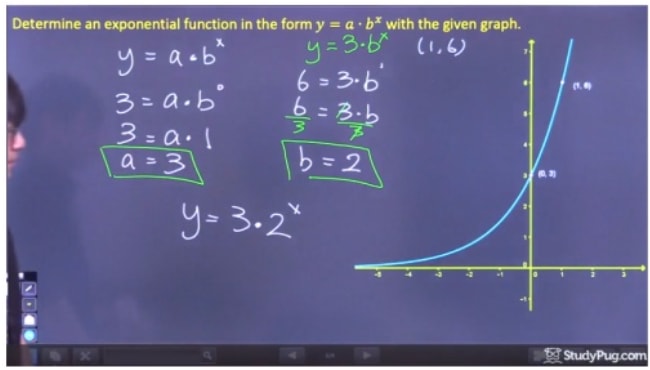
Example 2:
Determine the exponential function in the form y=a2dx+k of the given graph.
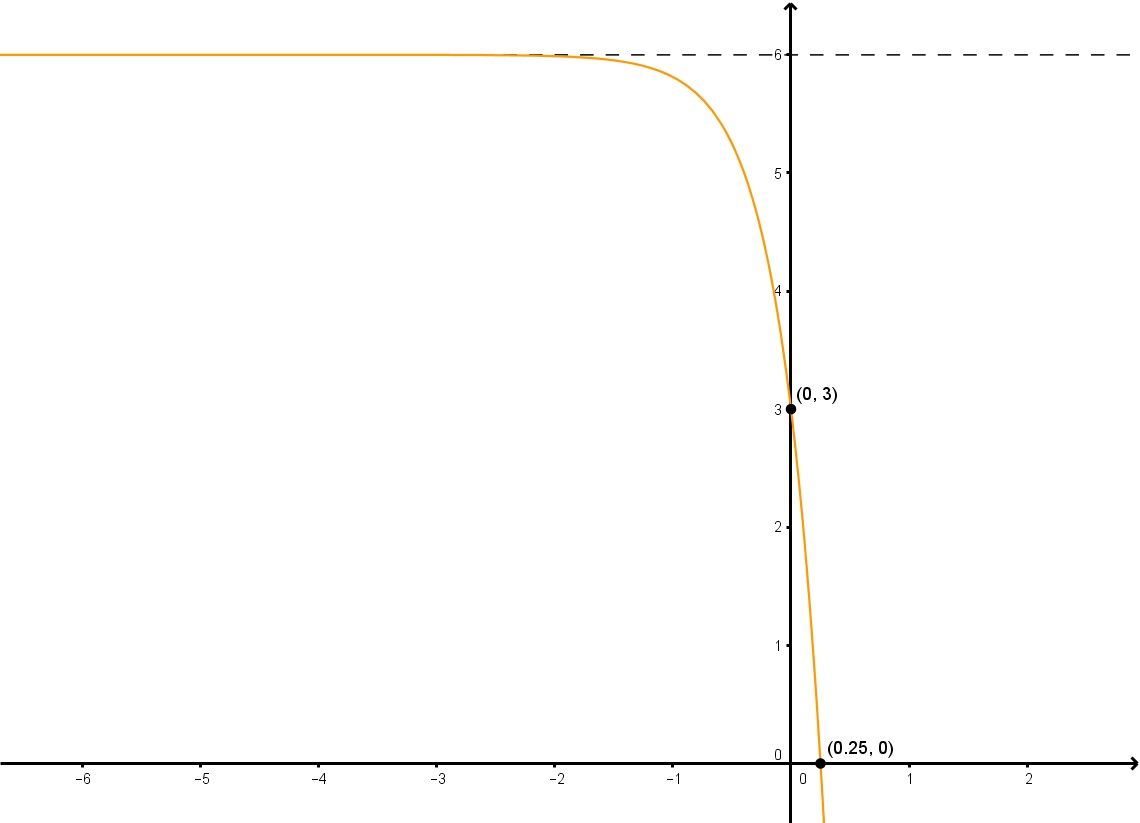
In order to solve this problem, we're going to need to find the variables "a", "d" and "k". Remember, we can find "k" from the graph, as it is the horizontal asymptote. For "a" and "d", however, we're going to have to solve for these algebraically, as we can't determine them from the exponential function graph itself.
Step 1: Find "k" from the Graph
To find "k", all we need to do is find the horizontal asymptote, which is clearly y=6. Therefore, k=6.
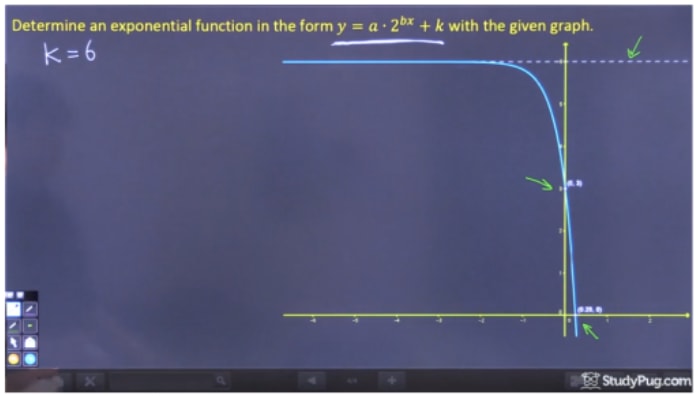
Step 2: Solve for "a"
To solve for "a", just like the last example, we must pick a point on the graph where we can eliminate 2dx because we don't yet know "d", and therefore we should pick the y-intercept (0,3). Since 20 equals 1, subbing (0, 3) into y=a2dx+6 gives us that a=-3.
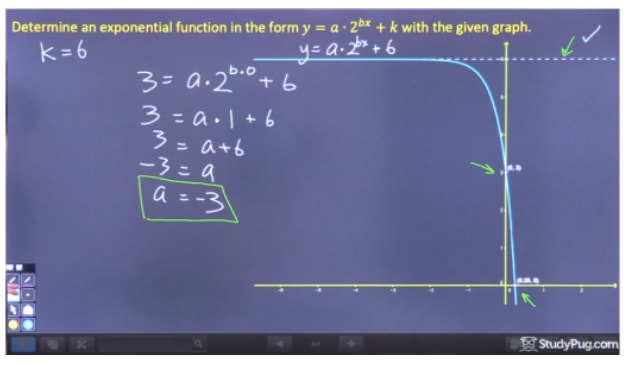
Step 3: Solve for "b"
Now that we have "a" and "k", all we have to do is pick another point and solve for b. Let's pick the point (0.25, 0). With all this information, we can find that d=4.

Step 4: Write the Final Equation
Now we that we have found all of the necessary variables, all that's left is to write out our final equation in the form y=abdx+k. Our final answer is y=(−3)24x+6

And that's it for exponential functions! Again, these functions are a little more complex than equations for lines or parabolas, so be sure to do lots of practice problems to get a hang of the new variables and techniques. With more practice, soon exponential equations and the graphs of exponential functions will be no trouble at all!
remaining today
remaining today



