Solving linear systems using Cramer's Rule
All in One PlaceEverything you need for better marks in university, secondary, and primary classes. | Learn with EaseWe’ve mastered courses for WA, NSW, QLD, SA, and VIC, so you can study with confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
0/2
Intros
Lessons
0/7
Examples
Lessons
- Cramer's Rule with 2 x 2 matrices
Solve the following linear systems with Cramer's Rule" - Cramer's Rule with 3 x 3 matrices
Solve the following linear systems with Cramer's Rule"
Free to Join!
StudyPug is a learning help platform covering maths and science from primary all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Last chapter we saw that we are able to solve linear systems with Gaussian Elimination. Now we are going to take a look at a new method which involves solving linear systems with Cramer's Rule. Cramer's Rule requires us to find the determinant of 2 x 2 and 3 x 3 matrices (depends on your linear system). However, this rule can only be used if you have the same number of equations and variables. If you have a different number of equations and variables, then finding the determinant will be impossible. Hence, it will not be possible to use Cramer's rule.
Solving linear systems using Cramers Rule
What is Cramers rule
Cramers rule is a technique to solve systems of linear equations where there are the same amount of unknowns as equations in the system. The technique consists on a set of equations involving determinants and ratios in order to obtain the unique set of solutions for a linear system.
Throughout this lesson we will focus on explaining the method for solving a system that we will call Cramers rule 3x3 and Cramers rule 2x2, this means that we will focus on the cases where we have a system of equations with 3 equations for 3 unknowns (n=3) or a system with 2 equations for 2 unknowns (n=2). The reason for it is that Cramers rule is not practical when a system is of higher order than 3, other methods, such as solving a linear system with matrices using Gaussian elimination, or simply solving systems of linear equations by substitution are much more computationally effective to work through a linear system. Still Cramers rule is an important piece of linear algebra to be considered due its mathematical rigor and the deep understanding of the transcription of linear systems into matrices, and viceversa, when such systems have unique solutions.
How to use Cramers rule
But what is Cramers rule perse? Instead of reciting a Cramers rule definition, let us showcase the technique a little better by going through its steps in detail.
Steps to follow when using Cramers rule linear algebra:
1. For a linear system of three equations and three unknowns and for a linear system of two equations and two unknowns, as the ones represented below:
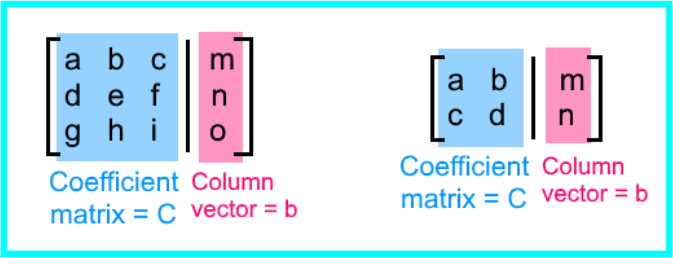
2. The system of linear equations has to be converted into and augmented matrix.
- From the augmented matrix, the elements in the left hand side of the vertical line which represents the equal sign conform a square coefficient matrix. This square coefficient matrix will be used to obtain a series of determinants in our next step.
- From the augmented matrix, the elements on the column vector on the right hand side of the equal sign will be used as replacement for certain elements when obtaining the set of determinants in the next step.
- The augmented matrices for the system with three equations and 3 unknowns and the system of two equations and two unknowns represented in equation 1 look as follows:
- Take into account that Cramers rule can be used with any system of n equations for n unknowns (as long as there are as many equations as unknowns, it doesnt matter the quantity). We have picked to represent the cases in which n=3 and n=2 since those are usually the ones used before we decide to continue our calculations with a different and more convenient technique.
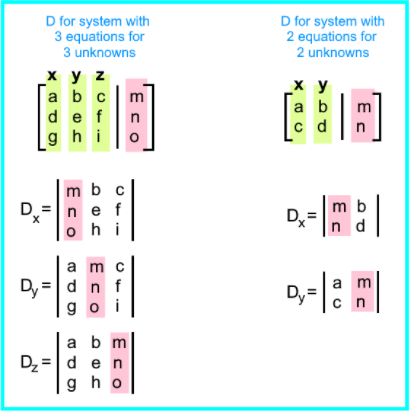
3. Then we need to calculate n+1 determinants.
- In other words, for the case in which n=3, we will be calculating 4 determinants. For the case in which n=2, we will calculate 3 determinants.
- The determinants are all named based in the variables contained in the system of linear equations in question. For example, for the case in which the system has three unknowns, you have variables x, y, z, therefore, the determinants are: Dx, Dy, Dz. For the case in which the system has two unknowns, you have the variables x, y, therefore, the determinants are: Dx, Dy. Besides, in each case, there is always an extra determinant we just call D.
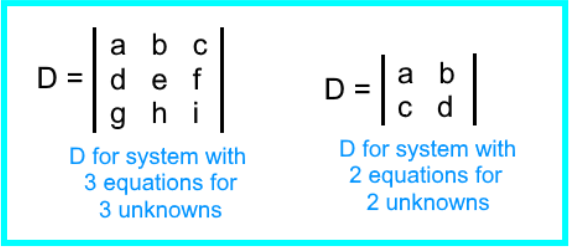
- The determinant D, is always the determinant of the square coefficient matrix (which we called C) from the left hand side of the augmented matrix. For the systems where n=3 and n=2. The determinant D would be as follows:
- The determinants Dx, Dy, Dz... are obtained by replacing the column vector b from equation 2, into the corresponding column on the square coefficient matrix.
4. Once the determinants have been calculated, we just follow the next ratio equations in order to obtain the values of the variables from the systems of equations:
In general, each equation for each variable, as shown in equation 5, is what we call the Cramers rule formula. Many books and published materials refer to this simply as Cramers rule, when in reality the technique requires multiple equations. For that same reason, sometimes you may see this technique called the matrix Cramers rule (usually referring to the augmented matrix from equation 2 or the set of determinants from equations 3 and 4).
As you can see, solving systems of equations using Cramers rule becomes very tedious very fast, and this is why this method is usually left on the side and people prefer to use techniques such as row reduction through gaussian elimination. If we compare such two methods, we can clearly see that as the system increases in number of equations, and thus unknowns, the Cramers rule matrices get bigger and the method longer since it requires n+1 amount of determinants to be solved; not only that, the determinants become bigger as n increases too.
Therefore, we are going to focus on solving systems of linear equations with up to 3 equations for 3 unknowns on this lesson, higher n values are suggested to be solved with other techniques for solving systems of linear equations.
Cramers rule to solve system of equations
Having explained the steps on how to do Cramers rule, let us learn how to use it while solving systems of linear equations.
We will divide this section in two parts, one dedicated to solve a system of 2 equations for 2 unknowns (n=2) and the other one dedicated to solve a system with 3 equations for 3 unknowns.
- Cramers rule for 2x2
Use Cramers rule to solve the system of 2 linear equations for 2 unknowns as shown below:
We convert the system into an augmented matrix:
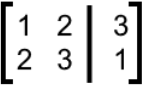
And then we calculate the 3 required determinants (remember that step 3 of our method dictates that we need to compute n+1 determinants. For this case we have a system of 2 unknowns, thus n=2, therefore n+1=2+1=3, and so, 3 determinants to be solved).
Following equation 3, we solve the Cramers rule determinant D first:
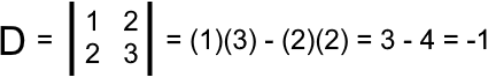
Notice how this determinant D is just the determinant of the square coefficient matrix from the left hand side of the augmented matrix in equation 7.
Now, to solve the determinants related to each of the variables in the equations from the system we need to substitute the column related to each variable in the square coefficient matrix, by the column coming from the right hand side of the augmented matrix. Thus, the determinants Dx, Dy are:
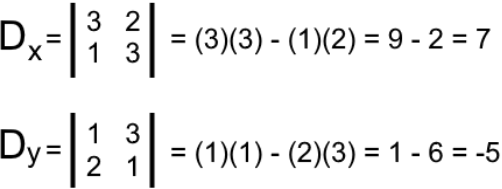
To finally find the unique solution for each variable in the equations, we now solve the Cramers rule equation for each of them:
And so, the system has been solved! The solutions for the variables x and y are: x=−7,y=5.
Now let us take a look at the process on how to do the Cramers rule 3x3!
- Cramers rule for 3x3
Use Cramers rule to solve the system of equations for 3 unknowns as shown below:
We convert the system into an augmented matrix:
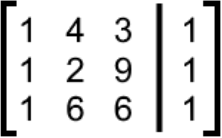
And then we calculate the 4 required determinants. Starting with determinant D:
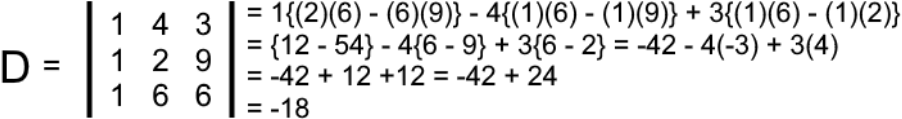
This determinant D is just the determinant of the square coefficient matrix from the left hand side of the augmented matrix in equation 12.
Now, to solve the determinants related to each of the variables in the equations from the system we substitute the column related to each variable in the square coefficient matrix by the column coming from the right hand side of the augmented matrix. And so, the determinants Dx, Dy, Dz are:
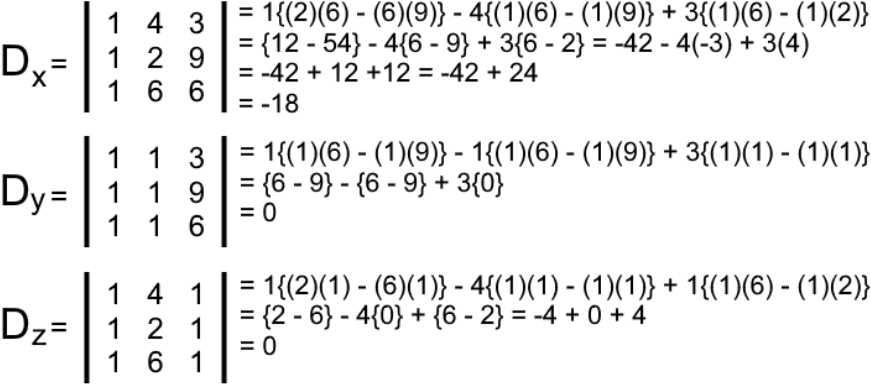
Solving for the variables x, y and z:
And so, the system has been solved! x=1,y=0,z=0
In summary, in order to use Cramers rule for solving linear equations we: rewrite the system into an augmented matrix, use the left hand side of this matrix as a square coefficient matrix, and the right hand side as a substitution for the solumns related to each variable in the coefficient matrix, set up the n+1 determinants for the system, evaluate determinants and apply Cramers rule equations to find the unique solutions to the variables.
Remember, if you are not completely content with this technique you can always work through a Cramers rule proof by solving the system using any of the other techniques you already know to solve linear systems of equations.
Cramers rule examples
On this section we add a few other examples exercises where we use Cramers rule to solve systems of equations. We start with a few examples of 2x2 systems and end up with a 3x3 problem.
Example 1
Solve the following linear system using Cramers rule:We convert the system into an augmented matrix:
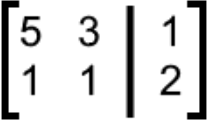
And then we calculate the 3 required determinants:
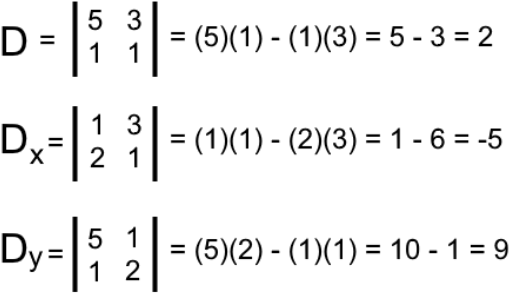
Now use D, Dx, Dy to finally find the unique solution for each variable in the equations:
So, the solutions for the variables x and y are: x=−2.5,y=4.5
Example 2
Solve the following linear system using Cramers rule:We convert the system given above to the standard notation so we can transform it into the augmented matrix later:
We convert the system into an augmented matrix:
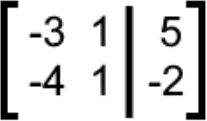
And then we calculate the 3 required determinants:
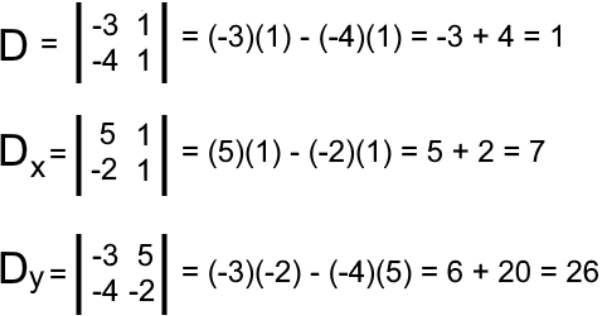
Now use D, Dx, Dy to finally find the unique solution for each variable in the equations:
So, the solutions for the variables x and y are: x=7,y=26
Example 3
Solve the following linear system using Cramers rule:We convert the system into the Cramers rule matrix (augmented matrix):
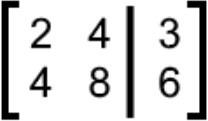
And then we calculate the 3 required determinants:
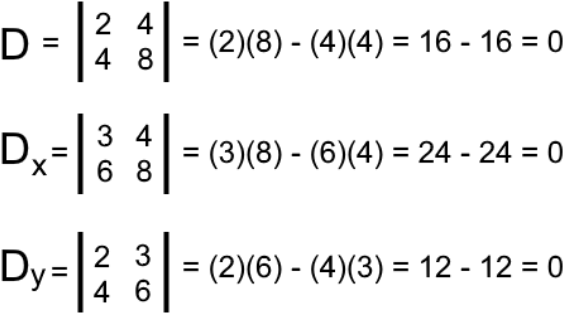
Now use D, Dx, Dy to finally find the unique solution for each variable in the equations:
So, the solutions for the variables x and y are: x=0,y=0
Example 4
For the final Cramers rule example, we will be solving a system of 3 equations for 3 unknowns:We convert the system into an augmented matrix:
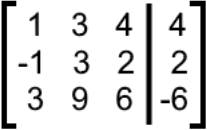
And then we calculate the 4 required determinants:

Now use D, Dx, Dy to finally find the unique solution for each variable in the equations:
And the system is solved! The solutions for the variables x, y and z are: x=−2,y=−2,z=3
For this last exercise we would like to work on a proof of Cramers rule by solving the system from equation 24 using another method and check for the result.
Thus, we use substitution to solve the system:
Now we continue the substitution technique by substituting the found value of the variable z into the first and second equations and obtain a new simplified system of 2 equations for 2 unknowns:
Using these new expressions found in equation 29, solve for x in the second equation and substitute it in the first equation to find y:
And we finalize this by substituting the found value of y into the second expression from equation 29:
The final found values for the variables x,y and z are: x=−2,y=−2,z=3
Therefore, the unique solutions for the variables in the linear system of equations match with the answers found using Cramers rule for matrices! And you can clearly see that both approaches are good for us to use when solving systems.
To finalize our lesson of today, as always, we have a few recommendations for your further studies. First, this detailed article in which you can find an example of using Cramers rule to solve two equations with two unknowns. And then, this link on the inverse matrix and Cramers rule where you can find an example of a 3x3 system in the bottom.
This is it for this lesson, see you in the next one!
This is a different way of solving linear systems. Instead of using Gaussian Eliminations, you can use Cramer's Rule! Make sure to review your determinants of 2 x 2 and 3 x 3 matrices.
Cramer's Rule for 2 x 2 matrices:
x=DDx
y=DDy
Cramer's Rule for 3 x 3 matrices:
x=DDx
y=DDy
z=DDz
Cramer's Rule for 2 x 2 matrices:
x=DDx
y=DDy
Cramer's Rule for 3 x 3 matrices:
x=DDx
y=DDy
z=DDz
Basic Concepts
- Solving a linear system with matrices using Gaussian elimination
- Solving a linear system with matrices using Gaussian elimination
- The determinant of a 2 x 2 matrix
- The determinant of a 2 x 2 matrix
- The determinant of a 3 x 3 matrix (General & Shortcut Method)
- The determinant of a 3 x 3 matrix (General & Shortcut Method)
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today



