Trigonometric ratios of angles in radians
All in One PlaceEverything you need for better marks in university, secondary, and primary classes. | Learn with EaseWe’ve mastered courses for WA, NSW, QLD, SA, and VIC, so you can study with confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Common Trigonometric Ratios
What are Trigonometric Ratios?
In the world of calculus, pre-calculus, and trigonometry, trigonometric ratios are a powerful and commonly used tool. With proper understanding, they are very easy to use as well!
In order to understand trigonometric ratios, let's first look back on some basic trigonometry principles. First, the Pythagorean Theorem with right triangles, and SOHCAHTOA. If you recall, we can use the Pythagorean Theorem (a2+b2=c2) to solve for unknown side lengths of right triangles, and we can use SOHCAHTOA to find missing angles. Below are the formulas we get from SOHCAHTOA, as well as an image to help you visualize it:
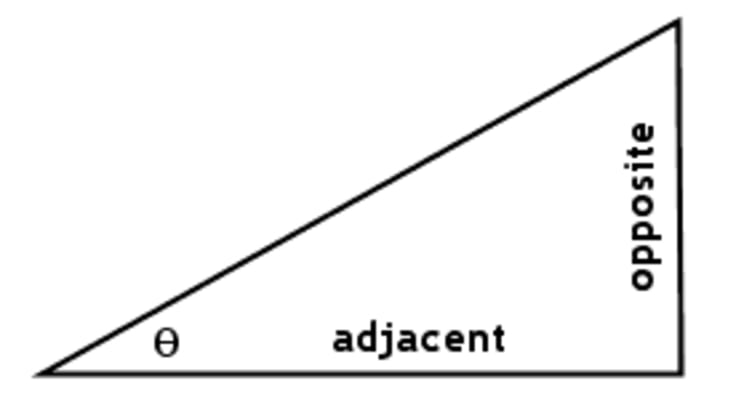
Using all of this information, as we further our study into pre-calculus and trigonometry, we will encounter what are known as "trigonometric ratios" – that is, simply just using SOHCAHTOA for important and commonly encountered angles.
Common Trigonometric Ratios:
Now, let's use the above recalled information to look at what trigonometric ratios are in concrete terms. Below is a table that summarizes the most important trigonometric ratios for sinx,cosx,tanx,cscx,secx, and cotx.
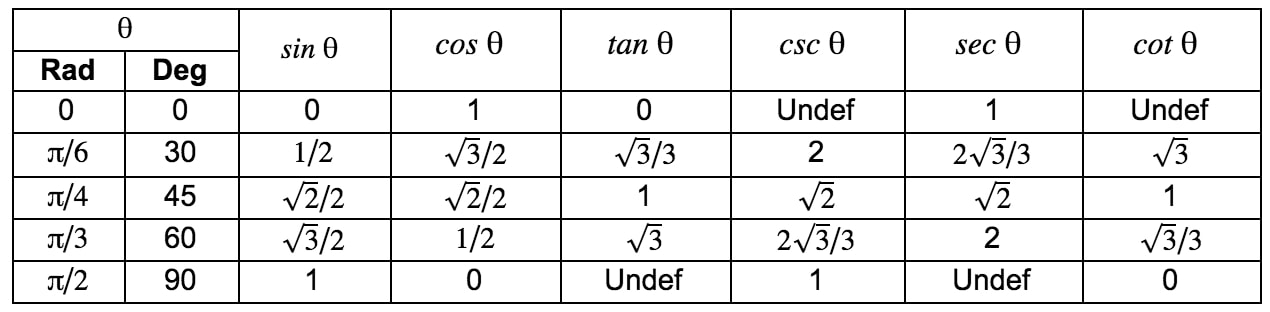
This above trig chart gives all the unit circle values for the first quadrant. As you can see, angles are listed in degrees and in radians. You should know both, but you're most likely to be solving problems in radians. Now, the next natural question is, how can I remember these trigonometric ratios? The answer – memorization, and a few helpful little tricks.
How to Find Trigonometric Ratios:
Memorizing the common trigonometric ratios in the table above is actually much easier than you would think. Though we can't completely forego memorization, we can make our lives a little easier using this one, incredibly useful trick.
Trick:
Because of the following 4 equations, we only need to memorize the unit circle values for sine and cosine.
With these 4 equations, we don't even need to memorize the trig ratios with tan, cot, sec, or csc! Of course, this recommendation will make questions take longer to solve. So, if you're aiming for speed, try memorizing the whole trig chart above!
Now that we have an idea of how to handle trig ratios, the best way to get comfortable with them is to solve some trigonometry problems.
Solving Trigonometric Equations:
Example 1:
Find cos0+sin2π+sec0
Step 1: Evaluate Trigs Individually
First, let's focus on radians. Let's assume we have only memorized the trigonometric ratios for sin and cos. With this assumption, we know we can easily evaluate the first two trig ratios cos0 and sin2π. The third ratio, sec0, however, requires an extra step using the trick we discussed earlier.
Step 2: Solve
Now that we've evaluated all of the trig ratios, all we have to do is solve the simple expression above.
Example 2:
Find sin90+cos90−tan60
Step 1: Evaluate Trigs Individually
Now let's focus on degrees. Again, let's assume we have only memorized the trigonometric ratios for sin and cos. With this assumption, we know we can again easily evaluate the first two trig ratios easily. The third ratio, however, requires the same trick we used in the previous question, but in this case on tan60 degrees.
Step 2: Solve
Now that we've evaluated all of the trig ratios, all we have to do is solve the simple expression above. Though we try to avoid the use of calculators when using trig ratios, we can certainly use one in this case.
Example 3:
Find tan3π+tan2π+sec4π
Step 1: Evaluate Trigs Individually
For the last example, let's try something a bit more challenging. Again, let's assume we have only memorized the trigonometric ratios for sin and cos. With this assumption, we are still unable to find any of the trig ratios without using our trick, so we have to a bit more work.
Step 2: Solve
Now that we've evaluated all of the trig ratios, all we have to do is solve the expression above. However, in this case, it is important to notice that our equation is unsolvable. Since we can't divide by zero, all we need to write in this case is:
And that's it! Hopefully you can now appreciate the simple power of trigonometric ratios. For more practice, visit this link here.
Basic Concepts
remaining today
remaining today



