Volumes of solid of revolution - Shell method
All in One PlaceEverything you need for better marks in university, secondary, and primary classes. | Learn with EaseWe’ve mastered courses for WA, NSW, QLD, SA, and VIC, so you can study with confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
- Find the volume of the solid obtained by rotating the region bounded by the x-axis and y=3x−x4 about the y-axis
- Find the volume of the solid obtained by rotating the positive region bounded by y=x3, y=x
- Use the Shell Method to find the volume of the solid obtained by rotating about the x-axis the region under y=x3 from x=0 to x=2
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Shell Method
Shell method (also known as the method of cylindrical shells) is another method that is used in finding the volume a solid. To be more precise, shell method is used when the rotation of the function creates cylinder-like shells as the cross section. Once you get the area of the cylindrical shells, then integrating it will give us the volume of the solid. It is similar to the disk method and washer method because it involves solids of revolution, but the process in using shell's method is slightly different. The Shell Method formula is one of:

where r is the radius and h is the height. The first one is used for shell method around y axis, and the second one is shell method around x axis. Shell method can even be used for rotations around specific x and y values.
The interesting thing is that if we were to integrate the area of the cylindrical shell, then we actually get the volume of cylinder. Look at
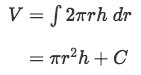
Ignoring the constant of integration, we see πr2 h is the cylinder volume formula.
Now here is a question you are probably asking. Why do we introduce another method? This is because there some cases where the disc method (or washer method) actually fails, and cannot calculate the volume of a solid. Let me give you an example.
Shell Method With Y Axis Rotation
Question 1: Find the volume of the solid obtained by rotating the region bounded by the x-axis and the following curve about the y-axis.

Since we are dealing with two functions (x-axis and the curve), we are going to use the washer method here. Recall that the washer method formula for y-axis rotation is:
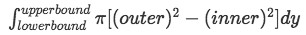
Where outer is the outer radius of the circle, and inner is the inner radius of the circle.
Notice that the curve looks like this:

Rotating it around the y-axis will show us the inner radius and outer radius

However, notice that both the inner radius and outer radius occur on the same function. So if we were to use the washer-method formula, then

Obviously the volume is not 0, so the washer method fails here. Now let's actually do the question with shell method.
-
Since the region is bounded by the x-axis and the curve, then we would like to find the intersection to get the bounds. Notice that the x-axis is the equation
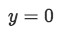
Equation 1: Shell Method about y axis pt.6 -
So setting y=0 and the curve equal gives:
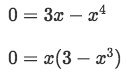
Equation 1: Shell Method about y axis pt.7 -
We see that the solutions for x are
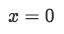
Equation 1: Shell Method about y axis pt.8 And
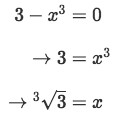
Equation 1: Shell Method about y axis pt.9 -
So our lower bound will be a 0 and the upper bound will be the cube root of 3. Now drawing the curves and plotting those bounds gives us the following graph:

Graph 3: Shell Method about y axis pt.10 -
Now what were going to do is rotate this around the y-axis, and show you how to imagine the cylindrical shell.

Graph 4: Shell Method about y axis pt.11 -
Notice the slice of cylindrical shell in the middle. Of course that is not the only cylindrical shell you can draw, you can actually have an infinite amount of shells stacked together. The point is that if you were to stack all these cylindrical shells, then you would get the volume of the solid. Recall that shell method formula for around the y axis is

Equation 1: Shell Method about y axis pt.12 Notice how the radius of the cylinder depends on x. In addition, the height of the cylinder is between the x-axis and the curve. Hence we can say that:
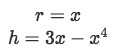
Equation 1: Shell Method about y axis pt.13 -
Plugging everything in our shell method formula gives us:
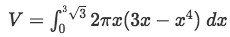
Equation 1: Shell Method about y axis pt.14 -
Factoring 2π out of the integral and distributing x gives:
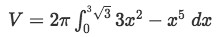
Equation 1: Shell Method about y axis pt.15 -
Integrating and evaluating gives:
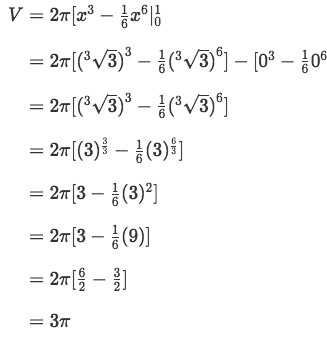
Equation 1: Shell Method about y axis pt.16
So this is how shell method integration looks like around the y-axis, but what around the x-axis? Let's do a question with that.
Shell Method With X Axis Rotation
Question 2: Find the volume of the solid by rotating the positive region bounded by
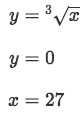
-
First, let's take a look at the region we are bounded by:

Graph 5: Shell Method about x axis pt.2 -
Note that the formula for the shell method around x-axis is:
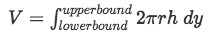
Equation 2: Shell Method about x axis pt.3 -
Notice the dy here. This means we have to make sure that everything is in terms of y. So changing our curve in terms of y will lead us to have:
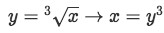
Equation 2: Shell Method about x axis pt.4 -
Our upper bound and lower bound also have to be in terms of y. Looking at the region we just drew we see that the lower bound is at y=0, and the upper bound is the intersection between x=27 and x=y^3. Solving for the intersection we see that:
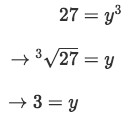
Equation 2: Shell Method about x axis pt.5 -
So the upper bound is 3. Now what is the radius and height? We need to look at what the graph looks like when it is rotated around the x axis.

Graph 6: Shell Method about x axis pt.6 -
Notice that the cylindrical shell is now sideways. The radius of the circle depends on y (r=y), and the height of the cylindrical shell is between
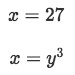
Equation 2: Shell Method about x axis pt.7 So the height would be the subtraction of the two. In other words,
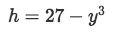
Equation 2: Shell Method about x axis pt.8 -
Now we have everything to plug into the formula.
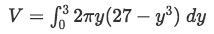
Equation 2: Shell Method about x axis pt.9 -
Integrating and evaluating we have that:

Equation 2: Shell Method about x axis pt.11 which is the volume of the solid.
Factoring 2π out of the integral and distributing the y we have:
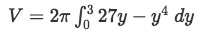
Note that this question can also be solved from using the disk method. Recall the disk method formula for x-axis rotations
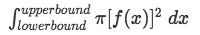
-
The bounds are different here because they are in terms of x. However from the graph we see that the lower bound is x=0 and upper bound is x=27. So plugging everything we have:
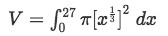
Equation 3: Disk method about x axis pt.2 -
Factoring π out of the integral and multiplying the exponents we have:
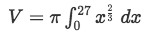
Equation 3: Disk method about x axis pt.3 -
Integrating gives us:
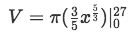
Equation 3: Disk method about x axis pt.4 -
Evaluating will give us:
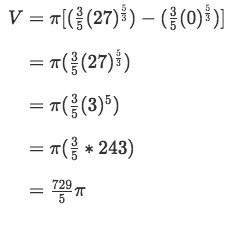
Equation 3: Disk method about x axis pt.5
As you can see, we get the same answer. Hence, both shell and disk method works here.
Shell Method with X-Value Rotation
Let's take a look at a question which involves rotation around a specific x value.
Question 3: Find the volume of the solid obtained by rotating the positive region bounded by
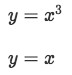
About x=2
-
First of all, let's draw the curves and see where the region is.

Graph 7: Shell Method about x value pt.2 -
Note when x=0, then
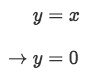
Equation 4: Shell Method about x value pt.4 And when x=1, then
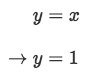
Equation 4: Shell Method about x value pt.5 -
So we have the points (0,0) and (1,1). Putting these in our graph we will have the following:

Graph 8: Shell Method about x value pt.6 -
Now we are going to rotate this graph around x=2.

Graph 9: Shell Method about x value pt.7 You can see that from the rotation, we can visualize cylindrical shells that are facing upward. We can also see that radius of this cylinder will be difference of 2 and the y=x curve. The height of cylinder will be the difference between the two curves. In other words,

Equation 4: Shell Method about x value pt.8 -
If you didn't understand why the radius and height are those equations, then you might be able to see it in the next graph.

Graph 10: Shell Method about x value pt.9 -
Notice how everything is in terms of x. Therefore our lower bounds and upper bounds should be in terms of x as well. So in this case, the lower bound is x=0 and the upper bound is x=1. Recall the shell method formula in terms of x is:

Equation 4: Shell Method about x value pt.10 -
Plugging everything in we have:
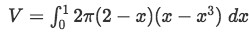
Equation 4: Shell Method about x value pt.11 -
Factoring 2π out of the integral and distributing we have:
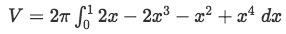
Equation 4: Shell Method about x value pt.12 -
Integrating and evaluating gives:
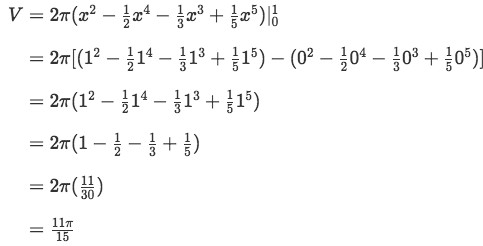
Equation 4: Shell Method about x value pt.13 which is the volume of the solid. Keep in mind that this is also solvable with washer's method.
So that is the positive region, but what are the bounds in integrating this region? We need to find the intersections of the curves to determine that. Setting the two curves equal to each other we have:
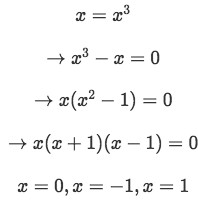
However notice that we are only dealing with positive regions, so we are going to exclude x=-1. Hence, the two x values are x=0, and x=1.
If you want to look at more examples of finding the volume of solid using the shell method, then I suggest you look at this link.
http://tutorial.math.lamar.edu/Classes/CalcI/VolumeWithCylinder.aspx
Paul covers a lot of questions using the shell method
remaining today
remaining today



