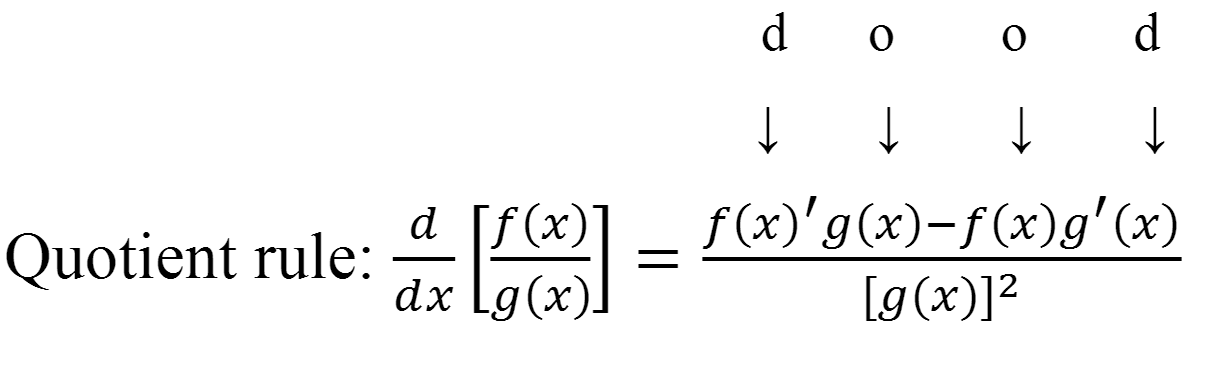Quotient rule
All in One PlaceEverything you need for better marks in university, secondary, and primary classes. | Learn with EaseWe’ve mastered courses for WA, NSW, QLD, SA, and VIC, so you can study with confidence. | Instant and Unlimited HelpGet the best tips, walkthroughs, and practice questions. |