Difference quotient: applications of functions
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Lessons
Examples
Lessons
- Find the Difference Quotient for: Linear Function
Find the difference quotient: f(x)=2x+5 - Find the Difference Quotient for: Polynomial Function
Find the difference quotient: - Find the Difference Quotient for: Rational Function
Find the difference quotient: - Find the Difference Quotient for: Radical Function
Find the difference quotient: f(x)=x
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Difference Quotient
What is the Difference Quotient?
Before we define the difference quotient and the difference quotient formula, it is important to first understand the definition of derivatives.
In the most basic sense, a derivative is a measure of a function's rate of change. That is, the instantaneous rate of change at a given point. In order to measure this value, we use what is called a tangent line, and measure its slope to given the best possible linear approximation at a single point.
In this article, however, we won't be looking at derivatives in particular. Instead, we will be looking at the difference quotient, which is a stepping stone to calculating derivatives of functions. The difference quotient allows us to compute the slope of secant lines. A secant line is nearly the same as a tangent line, but it instead goes through at least two points on a function.
In order to understand what the difference quotient is, it helps to visualize two points on a line like the following image:

If we recall the definition of slope, we can use this definition to find the "secant line" going through two points. Furthermore, if we use the variable "h" to represent the difference between the two x-values, we start to see a formula developing:
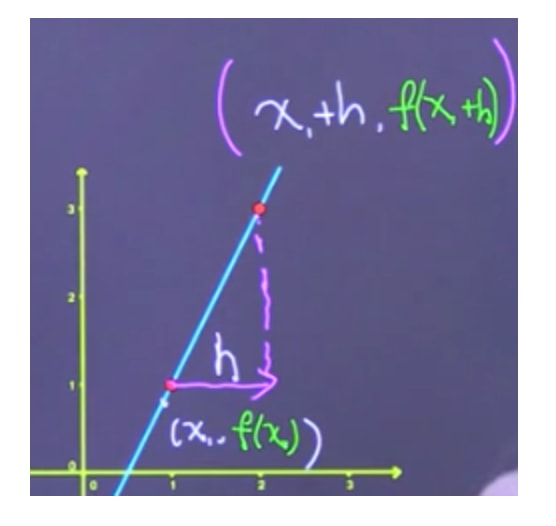
Finally, with some cancelling of terms, we can arrive at the very definition of the difference quotient.

Therefore, the formula for the difference quotient is:
Note: f(x) and f(a) are the same thing, and are just different notations for writing the formula. "h" still represents the difference between a or x-values.
This theory holds true for all functions, even though we derived it from a line. Therefore, this is the only difference quotient formula you need to know!
When using the difference quotient, several questions types can be asked. Most often, the questions found will be either to set up a difference quotient for a given function or to simplify hf(a+h)−f(a) for each function. Luckily, it is very easy to set up and use, once you are familiar with it. It is most difficult to simplify with rational functions and radical functions, but still more than manageable with lots of practice!
As always, the best way to practice this is to take a look at some example problems. But, before we do that, make sure you're comfortable with some basic operations with functions by checking out our videos on function notation, dividing functions, composite functions, and the slope equation . Having mastery of all of these techniques will make learning how to use the difference quotient much much easier!
How to Find the Difference Quotient:
In the most basic sense, setting up the difference quotient just involves subbing in the proper terms into the formula hf(a+h)−f(a). However, to make the process easier, it is best to take a good look at the given equation to make sure it is in the simplest form possible. Below is an example of what this means:
As you can see, when trying to sub in terms into the difference quotient formula, the first equation will be much easier than the second. This is because the second equation involves a lot more operations, and the addition of "h" into that mix makes errors much more likely. This will become more apparent as we get into some example problems.
Set Up a Difference Quotient for Linear Functions:
As it often goes, setting up the difference quotient is easiest for linear functions. For this kind of work, the less variables and the lower the degree, the easier it is!
Example 1:
Find the difference quotient of f(x)=2x+5
- STEP 1: Set Up Difference Quotient
In order to use the difference quotient, all we need to do is set f(a) equal to f(x), and make the necessary modifications to accommodate "h". It is very important to keep track of what is in the parentheses, as this is where it is most common to make mistakes! Once we do all this, we simply substitute what we need from f(x) to set up the difference quotient.
Here's the difference quotient formula again.
hf(a+h)−f(a)
Let's find f(x+h) by substituting (x + h) into f(x).
f(x+h)=2(x+h)+5
Then, we can plug f(x + h) and f(x) into the formula.
= h2(x+h)+5−(2x+5)
- STEP 2: Simplify
Once we have set up the difference quotient, all we need to do is expand whatever is in the brackets, collect like terms, and simplify!
h2(x+h)+5−(2x+5)
Expand the brackets, and collect like terms.
h2x+2h+5−2x−5=h2h
Now simplify the fraction by cancelling out h on the numerator and denominator.
= h2h=2
So we know the difference quotient of f(x)=2x+5 is 2
Set Up a Difference Quotient for Polynomial Functions:
Polynomial functions are of similar difficulty when it comes to finding the difference quotient. Again, as the degree (the highest exponent) of the polynomial gets higher, as does the difficulty. The most common difference quotient problems will deal with quadratic polynomial functions that have a degree of 2. Later, we will also look at a higher degree polynomial function by setting up a difference quotient for a cubic function.
Example 2:
Find the difference quotient of f(x)=x2+4x−6
- STEP 1: Set Up Difference Quotient
Again, in order to use the difference quotient, all we need to do is set f(a) equal to f(x), and make the necessary modifications to accommodate "h". Also remember it is very important to keep track of what is in the parentheses, as this is where it is most common to make mistakes! As an important side note, make sure you tackle these kinds of problem when the function is expanded out fully! If this function had been in factored form, it would have been much harder to set up the quotient.
hf(a+h)−f(a)
= h(x+h)2+4(x+h)−6−(x2+4x−6)
- STEP 2: Simplify
Just like last example, once we have set up the difference quotient, all we need to do is expand whatever is in the brackets, collect like terms, and simplify!
= h(x+h)2+4(x+h)−6−(x2+4x−6)
= hx2+2xh+h2+4x+4h−6−x2−4x+6
= h2xh+h2+4h
= hh(2x+h+4)
= 2x+h+4
Next, let's take a look at a more difficult polynomial by dealing with a cubic function.
Example 3:
Find the difference quotient of f(x)=x3−6x2+11x−6
- STEP 1: Set Up Difference Quotient
Just like with the quadratic function in the previous example, in order to use the difference quotient, all we need to do is set f(a) equal to f(x), and make the necessary modifications to accommodate "h". Also remember it is very important to keep track of what is in the parentheses, as this is where it is most common to make mistakes! This cannot be more important as we start dealing with more difficult equations and functions. Finally, just like the last example, make sure you set up the difference quotient for the function in its fully expanded form, i.e. not factored!

Set up difference quotient - STEP 2: Simplify
Once we have set up the difference quotient, all we need to do is expand whatever is in the brackets, collect like terms, and simplify! This is much more difficult compared to the quadratic example, as we have many more terms! Be sure to double and triple check your work. It is very easy to lose track of terms in these kinds of questions.
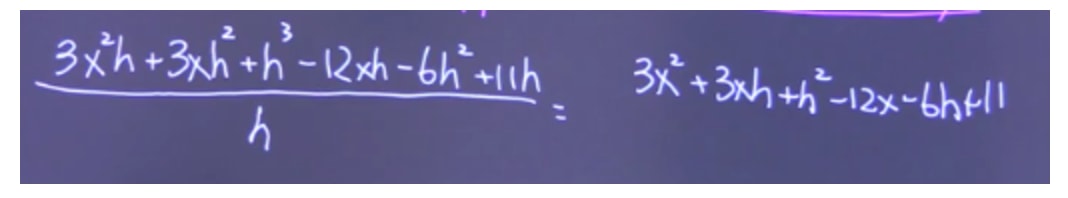
Simplify - Finally, we are left with the final answer of:
= 3x2+3xh+h2−12x−6h+11
As you can imagine, dealing with even higher-order polynomials can be quite the challenge. We won't cover anything more difficult than cubic functions in this article, but it wouldn't hurt to challenge yourself! Practice makes perfect.
Set Up a Difference Quotient for Rational Functions:
Polynomials and linear functions are often the simplest functions to deal with when doing problems on the difference quotient. The next sections cover rational and radical functions, which involve an extra level of difficulty.
Example 4:
Find the difference quotient of f(x)=x1
- STEP 1: Set Up Difference Quotient
Even though we have a rational function, which is a bit more tricky, the technique is still the same. In order to use the difference quotient, all we need to do is set f(a) equal to f(x), and make the necessary modifications to accommodate "h". Since we are using a rational function, you need to pay extra attention to detail to make sure everything is set up correctly.
hf(a+h)−f(a)
hx+h1−x1
- STEP 2: Simplify
Keeping in mind the careful attention we need to have, the procedure is still the same! All we need to do is expand whatever is in the brackets, collect like terms, and simplify!
hx+h1−x1
= hx+h1−x1∙x(x+h)x(x+h)
= hx(x+h)x−(x+h)
= hx(x+h)x−x−h
= hx(x+h)−h
= x(x+h)−1
This is the most basic rational function that exists, so, let's try something a little bit more difficult!
Example 5:
Find the difference quotient of f(x)=x+11
- STEP 1: Set Up Difference Quotient
Once again, even though we have a rational function, which is a bit more tricky, the technique is still the same. In order to use the difference quotient, all we need to do is set f(a) equal to f(x), and make the necessary modifications to accommodate "h". Since we are using a rational function, you need to pay extra attention to detail to make sure everything is set up correctly.
In this example, a slightly difference method is shown below. Instead of simply trying to input all values into the formula for the difference quotient, the first step is to instead find f(x+h) first. Once we know f(x+h), can can sub that into the difference quotient equation.

Set up difference quotient - STEP 2: Simplify
After the slightly different first step, the rest is the same. Keeping in mind the careful attention we need to have, all we need to do is expand whatever is in the brackets, collect like terms, and simplify! Then, we can easily find our final answer.
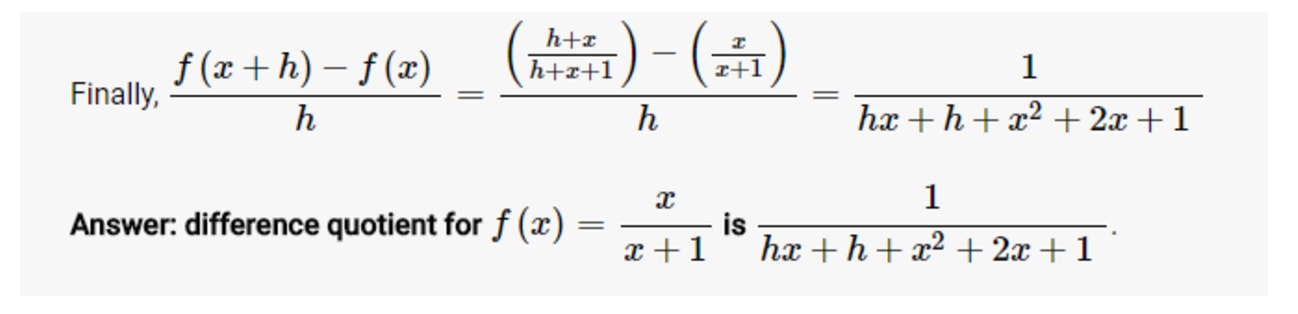
Simplify
Set Up a Difference Quotient for Radical Functions:
Last, but certainly not least, is finding the difference quotient for radical functions. By their very nature, radical functions are a bit more difficult than anything else. But, if we stay we the same technique we've been using since linear functions, nothing is all that different!
Example 6:
Find the difference quotient of f(x)=x
- STEP 1: Set Up Difference Quotient
Just like with rational functions, don't let the tricky nature of radical functions fool you. The procedure is the exact same. In order to use the difference quotient, all we need to do is set f(a) equal to f(x), and make the necessary modifications to accommodate "h". Also, since we are using a radical function, you need to pay extra attention to detail to make sure everything is set up correctly.
hf(x+h)−f(x) = hx+h−x
- STEP 2: Simplify
Paying careful attention to the root signs and all of our terms, all we need to do is expand whatever is in the brackets, collect like terms, and simplify! Then, we can easily find our final answer.
hx+h−x=hx+h−x∙x+h+xx+h+x
h(x+h+x)h=x+h+x1
And that's all there is to it! In this article, we have gone over the basic steps to solve any difference quotient problem. But, your studying is not done there! Be sure to practice with even more complex functions to make sure you have a firm understanding of this topic. To aid in your practice using the difference quotient, check out this great calculator here . Good luck!
remaining today
remaining today



