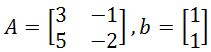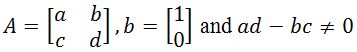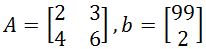Solving linear systems using 2 x 2 inverse matrices
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
Free to Join!
StudyPug is a learning help platform covering math and science from grade 4 all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Now that we learned how to solve linear systems with Gaussian Elimination and Cramer's Rule, we are going to use a different method. This method involves using 2 x 2 inverse matrices. To solve the linear system, we find the inverse of the 2 x 2 coefficient matrix (by using either row matrix operation or the formula) and multiply it with the answer column. Multiplying them would result in a column matrix, and the entries in the column matrix will give you a unique solution to the linear system.
Solving linear systems using 2x2 inverse matrices
On this lesson we will learn one of the uses of inverse matrices and their properties. You will notice how we can use them to make computations we are already familiarized with, but with a new approach, so get ready to have some more math fun.
How to solve systems of linear equations
In the past we have seen different methods to solve systems of linear equations, when studying general algebra we usually focus on the first three methods described below:- Solving linear systems by elimination
Solving systems of linear equations by elimination is one of the simplest methods to follow. The basic principle of this technique relies on adding or subtracting one equation from the other and thus quickly eliminate one of the variables, in that way reducing the amount of variables to solve for in a system. When only two unknown variables are present on a system, eliminating one by addition or subtraction of equations allows to solve for the one left in a straightforward manner. Although solving linear systems of equations through elimination is probably the simplest method, is not always the most practical, therefore, this technique is left for systems with equations that contain the same coefficient on one of their variables.
- Solving linear systems by substitution
The second method consists on solving systems of linear equations by substitution. Substitution means that we use one of the equations in the system to solve for one of its variables. Once you have an expression equal to the selected variable, you substitute this expression into the other equations in the place of the corresponding variable. By doing this you reduce the amount of unknown variables in the system, and if such system is composed of only two equations, you end up with an equation in terms of the other variable which can be solved quickly to its final result.
The substitution method is usually considered to be the most difficult out of the three options in general algebra, but as long as you follow the rule of: any operation done on one side of the equation, must be done to the other side this is the most used method by mathematicians. Substitution actually provides a basis for most of the algebraic methods to operate in any kind of mathematical function.
- Solving linear systems by graphing
Our third method refers to solving systems of linear equations by graphing where the solution is found when an ordered pair is shared between the two equations solutions. A shared ordered pair means that when both equations are graphed, they will intersect each other at a point and this point will be the shared ordered pair, thus this ordered pair will provide the solutions for x and y that correspond to such system.
Solving a system of linear equations algebraically is usually the most straightforward approach, no matter which of the first three methods you select to do it, but sometimes this is not possible since you may be provided with a linear system in matrix notation. For that we need to learn how to solve systems of linear equations using matrices.
- Solve linear systems through gaussian elimination:
In our lesson on solving a linear system with matrices using Gaussian elimination we introduced this technique (Gaussian elimination) which makes use of the three types of matrix row operations on an augmented matrix coming from a linear system in order to find the solutions for the unknown variables in such system. This technique is also called row reduction and it consists of two stages: Forward elimination and back substitution.
These two Gaussian elimination method steps are differentiated not by the operations you can use through them, but by the result each of them produces. The forward elimination step refers to the row reduction needed to simplify the matrix in question into its echelon form. Such stage has the purpose to demonstrate if the system of equations portrayed in the matrix have a unique possible solution, infinitely many solutions or just no solution at all. If found that the system has no solution, then there is no reason to continue row reducing the matrix through the next stage.
If is possible to obtain solutions for the variables involved in the linear system, then the Gaussian elimination with back substitution stage is carried through. This last step will produce a reduced echelon form of the matrix which in turn provides the general solution to the system of linear equations.
The only thing to remember when learning how to solve systems of linear equations through matrices and Gaussian elimination is that we can use the basic matrix row operations to arrive to the answer:
- Interchanging two rows
- Multiplying a row by a constant (any constant which is not zero)
- Adding a row to another row
Matrix inverses
In our lesson about the 2x2 invertible matrix we learnt that for an invertible matrix there is always another matrix which multiplied to the first, will produce the identity matrix of the same dimensions as them. In other words, an invertible matrix is that which has an inverse matrix related to it, and if both of them (the matrix and its inverse) are multiplied together (no matter in which order), the result will be an identity matrix of the same order. In general, the condition of invertibility for a nxn matrix A is:Therefore, if we define a 2x2 matrix X, the condition for the inverse 2x2 matrix is written as:
With that in mind, remember that if we define the 2x2 matrix X as shown below:
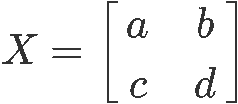
The determinant of a 2x2 matrix such as X can be written as:
Now, in order to understand what an inverse matrix equation is and learn how to solve a system of linear equations while we use the inverse to solve the system, we have to know how to obtain an inverse matrix.
When thinking on the expression X−1 the first idea that comes to mind is a division since an exponent of minus one in general algebra denotes a division of one by the number that has the exponent. The problem is that the operation of division using matrices does not exist given that a matrix is not a particular value, but a collection or array of multiple values, which geometrically speaking, do not even represent values in the same dimensional plane (depending on the dimensions of the matrix itself), so division by such a range of different variable characteristics cannot be defined and we say that matrix division is undefined.
This is where the concept of inversion comes to play an important role, and so, although not division perse, a matrix inversion comes to represent a related operation which will allow you to cancel out matrices when solving systems of equations or even simple matrix multiplications.
The formula for the inverse of a 2x2 matrix X is defined as:
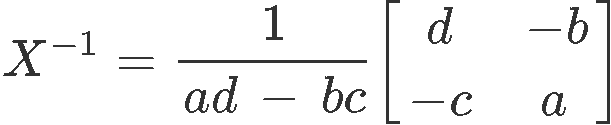
Notice that the first factor in the right hand side is composed by a division of one, by a subtraction of the multiplication of the matrix elements; this is in fact equal to have a factor of one divided by the determinant of the matrix. In later lessons you will see how this particular factor occurs in general in the formula for the inverse matrix of any size of matrices. But the question is, how do we use inverse matrix to solve system of equations? Let us find out!
Using inverse matrices to solve systems of equations
In our next lesson we will explain how we will be using inverse matrices to solve systems of equations. We basically follow the same logic as substitution in general algebra, but now our variables will represent matrices:
Imagine you have a matrix multiplication defined as A⋅B=C, where all A, B, and C are square matrices of the same order (same dimensions) and A and C are both known. Then you are asked to find out what the B matrix is.
Intuitively you will think about dividing out matrix A from both sides of the equation in order to cancel it out from the left hand side and solve for B; this is the method that we would use if they were regular variables after all, the problem is, these are matrices and division of matrices does not exist! What do we do? We obtain the inverse of matrix A and multiply it to both sides of the equation:
This particular solution allows us to observe how the inversion of matrices is the equivalent to divide one by a matrix, and thus, how it can be used to cancel out matrices in equations which require a division in a substitution-like solution method. Matrix B in equation 6 was solved thanks to us using our knowledge from equation 1: the multiplication of a matrix and its inverse, no matter in which order the factors are arranged, produces an identity matrix In of the same dimensions as the original matrices. Then, applying what we learnt in our lesson about the identity matrix, we know that any matrix multiplied by an identity matrix gives as a result the non-identity matrix itself. And so, we can conclude that B is equal to the inverse of A time C.
Examples of solving systems of equations using inverse matrices
For the following six example problems we are given matrices A and b. Knowing that vector x is defined as follows:
We need to solve the following linear systems by finding the inverse matrices of A in each case and using the equation: x=A−1b
Example 1
Having A and b defined as shown below: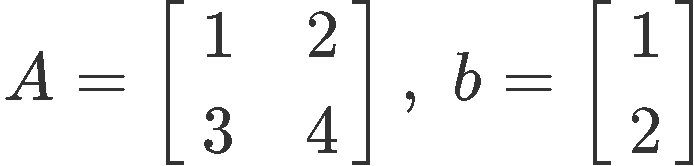
Solve system of equations using inverse matrix A−1. If you notice, throughout all of these example problems we will have to solve inverse matrices of A first, and if they are defined, we can then continue to solve for the values of x and y from the vector x.
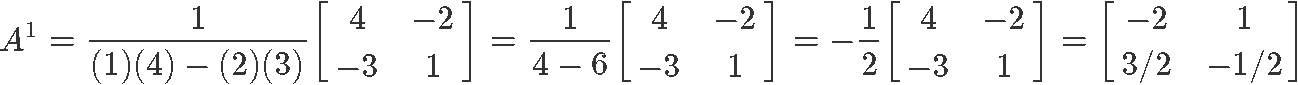
Having found the inverse matrix of A as shown in equation 9, we now use it as a factor in the matrix multiplication that defines vector x.
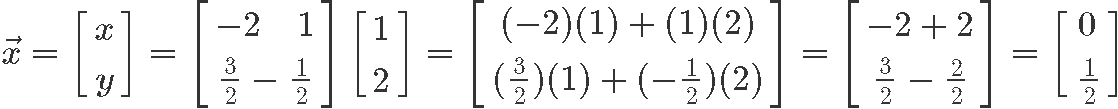
And so, the final values for x and y are: x=0 and y=21
Example 2
Having A and b defined as shown below: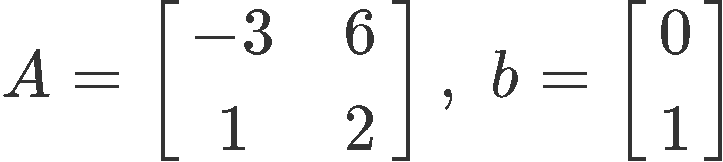
Solve the system using the inverse of the coefficient matrix A:
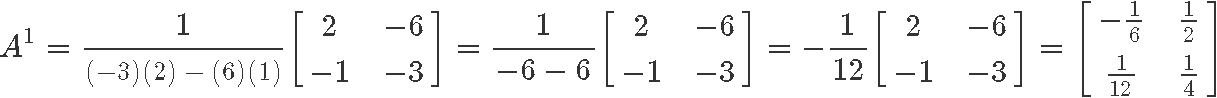
Solving for vector x:
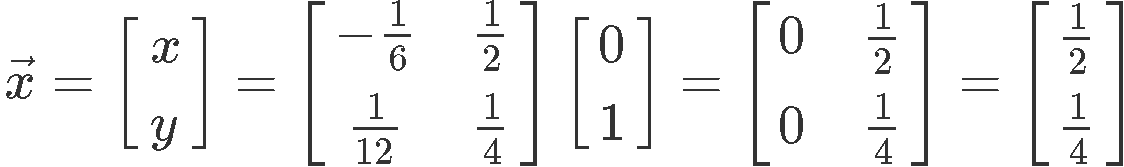
Therefore the values of x and y in this case are: x=21 and y=41.
Example 3
Having A and b defined as shown below: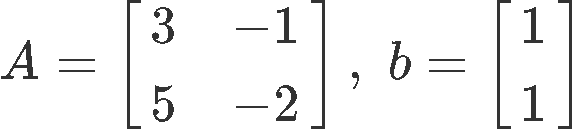
Obtaining the inverse matrix of A:

And then, using the inverse matrix to solve linear system x.

Thus the final values of x and y are:x=1 and y=2.
Example 4
Having A and b defined as shown below: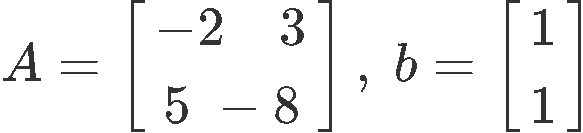
Obtaining the inverse of matrix A:
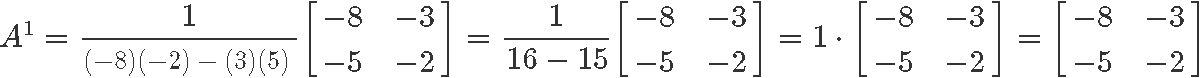
We use the given inverse to solve the system of equations which in this case is only representing vector x.
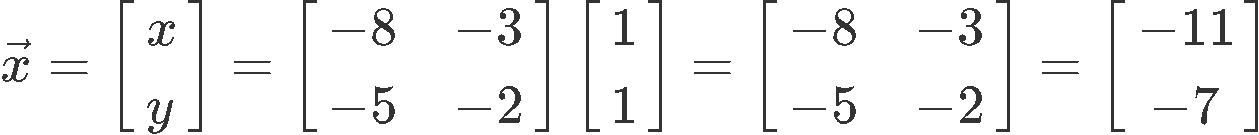
And so, the values for x and y in this case are: x=−11 and y=−7.
Example 5
Having A and b defined as shown below:
Calculating the inverse of matrix A:

Using the found inverse to compute the vector x.

The final values for x and y are: x=d and y=−c.
Example 6
Having A and b defined as shown below: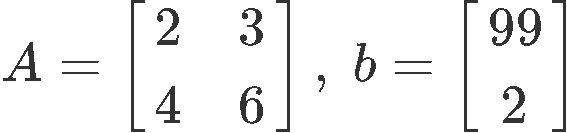
Finding the inverse of A:
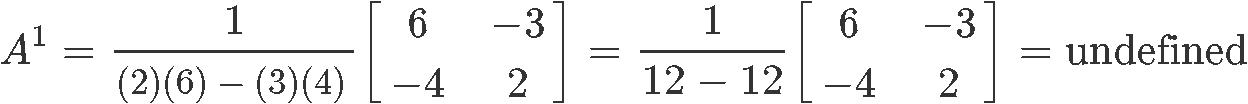
As you can see, there is no inverse. When this happens (inverse matrix is undefined), there is no way how to solve linear systems using inverse matrices so we have to resort to other methods (like the ones described in the first section of this lesson) to find the systems solution.
Having learnt the methods of solving systems of equations using inverse matrices, we finalize our lesson by providing a few recommendations of extra resources that can be useful to you.
This presentation on solving linear systems and the inverse matrix gives a similar approach as the one followed for this lesson, by following a continuous path for the different methods that can be used to solve these types of systems with matrices (regular and then inverse), so we think is a good read for you and extra reference. Our last recommendation is a little bit more broad, since the article contains general concepts the inverse of a square matrix. Still, at the end of the article you can read about the method for solving linear systems with inverses and this could be useful for you while doing independent study.
This is it for today, we hope you enjoyed our lesson and well see you in the next one!
Back then we learned that the linear system
1x+2y=3
4x+5y=6
Can be represented as the matrix
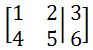
Now we can actually represent this in another way without the variables disappearing, which is
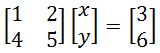
Now let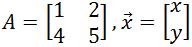 , and
, and 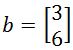 . Then we can shorten the equation to be
. Then we can shorten the equation to be 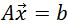 .
.
Now multiplying both sides of the equation by A−1 will give us
We know that A−1A=I, so then our equation becomes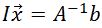 .
.
We also know that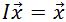 , and so our final equation is
, and so our final equation is
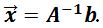
With this equation, we can solve (which has the variable x and y) simply by finding the inverse of A, and multiplying it by b.
(which has the variable x and y) simply by finding the inverse of A, and multiplying it by b.
4x+5y=6
Can be represented as the matrix
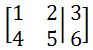
Now we can actually represent this in another way without the variables disappearing, which is
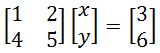
Now let
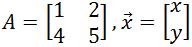 , and
, and 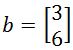 . Then we can shorten the equation to be
. Then we can shorten the equation to be 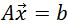 .
.Now multiplying both sides of the equation by A−1 will give us

We know that A−1A=I, so then our equation becomes
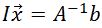 .
.We also know that
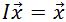 , and so our final equation is
, and so our final equation is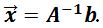
With this equation, we can solve
 (which has the variable x and y) simply by finding the inverse of A, and multiplying it by b.
(which has the variable x and y) simply by finding the inverse of A, and multiplying it by b.2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today

 , solve the following linear systems by finding the inverse matrices and using the equation
, solve the following linear systems by finding the inverse matrices and using the equation 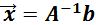 .
.