Properties of matrix multiplication
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
0/3
Intros
Lessons
0/13
Examples
Lessons
- Verifying the properties of matrix to matrix multiplication
You are given that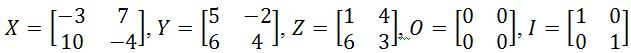 . Verify that:
. Verify that:
- Showing that the Commutative property fails
You are given that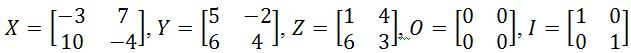 . Show that:
. Show that: - Dimension Property
You are given that X is a 2 x 4 matrix, Y is a 3 x 3 matrix, and Z is a 4 x 3 matrix. Are the following defined? If it is defined, show the dimensions of the matrix.
Free to Join!
StudyPug is a learning help platform covering math and science from grade 4 all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
In this section, we will learn about the properties of matrix to matrix multiplication. These properties include the associative property, distributive property, zero and identity matrix property, and the dimension property. You will notice that the commutative property fails for matrix to matrix multiplication. Lastly, you will also learn that multiplying a matrix with another matrix is not always defined. The product of the two matrices is only defined if the number of columns in the first matrix is equal to the number of rows in the second matrix.
Properties of matrix multiplication
A lot has been said and seen about matrix multiplication by now, at this time you already know how to multiply matrices (either among them, or with a scalar) and what type of results to expect; still, we would like to dedicate a complete lesson on the properties of it in order to show a few examples on how they can be used and how they reign this particular operations between two or more matrices.
How to multiply two matrices
Matrix multiplication is an operation descending from the dot product of vectors, since it actually consists in of a matrix dot product operation affecting an array of vectors performed in an orderly manner from a linear map described by the two (or more) matrices involved.This can be seen clearly in the next diagram, which at this point, you must very familiarized with:
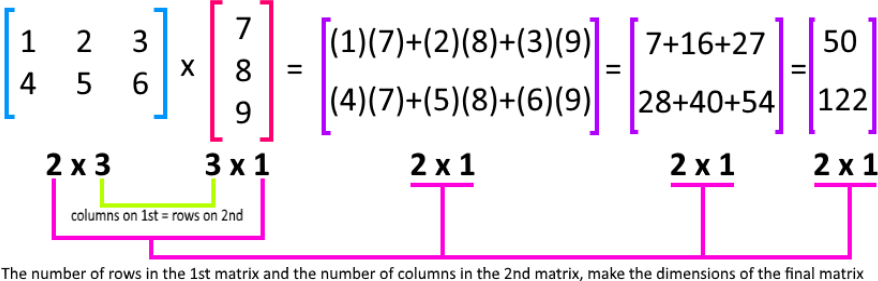
Just as explained in our lesson on matrix multiplication, the dot product occurring in this operation of matrices is the multiplication of each of the corresponding terms between a horizontal vector (row vectors from the rows of the first matrix) and a vertical vector (column vectors from the columns of the second matrix in the multiplication), and this same dot product occuring to produce each of the element entries of the resulting matrix.
A dot product is also called a scalar product because the result of two vectors in this manner is always a scalar number. For a matrix multiplication, the scalars resulting from each of the dot products described in the paragraph above happen to be the entries of the resulting matrix, hence, the way the multiplications of the row vectors with the columns vectors end up producing a matrix which may have a different set of dimensions as the original, but still a combination of them both, by always resulting with the same number of rows from the first matrix and the same number of columns as the second matrix (since the order in which the scalar products are performed is from the rows of the first matrix and the columns of the second).
In general, the dot products occurring while multiplying matrices can be seen in the right hand side of the equation below, producing the entries of the resulting matrix.
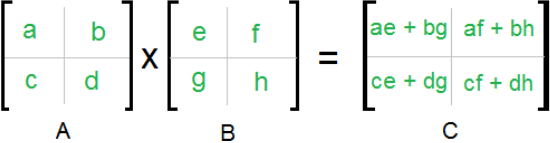
On equation 2 above we can see an example of a multiplication of two square matrices, notice the matrix properties of those involved will always affect the properties of the resulting matrix. For the case of multiplication of square matrices, the dimensions of the resulting matrix will be the same as those which produced it.
With that in mind, let us focus on learn about the specific properties of matrix multiplication in the next section.
Properties of matrix multiplication in linear algebra
Let X, Y, and Z be matrices, In be and identity matrix and 0n be a zero matrix. Now let all of these five matrices to be square matrices of the same order (same dimensions), the next matrix multiplication properties hold true:1. Dimension property for matrix multiplication
When multiplying two matrices the result is not always defined. Matrix multiplication rules tell us that in order for such multiplication to produce a defined resulting matrix, the first matrix must have the same amount of columns as the second matrix has rows. That being said, the dimensions of the resulting matrix will be defined by the amount of rows in the first matrix and the number of columns in the second matrix (check equation 1).
The dot product of matrices of the same size, which are square matrices such as in the case for the five defined matrices in this section, produces a matrix of the same size as those involved in the multiplication.
2. Associative property
The associative property of matrix multiplication gives the opportunity to perform a multiple-matrix multiplication in steps by associating together two matrices, performing their multiplication, and then using its result as a new factor instead of the two which generated it.
At the same time, the matrix multiplication associative rule allow us to select which set of matrices to multiply together first. Using the matrices X, Y and Z defined on this section, this associative property says that:
3. Distributive property
The distributive properties of matrix multiplication come to place when an operation of the matrix multiplication is combined with another arithmetic operation, such as an addition or subtraction. In other words, we use the distributive property to simplify problems in which one of the factors in the matrices multiplication is an addition or a subtraction of matrices.
Mathematically speaking the distributive property can be defined if two ways:
When a matrix is multiplying a factor containing either an addition of subtraction of two (or more) matrices. In which case the operation would look like:
Or, when a term containing an addition or subtraction of two (or more) matrices is multiplying a matrix:
Notice that in both cases the order in which the matrices are being multiplied is conserved, we will talk about this on the next section of our lesson, since is related to the lack of commutative properties of matrix multiplication. For now, a few details are worth mentioning: Since X, Y and Z are all square matrices of the same order (size), the resulting matrices will have the same dimensions as them, but if we were to use matrices of different dimensions, these multiplications would have to follow the property of dimension rules and the resulting matrices would have dimensions according to that.
4. Matrix to matrix multiplication property for the zero matrix
This property dictates that as long as the matrix product is defined, meaning that the multiplication follows the dimension properties and a result can be obtained, such result will always be the zero matrix itself. This rule applies to both scalar multiplication and matrix multiplication with matrices of any dimension, since as long as you have a zero matrix as a factor, the result will always end up being the zero matrix as long as the dimension property allows a result.
If you multiply matrices by a zero matrix or vice versa, the logic behind the operation is very simple. Given that all of the elements in a zero matrix are zeros, no matter which matrix you multiply to them, if a result can be defined it will produce a series of dot products by zero which will produce element entries equal to zero in the resulting matrix, and thus, a zero matrix.
So, if you multiply matrix X by the zero matrix (using the matrices defined at the beginning of this section), the result goes as follows:
5. Matrix to matrix multiplication property for the identity matrix
Similarly to the way how multiplying matrix X times the zero matrix works, the multiplication of a matrix times the identity matrix always gives the same result: the original matrix which is being multiplied to the identity.
In simple words, when multiplying a matrix times an identity matrix (making sure the product is defined by following the dimension property) the result will always be the original, non-identity, matrix, and so:
Which properties do not hold true for matrix multiplication
After studying the matrix multiplication properties above you may have noticed there is one property we have seen in other matrix operations which has not appeared here, and so, you may be wondering: Is matrix multiplication commutative? The short answer is NO, in general.Remember you can multiply matrices of different dimensions as long as the first matrix contains the same amount of columns as the number of rows in the second matrix. If you look at the multiplication shown in equation 1, you will clearly see how changing the order of the matrices in the operation will not be able to produce a result since the characteristic of the columns on first = rows on second is not met.
But the dimension rules are not the only reason why the factors in a matrix multiplication cannot be commuted, the same holds in general for square matrices, which would have no issue corresponding to their dimensions. The result of a matrix multiplication of square matrices will change, in general, if you exchange the order in which the matrices are being multiplied. The issue arises from the order in which the elements inside the matrices are being operated in dot products, since changing the order of the matrices, changes the order in which these multiplications take place (except for certain special cases) and thus, they produce different element entries in the resulting matrix. This is defined as:
More on this will be explained and verified during the example exercises in the last section of this lesson, for now, it is important for you to know that although the commutative property does not hold for matrix multiplication in general, there are two special cases in which it does: the matrix multiplication with the zero matrix, and the matrix multiplication with the identity matrix.
These two cases were explained in our last section, and will be verified in the exercises in the next section.
Properties of matrix multiplication PROOF
On this section we will work through a variety of example problems designed to verify the properties involved in how to do matrix multiplication.Example 1
On this problem we will verify the properties of matrix to matrix multiplication using the matrices defined below: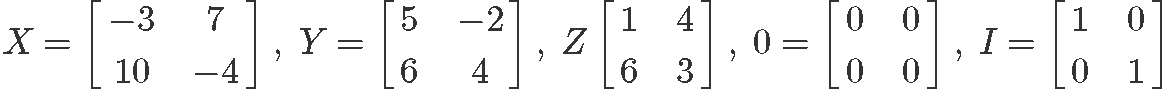
Using these, verify the following expressions and name the properties which are being proved.
1) (XY)Z=X(YZ
This expression is the same as Equation 3, and therefore, the question here is: is matrix multiplication associative? We know it is, so let us prove it using the matrices above. We start by calculating the left hand side: (XY)Z
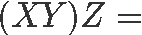
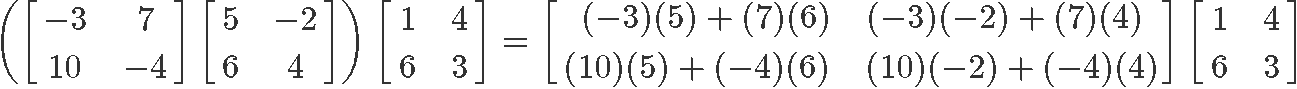
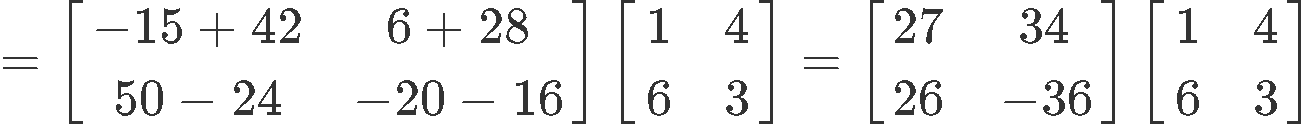
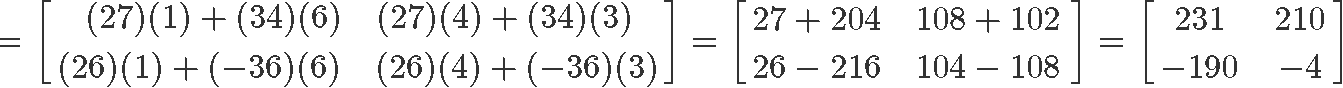
Now to compute the right hand side: X(YZ)
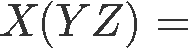
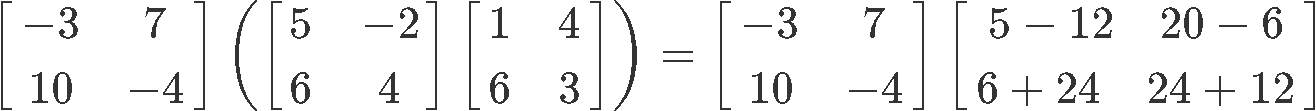
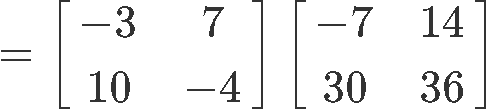
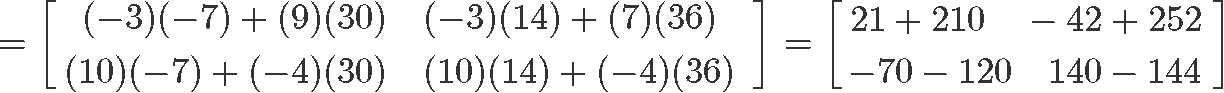
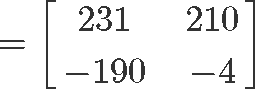
And so, we have proved that the associative property holds true.
2) X(Y+Z)=XY+XZ
The multiplication of matrix X with the addition of Y and Z is part of the distributive property of matrix multiplication, as shown in equation 4. Therefore, let us verify it, we start by computing the left hand side: X(Y+Z)
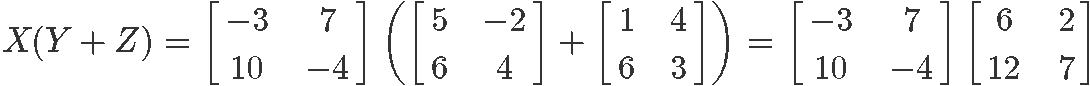
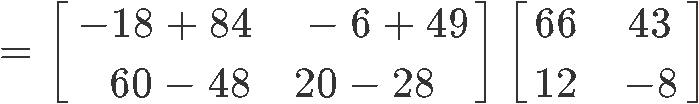
Now to compute the right hand side: XY+XZ
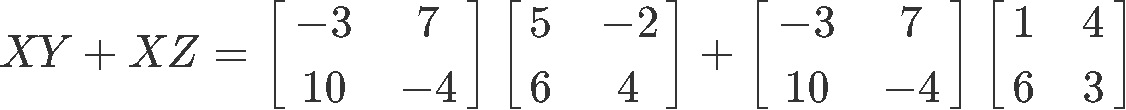
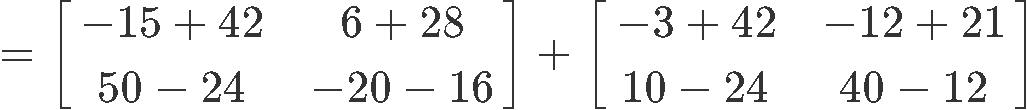
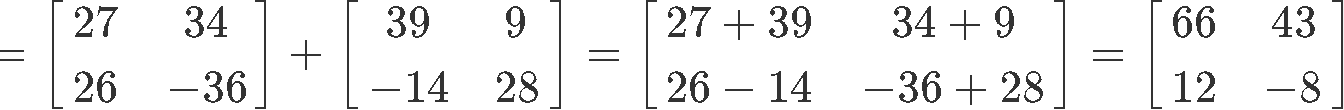
And so, we have proved that the distributive property holds true.
3) (Y+Z)X=YX+ZX
Once more, we are to verify the distributive property on this case, but now the associated with equation 5. So, calculating the left hand side: (Y+Z)X
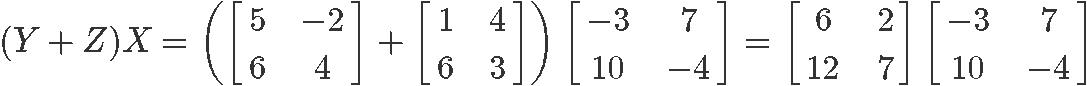
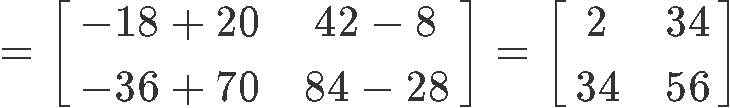
Computing the right hand side: YX+ZX
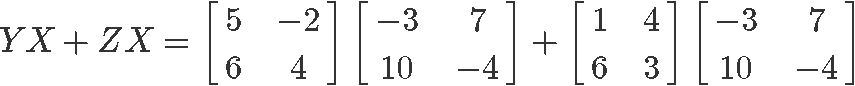
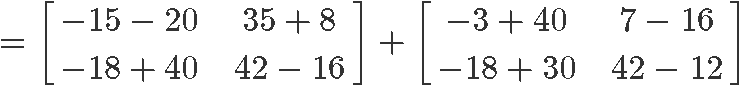
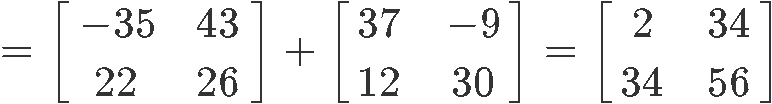
And so, we have proved that the distributive property holds true again.
4) OX=O
Performing the matrix multiplication 2x2 of the zero matrix 0 and X, we can easily observe that the result is a zero matrix equal to 0.
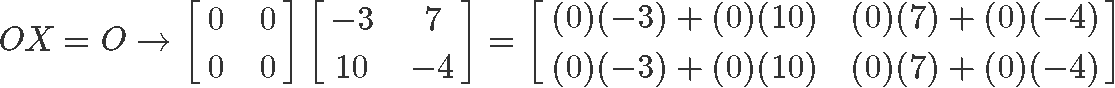
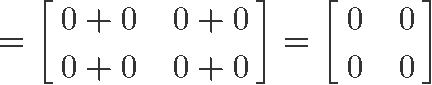
Thus, the matrix to matrix multiplication property for the zero matrix holds true as shown in equation 6.
5) IY=Y
Multiplying 2x2 matrices I and Y, we can easily observe that the result is equal to the non-identity matrix.
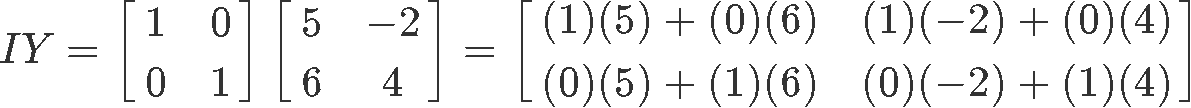
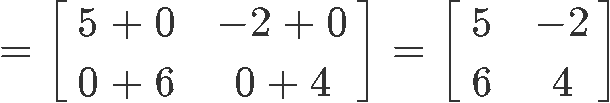
Thus, the matrix to matrix multiplication property for the identity matrix holds true as shown in equation 7.
Example 2
On this matrix multiplication example we will show how the commutative property fails in general for matrix multiplication operations. Once more having the five matrices X, Y, Z, 0 and I as shown below: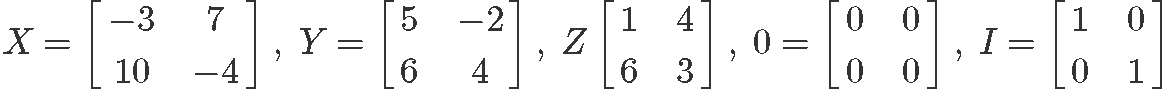
Verify the next expressions:
1) XY ≠ YX
Notice that dimensionally speaking there is no impediment for these two sides of the algebraic equation to be the same since both X and Y are square matrices of the same size, but, the elements inside them are multiplied in different order when the matrices get exchange, and so, the results of the multiplications in each side of this expression as not the same:
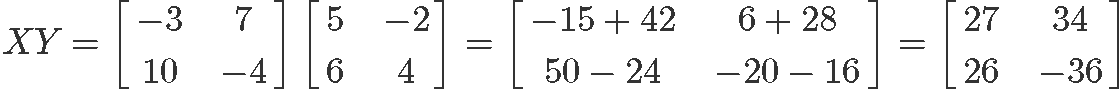
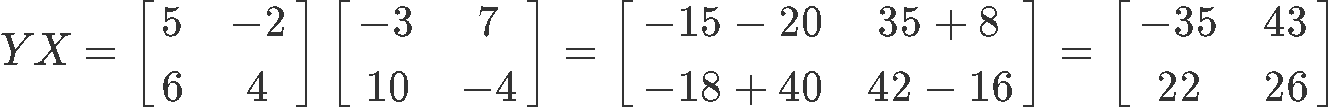
2) X(Y+Z ≠ (Y+Z)X
Just as before, the same happens on this example where the commutative property fails:
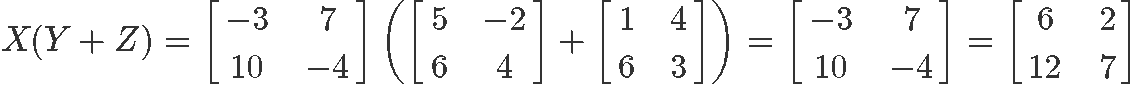
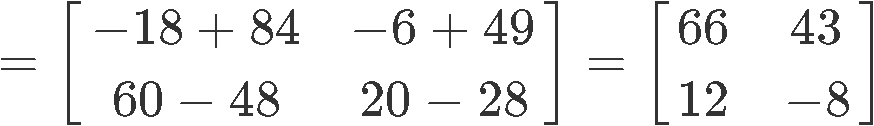
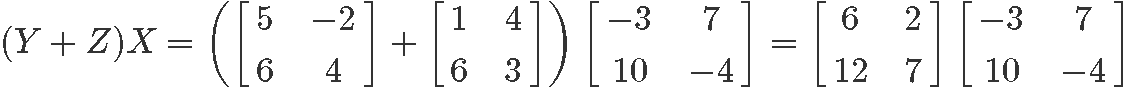
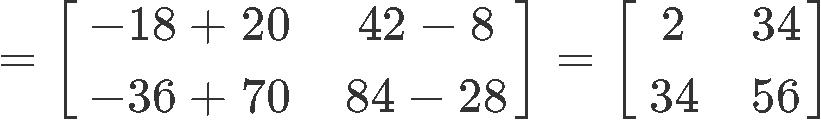
Example 3
Let us work with the dimension property of matrix multiplication for this example. Here, you are given a 2x4 matrix named X, a 3x3 matrix named Y and a 4x3 matrix named Z. Are the matrix multiplications in the expressions below defined? If defined, show the dimensions of the resulting matrix for each case.Note: Remember that the dimension property follows the rule: (A×B)(B×C)=(A×C)
Where A is equal to the amount of rows in the first matrix, B is the amount of columns in the first matrix which is equal to the amount of rows in the second matrix, and C is the amount of columns in the seconds matrix. Thus, the resulting matrix has the same number of rows as the first one, and the same number of columns as the second one.
1) XY
The expression describing the dimension relationship on this matrix multiplication goes as follows:
Notice the multiplication is undefined because X does not have the same number of columns as Y has rows.
2) XZ
The dimension relationship on this matrix multiplication is:
Since X has a matching number of columns with the rows in Z, the matrix can be performed with the dimensions in the resulting matrix being 2 × 3.
3) ZX
For this case, the dimension relationship for the matrices on this multiplication is:
Which is undefined due Z having a number of columns different than the number of rows in X.
4) ZY
Here, Z and Y have a matrix multiplication dimension relationship of:
Since Z has a matching number of columns with the rows in Y, the matrix can be performed with the dimensions in the resulting matrix being 4 × 3.
5) XZY
For this multiplication we will have to use the associative property to simplify into a 2-factor multiplication. The complete dimension relationship goes as:
As you can see, given this order in which the matrices are being multiplied there is a defined result, which is a matrix of dimensions 2 × 3.
6) ZYX
Using the associative property once more to simplify into a 2-factor multiplication. The complete dimension relationship of the matrix multiplication ZYX goes as:
Where the result is NOT defined due to the unmatching number of columns from the matrix resulting from ZY with the rows in matrix X.
As we finalize this lesson, we recommend you to visit the next link on the properties of matrix multiplication which contains some more problems for you to practice.
We hope you have enjoyed this lesson, see you in the next one!
Let X,Y,Z be matrices, In be an identity matrix, and On be a zero matrix. If all five of these matrices have equal dimensions, then we will have the following matrix to matrix multiplication properties:
Associative property
(XY)Z=X(YZ)
Distributive property
X(Y+Z)=XY+XZ
(Y+Z)X=YX+ZX
There are also some matrix to matrix multiplication properties with zero matrices and identity matrices.
Matrix to matrix multiplication property for the zero matrix
OX=O or XO=O
Matrix to matrix multiplication property for the identity matrix
XIn=X or InX=X
Here are some important things to know.
Commutative property fails: Notice that the commutative property fails when you use matrix to matrix multiplication. For example, XY=YX.
Dimension property: When multiplying a matrix with another matrix, it is not always defined. The product of the two matrices is only defined if the number of columns in the first matrix is equal to the number of rows of the second matrix.
Associative property
(XY)Z=X(YZ)
Distributive property
X(Y+Z)=XY+XZ
(Y+Z)X=YX+ZX
There are also some matrix to matrix multiplication properties with zero matrices and identity matrices.
Matrix to matrix multiplication property for the zero matrix
OX=O or XO=O
Matrix to matrix multiplication property for the identity matrix
XIn=X or InX=X
Here are some important things to know.
Commutative property fails: Notice that the commutative property fails when you use matrix to matrix multiplication. For example, XY=YX.
Dimension property: When multiplying a matrix with another matrix, it is not always defined. The product of the two matrices is only defined if the number of columns in the first matrix is equal to the number of rows of the second matrix.
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today



