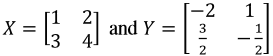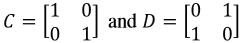Identity matrix
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Identity Matrix
Having learned about the zero matrix, it is time to study another type of matrix containing a constant specific set of values every time, is time for us to study the identity matrices.
What is an identity matrix?
An identity matrix is a given square matrix of any order which contains on its main diagonal elements with value of one, while the rest of the matrix elements are equal to zero.
To explain part by part this definition, let us start by reminding you that a square matrix refers to a matrix containing the same amount of rows and columns. The order of a matrix comes from its dimensions, and its main diagonal refers to the array of elements inside the matrix which form an inclined line from the top left corner to the bottom right corner. Given the characteristics of an identity matrix, we can also conclude these type of matrices are also diagonal matrices.
A diagonal matrix is that in which all of its element entries are equal to zero, except for the elements found on its main diagonal. In this case, all of the non-zero entries in the matrix will have a value of one, and that happens to be one of the reasons why the identity matrix is sometimes called the unit matrix too.For the case of matrix linear algebra notation, the identity matrix serves as the equivalent object to the unit in numerical algebra (other reason why is called the unit matrix). In other words, the identity matrix is the equivalent to the unit of one, but in this case it happens to be an algebraic object with dimensions and array organization which can be used in operations with other ordered number arrays (other matrices).
In the next section we will take a look into the properties of the identity matrix, and the unit matrix definition will make much more sense, especially in the case of matrix multiplications including an identity matrix (look at property number 3). Mathematically, the identity matrix is represented as:

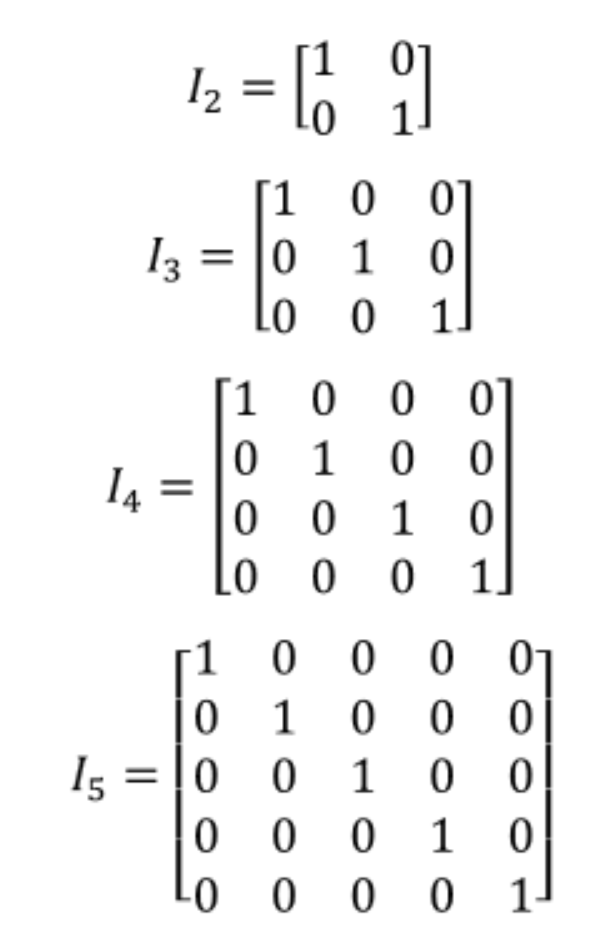
And so, in equation 2 we can easily see that I2 refers to an identity matrix with two rows and two columns, which at the same time has only two elements in its main diagonal; a notation of I3 corresponds to an identity matrix of order 3, or one containing three rows and three columns and 3 elements on its main diagonal; and the notation system continues that way for any subindex n.
Identity matrix properties
- An identity matrix is always an square matrix:
As seen in equations 1 and 2, the order of an identity matrix is always n, which refers to the dimensions nxn (meaning there is always the same amount of rows and columns in the matrix). - An identity matrix is capable of multiplying any matrix with any order (dimensions) as long as it follows the next rules:
- If in the multiplication, the identity matrix is the first factor, then the identity matrix must have dimensions with as many columns as the matrix it is multiplying has rows.
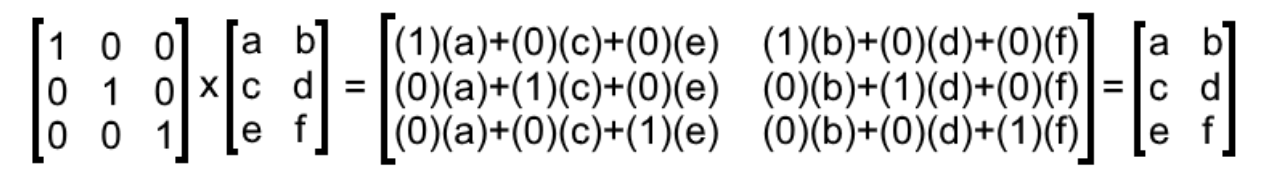
Equation 3: Multiplying an identity matrix times a non-unit matrix - If the identity matrix is the second factor in the multiplication, the identity matrix must have the same amount of rows as the matrix that is multiplying it has column
These two rules come from the conditions of matrix multiplication.

Equation 4: Multiplying a non-unit matrix times an identity matrix - As a result of the first two rules, If an identity matrix is multiplying a square matrix of the same dimensions, the result will also be a square matrix which will be the same as the non-unit matrix of the multiplication, no matter the order in which the matrices are being multiplied with one another.
- If in the multiplication, the identity matrix is the first factor, then the identity matrix must have dimensions with as many columns as the matrix it is multiplying has rows.
- Following the two equations from the second property explained above, from all the identity matrix properties, the main one can be observed clearly in equations 3 and 4: Whenever an identity matrix multiplies another matrix, and the multiplication can be solved (following the rules for matrix multiplication), the result is equal to the non-unit matrix involved. Mathematically speaking:
If you think about it, this is the equivalent to multiplying a regular real number by the unit (by one). Any number multiplied by one results in the same original number. The same goes for a matrix multiplied by an identity matrix, the result is always the same original non-identity (non-unit) matrix, and thus, as explained before, the identity matrix gets the nickname of "unit matrix".
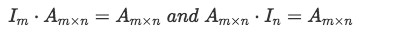
Equation 5: Multiplying an identity matrix times another matrix - Multiplying a matrix times its inverse will result in an identity matrix of the same order as the matrices being multiplied. Mathematically speaking:
The matrices involved in such multiplication are called multiplicative inverses of each other. We will leave the explanation about inverse matrices for later lessons, starting with the topic of the inverse of a 2x2 matrix. For now, it is just important that you know this is one of the properties of identity matrix that we can use to solve matrix equations.
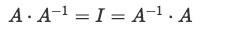
Equation 6: Multiplying a matrix by its inverse - The determinant of the identity matrix In is always 1, and its trace is equal to n.
Although we have not seen what a determinant is so far, for the moment is important to know that the reason a determinant of any identity matrix is equal to one is because the diagonal of these matrices contains only ones and the rest of the elements inside these matrices are zeros. We will introduce the concept of determinant in a later lesson called the determinant of a 2x2 matrix, where the identity matrix determinant will be explained in more detail.
On the other hand, the trace is much simpler to explain. By now you should know that the trace of a matrix refers to the addition of the elements found in its main diagonal. Since an identity matrix has diagonal elements all equal to one, when adding them all in order to obtain the trace, you will always have as many elements as the order of the identity matrix, which is n. Take the next identity matrix as an example:Equation 7 shows an identity matrix 3x3, thus n=3 for this matrix. In that way, the trace is the addition of the elements of its diagonal, which is three elements of value 1 added with one another, and so, the trace is equal to 3. Therefore, the trace of an identity matrix is equal to n.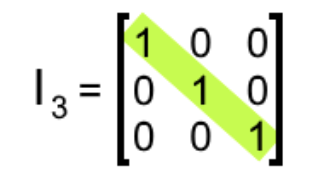
Equation 7: Example of an identity matrix of order 3x3 - For our last property we start with a question: is the identity matrix invertible? The answer is yes. We will explain more on this topic through our lesson on about the 2x2 invertible matrix, for now just remember: The inverse of the identity matrix is itself.
We can prove the inverse of identity matrix is itself by multiplying them together. Remember from our fourth property that multiplying a matrix by its inverse produces the identity matrix, and so, we have computed the corresponding multiplication for this case (shown in equation 8) and proved that the inverse of a 2x2 identity matrix is itself.

Equation 8: The identity matrix as inverse multiplicative of itself.
Identity matrix example problems
Making use of the properties learnt in the past section and the identity matrix definition given at the beginning of this lesson, solve the next example problems:
Example 1
Given the matrices below: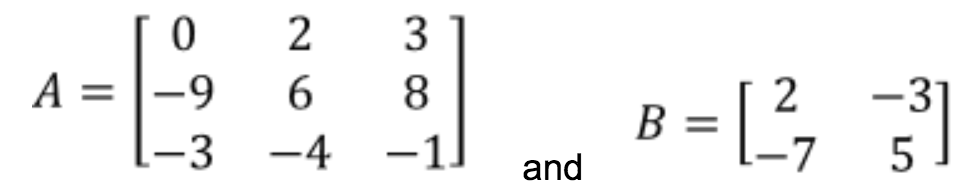
- I3⋅A
On this case we have an example of the third property of the identity matrix: A multiplication involving an identity matrix and any other matrix, if defined due the rules of matrix multiplication, the result is the non-unit matrix (for this case, matrix A). And so, this multiplication goes as follows: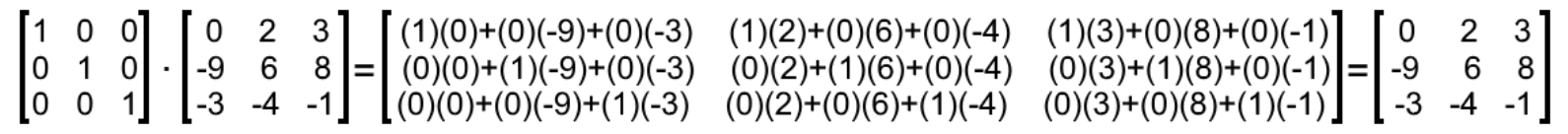
Equation 10: Matrix multiplication involving an identity matrix - 2A+4I3
For this matrix operation we are computing two cases of scalar multiplication, the second one including a 3x3 identity matrix. Solving such operation goes as: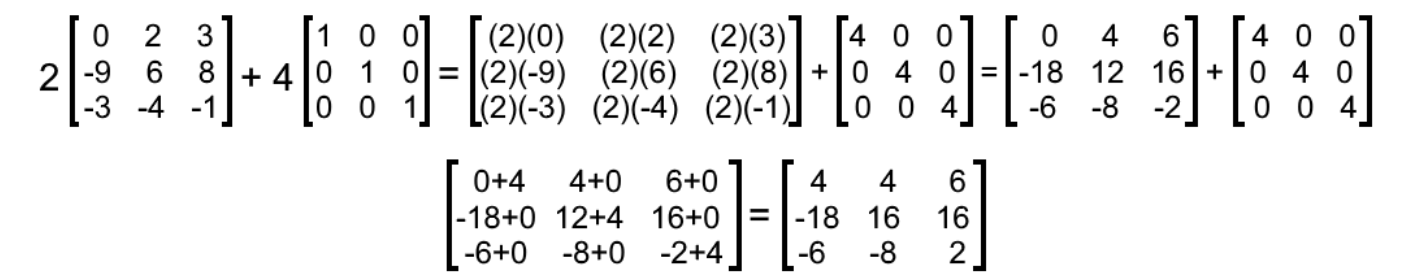
Equation 11: Addition of two scalar matrix multiplications - −4B+2I2
Once more, this operation consists on using an identity matrix for addition of two scalar multiplications, where the second multiplication includes an identity matrix 2x2. We solve them as shown below: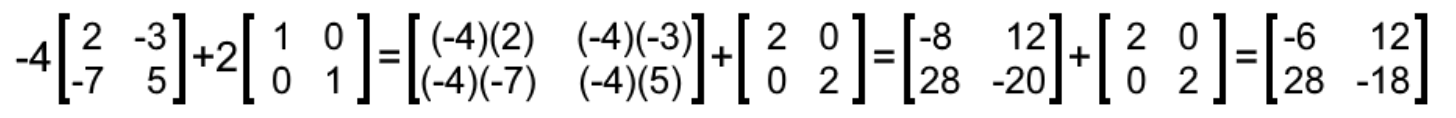
Equation 12: Addition of two scalar matrix multiplications - I2⋅B
By the third property, we know the result of this multiplication is matrix B: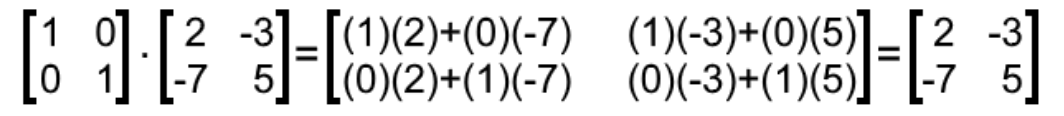
Equation 13: Multiplying a 2x2 identity matrix to another matrix of same order - 0⋅I4
On this case, we have a scalar multiplication of an identity matrix with the number zero, thus, the result must be a zero matrix as shown below: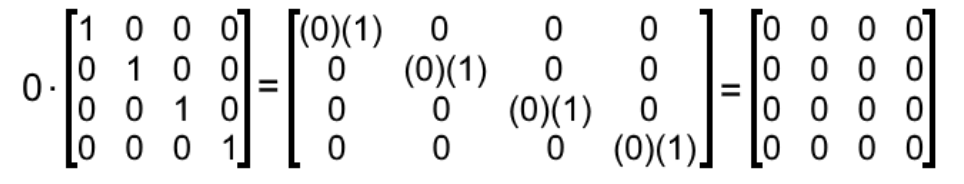
Equation 14: Scalar multiplication of an identity matrix producing a zero matrix
Example 2
Show if the following matrices are multiplicative inverses of each other:- Having matrices X and Y as shown below:
We perform the matrix multiplication of X ⋅ Y:
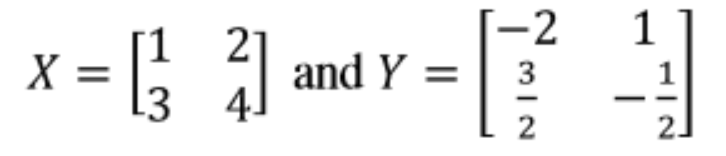
Equation 15: Matrices X and Y Given that the result is the identity matrix, we conclude that X and Y are multiplicative inverses of each other.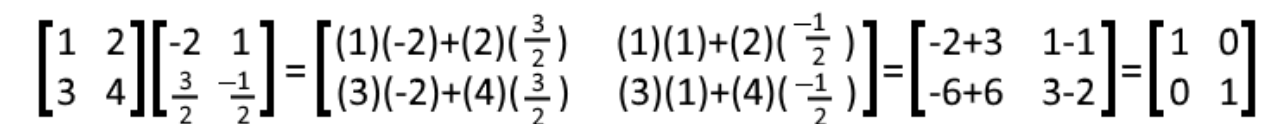
Equation 16: Multiplying matrices X and Y - Having matrices A and B as shown below:
We perform the matrix multiplication of A ⋅ B:
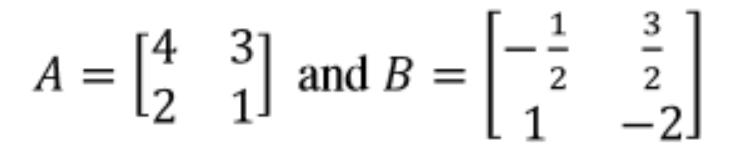
Equation 17: Matrices A and B Thus, A and B are multiplicative inverses of each other.
Equation 18: Multiplying matrices A and B - Having matrices C and D as shown below:
We perform the matrix multiplication of C ⋅ D:
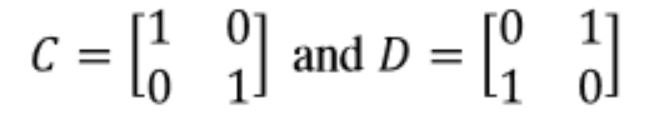
Equation 19: Matrices C and D Although very similar, the resulting matrix from the operation above is not an identity matrix. Therefore, this operation shows that C and D are NOT multiplicative inverses of each other.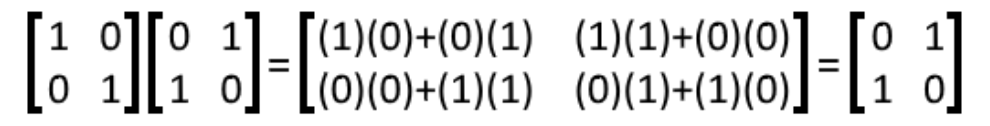
Equation 20: Multiplying matrices C and D - Having matrices E and F as shown below:
We perform the matrix multiplication of E ⋅ F:
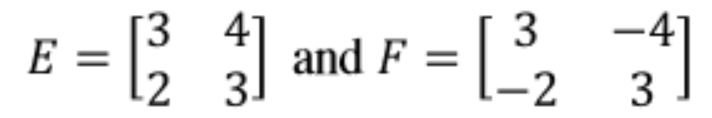
Equation 21: Matrices E and F Therefore, E and F are multiplicative inverses of each other.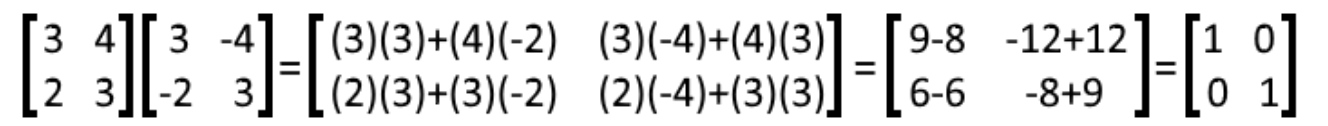
Equation 22: Multiplying matrices E and F
Before we go, let us recommend you the next little link defining the identity matrix in a concise manner, and this article which relates both topics of matrix multiplication and the identity matrix by talking about the commutative property of the multiplication of any square matrix with an identity matrix of the same order (just as described on the third property in section two of this lesson), and how this doesn't apply to other matrix multiplications.
So, this is it for today, see you in the next lesson!
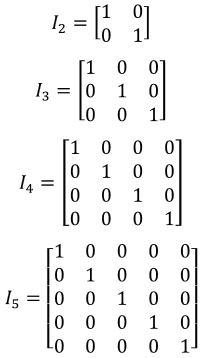
are all identity matrices.
remaining today
remaining today

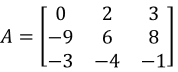 and
and 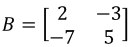 . Perform the following matrix operations:
. Perform the following matrix operations: