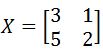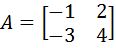The Inverse of a 2 x 2 matrix
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
0/2
Intros
Lessons
0/7
Examples
Lessons
Free to Join!
StudyPug is a learning help platform covering math and science from grade 4 all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
In this lesson, we will learn how to find the inverse of a 2 x 2 matrix. You will learn that if two matrices are inverses of each other, then the product of the two matrices will result in an identity matrix. Next, you will learn how to find the inverse by using the formula below. You may find that the formula is hard to memorize. There is another way to find a 2 x 2 matrix without memorizing the formula, but it would require matrix row operations. You will see this method in the section "the inverse of 3 x 3 matrices with matrix row operations". Lastly, note that the inverse of a 2 x 2 identity matrix is just the identity matrix itself.
The inverse of a 2x2 matrix
In our past lesson we learnt that for an invertible matrix there is always another matrix which multiplied to the first, will produce the identity matrix of the same dimensions as them.In other words, an invertible matrix is that which has an inverse matrix related to it, and if both of them (the matrix and its inverse) are multiplied together (no matter in which order), the result will be an identity matrix of the same order. In general, the condition of invertibility for a nxn matrix A is:
Therefore, if we define a 2x2 matrix X, the condition for the inverse 2x2 matrix is written as:
But how do you find the inverse of a 2x2 matrix? We go through the whole process to find the inverse of a 2x2 matrix in our first section for this lesson, and then we follow that concept by making the calculations which prove it is right in the second section. So get ready and lets have some math fun!
How to find the inverse of a 2x2 matrix
In order to know what is the inverse of a 2x2 matrix we must start by defining a second order matrix, such as matrix X shown below: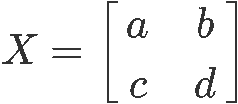
From our lesson on the the determinant of a 2x2 matrix we learnt that the determinant of X is mathematically defined as:
Now we need to find its matrix inverse X−1. When thinking on the expression X−1 the first idea that comes to mind is a division since an exponent of minus one in general algebra denotes a division of one by the number that has the exponent. The problem is that the operation of division using matrices does not exist given that a matrix is not a particular value, but a collection or array of multiple values, which geometrically speaking, do not even represent values in the same dimensional plane (depending on the dimensions of the matrix itself), so division by such a range of different variable characteristics cannot be defined and so we say that matrix division is undefined.
This is where the concept of inversion comes to play an important role, and so, although not division per se, a matrix inversion comes to represent a related operation which will allow you to cancel out matrices when solving systems of equations or even simple matrix multiplications.
The formula for the inverse of a 2x2 matrix X is defined as:
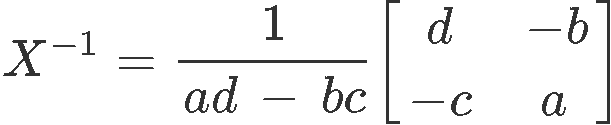
Notice that the first factor in the right hand side composed by a division of one by a subtraction of the multiplication of the matrix elements, is equal to have a factor of one divided by the determinant of the matrix. In later lessons you will see how this particular factor occurs in general in the formula for the inverse matrix of any size of matrices.
For now, we continue to focus on the inverse of a 2x2 matrix and the next question arises: Why is an inverse matrix important, and how can it be used?
Imagine you have a matrix multiplication defined as A⋅B=C, where all A, B, and C are square matrices of the same order (same dimensions) and A and C are both known. Then you are asked to find out what the B matrix is.
Intuitively you will think about dividing out matrix A from both sides of the equation in order to cancel it out from the left hand side and solve for B; this is the method that we would use if they were regular variables after all, the problem is, these are matrices and division of matrices does not exist! What do we do? We obtain the inverse of matrix A and multiply it to both sides of the equation:
This particular solution allows us to observe how the inversion of matrices is the equivalent to divide one by a matrix, and thus, how it can be used to cancel out matrices in equations which require a division. We have been able to solve for matrix B in equation 6 thanks to use our knowledge from equation 1: the multiplication of a matrix and its inverse, no matter in which order the factors are arranged, produces an identity matrix In of the same dimensions as the original matrices. Then, applying what we learnt in our lesson about the identity matrix, we know that any matrix multiplied by an identity matrix gives a result the non-identity matrix itself. And so, we can conclude that B is equal to the inverse of A time C.
Having learnt the usage and how to get the inverse of a 2x2 matrix, let us go next into a section dedicated to prove that equations 2 and 5 are correct, if other words, let us calculate the inverse of 2x2 matrix proof with an example given matrix so you can observe the formula for inverse of 2x2 matrix in action. Later, in our last section, we will work through a series of exercises in order for you to practice.
Inverse of a 2x2 matrix proof
On this section we will prove how a 2x2 matrix and its inverse meet the condition defined in equation 2. For that we define matrix A as shown below:
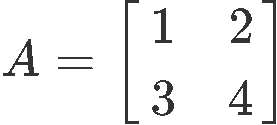
The first part of our proof is to verify this matrix is in fact an invertible matrix, for that, we obtain its determinant:
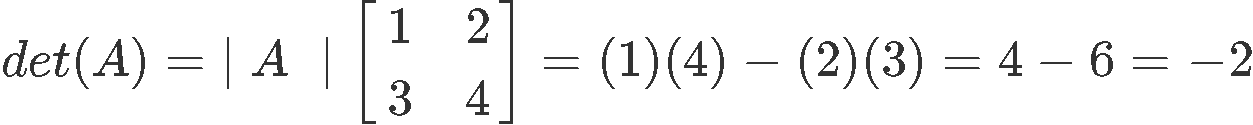
Since our matrix A has a determinant which is not equal to zero, we can determine A is an invertible matrix and so, we can finally calculate its inverse. For that, we use equation 5 and obtain:
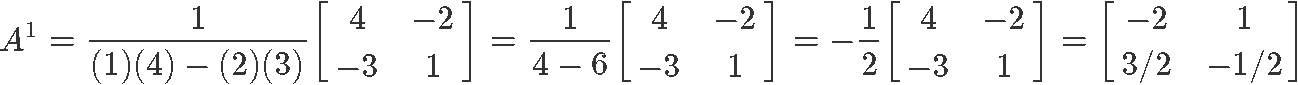
Hence, now we can finally prove the expression found in equation 2 by multiplying matrix A with is inverse.
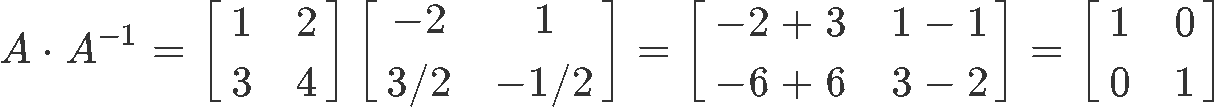
And so, as you can see, the matrix multiplication between matrix A and its inverse produces the identity matrix with the same dimensions as them. Therefore we have proved that the expressions providing the conditions for invertibility of a matrix (shown in both equation 1 and equation 2), hold true.
Remember the expression found in equation 1 provides de invertibility condition in general, meaning, it applies to square matrices of any order (dimensions). In later lessons we will look at how to compute the inverse of 3x3 matrices with matrix row operations. Notice we have not used row operations during the calculation of a 2x2 inverse, so, why trying it with a different method when the matrix gets a little bigger?
The reason is that we could use a process to find the inverse of a larger matrix based on the same principle as the one we are using today for a 2x2 matrix (which would also contain a factor of one over the determinant of the matrix), BUT, as the original matrix gets bigger, such process becomes too large and time consuming to be practical. So, we will be looking into a method using row operations because we believe is a much more practical approach.
For now, we will continue to focus on the inverse of 2x2 matrices only, so let us continue.
Exercise problems for finding the inverse of a 2x2 matrix
Example 1
Using the matrices X and Y provided below: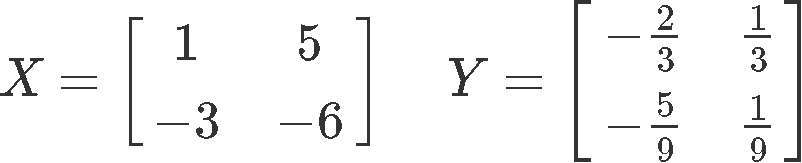
Check if the two matrices are inverses.
We attack this problem by remembering that two matrices are inverses of each other they will produce an identity matrix of their same dimensions when being multiplied, just as described in equation 2 for the case of 2x2 matrices. Therefore, let us use that expression and multiply matrices X and Y in order to see what they produce:
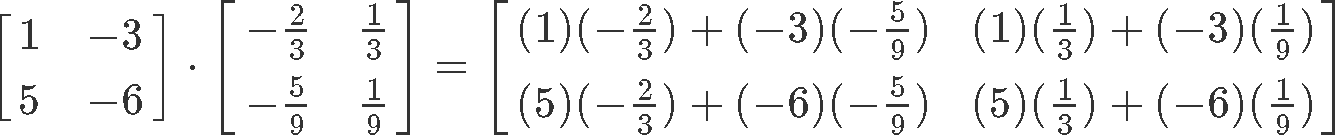
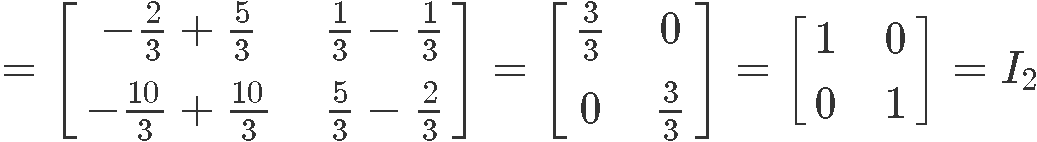
As you can see, the product of matrices X and Y happens to be the identity matrix of second order, therefore, these two matrices are inverses of each other.
Example 2
Just as done in problem example 1, use the two matrices (A and B) defined below and show if they are inverses of each other.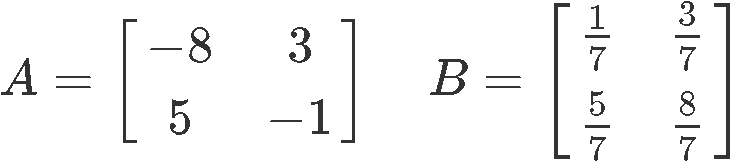
So, we multiply A and B:
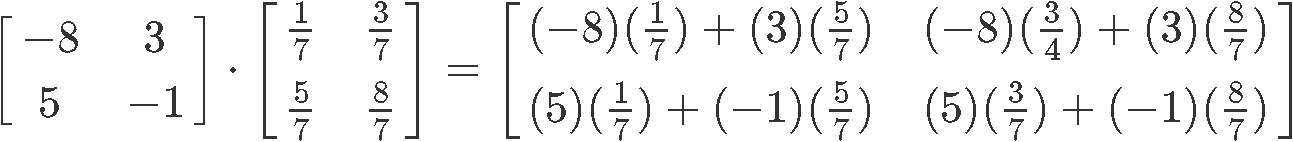

Since the product of A and B is an identity matrix, then that means A and B are two matrices inverses of each other.
Example 3
Once more, we use the matrices A and B provided below: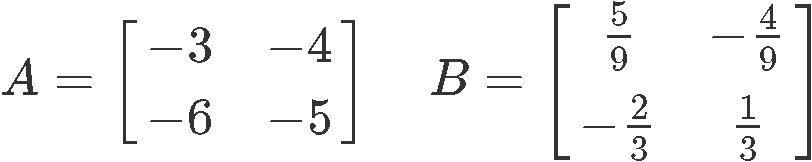
And check if the two matrices are inverses by multiplying them:
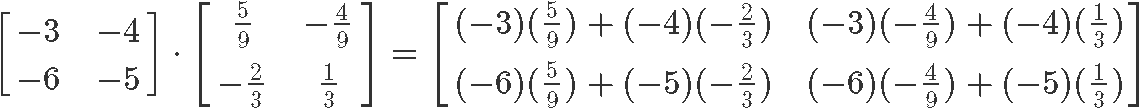
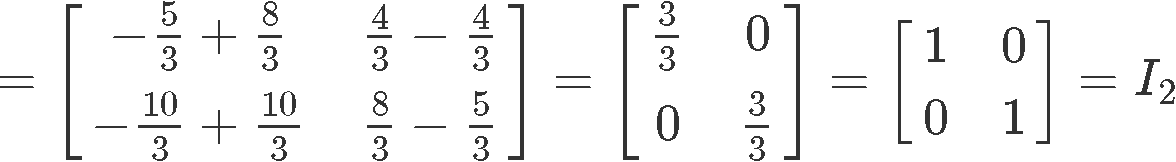
And once more, we have proved that A and B are inverses of each other due the identity matrix being the result of their multiplication.
Now, before we continue with some other exercises, it is important to note something: The order in which you multiply matrices which are inverses of each other does not make a change on their product, their multiplication will still produce the identity matrix.Therefore, if a square matrix is invertible, the matrix multiplication of such matrix and its inverse is commutative (no matter the order in which they are multiplied, they always produce the same result: the identity). You can check this on your own and we recommend that you to do it for practice.
For the next four example exercises we will be using the general formula for inverse of 2x2 matrix as shown in equation 5, in order to obtain the result in each case.
Example 4
Find the inverse of 2x2 matrix X defined below: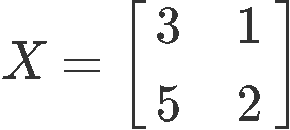
For this, as mentioned before, we use equation 5 (inverse of 2x2 matrix formula) assuming the matrix X follows the element notation from equation 3. Therefore, the computation of the 2x2 inverse matrix goes as follows:
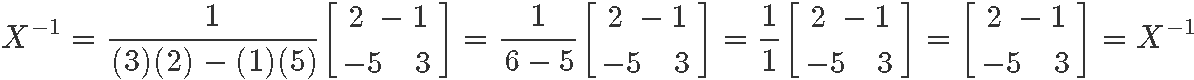
Example 5
Having matrix A as defined below: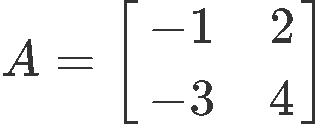
Calculate its 2x2 matrix inverse:
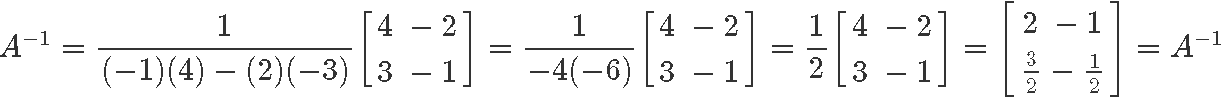
Example 6
Calculate the matrix inverse 2x2 of F, which is defined below: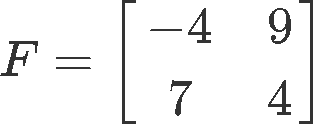
Using equation 5 we obtain:
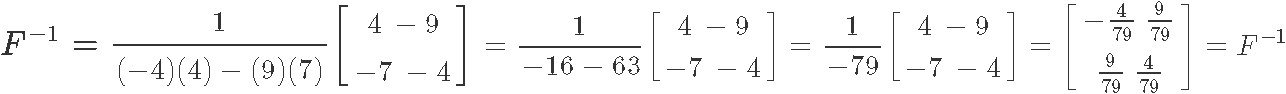
Example 7
If C is defined as the identity matrix of second order (just as shown below). What is the inverse of matrix 2x2 on this case?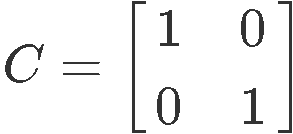
We truly do not need to make any calculations to answer this question since during our lesson on the 2x2 invertible matrix we learnt that the identity matrix is an involutory matrix (or just an involution for simplicity). Remember that an involutory matrix is that which multiplied by itself (squaring the matrix) produces the identity matrix, and so, an involutory matrix is that which is its own inverse. Therefore, we can quickly conclude the inverse of C for this case will be C itself.
We have even proved this before by multiplying the 2x2 identity matrix by itself generating the identity matrix once more, such as shown here:
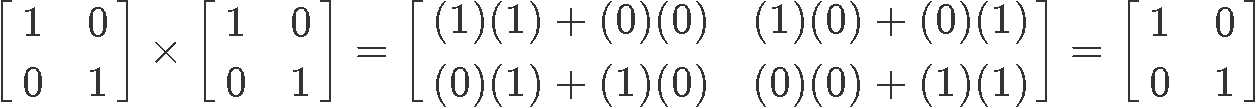
For the purpose of clarity, let us not work the inverse using the formula for the inverse of a matrix 2x2 shown in equation 5 so we can see the same result will be obtained:
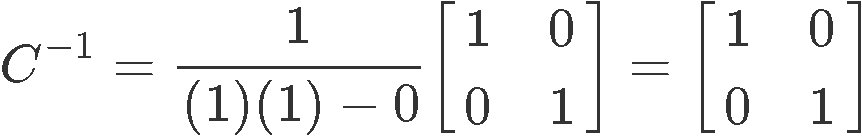
So, as predicted before, the inverse of matrix 2x2 named C is C itself due to involution.
Before we go, let us recommend you an extra resource containing information and extra example exercises about inverse matrices, besides it, you could also visit this handout on the inverse of a matrix and Cramers rule.
So, this is it for today, see you on our next lesson!
Let the matrices X and Y be inverses. Then that means the following is true:
XY=I
where I is the identity matrix. To be more precise, we can say that since X and Y are inverses, then Y is the same as X−1, and so we can say that
XX−1=I
Let Xbe a matrix and you want to find the inverse (denote as X−1 ). Then we use the following formula:
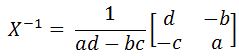
Let Xbe a matrix and you want to find the inverse (denote as X−1 ). Then we use the following formula:
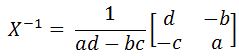
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today

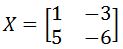 and
and 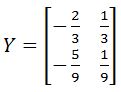 are inverses.
are inverses.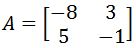 and
and  are inverses.
are inverses. and
and 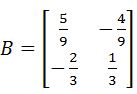 are inverses.
are inverses.