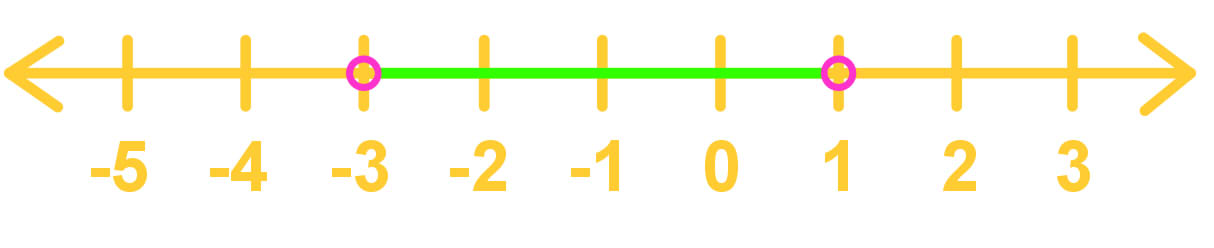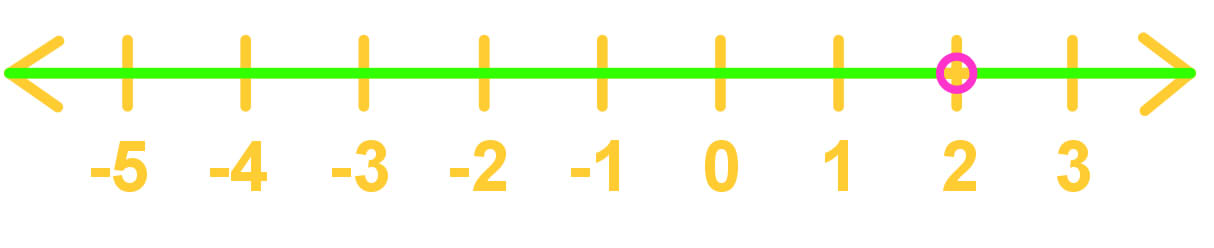Set builder notation
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
0/1
Intros
0/7
Examples
Lessons
- Translating Intervals On Number Lines Into Set Builder Notation Form
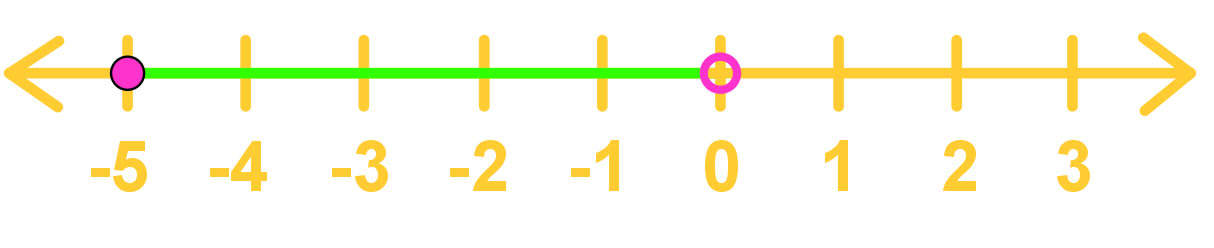
Translate the following intervals into set builder notation form.
- Evaluating the Domains of Expressions in Set Builder Notation Form
What are the domains for the following expressions? Write the answers in set builder notation form.