Distance formula: d=(x2−x1)2+(y2−y1)2
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Distance between two points
If you recall the Pythagorean Theorem, the distance formula is actually a variation of that theorem.
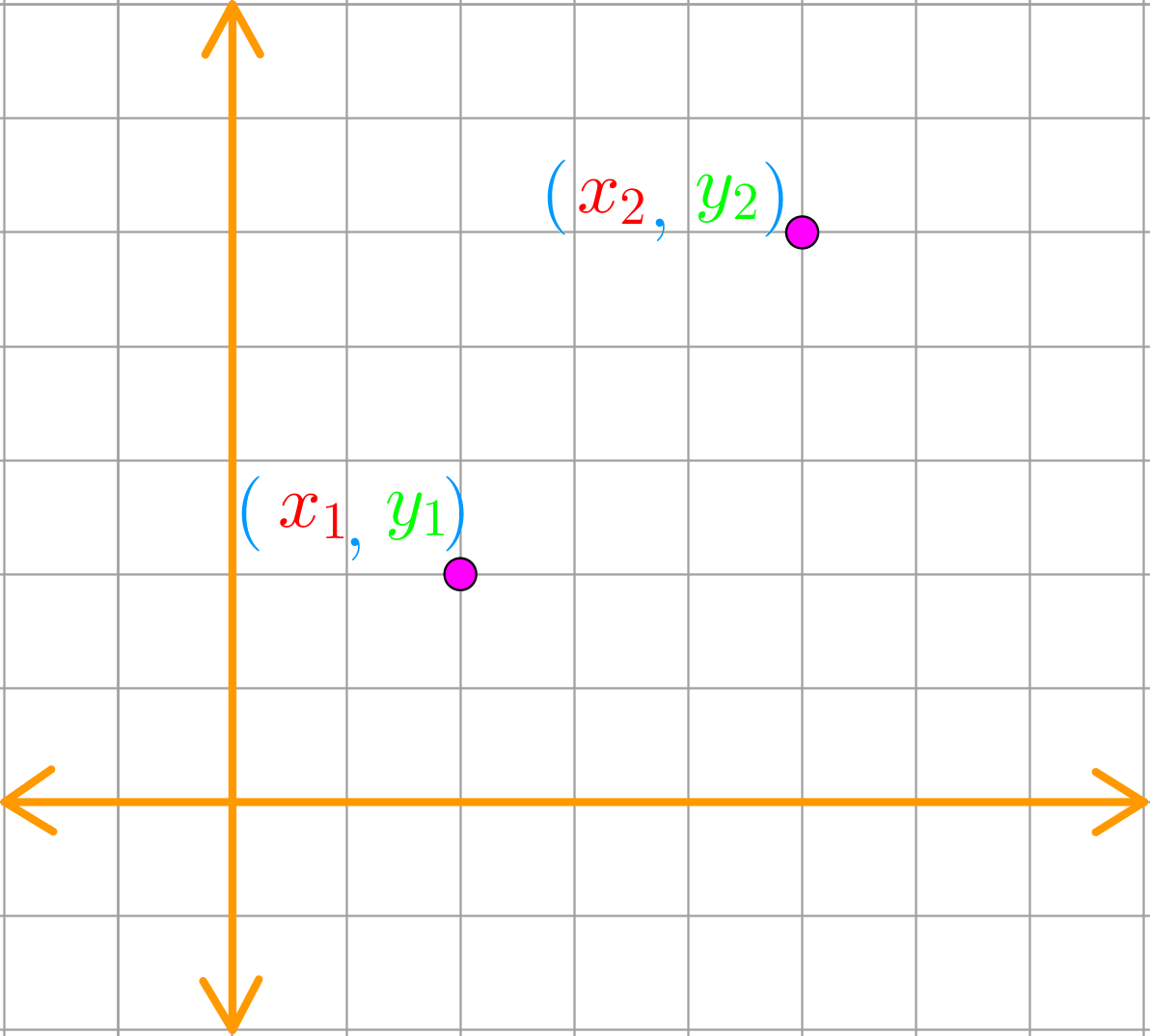
Let's look deeper into this with the points on the above graph. We have two points, one at x1, y1 and another one x2, y2. To calculate the distance between them, join the points together and form a right-angled triangle that uses the two points as its corners.
The lengths of the two sides of the right-angled triangle are easy to find with the help of the x- and y- axis. Simply subtract the x-values and the y-values to find the lengths.
Now that we have the lengths of the two sides of the triangle, do you recall how we find its hypotenuse? We use the formula: c^2 = a^2 + b^2
Therefore, if we were to plug in the points of (x1, y1), and (x2, y2), then move the square over to the other side of the equation so that it becomes a square root, we'll get the formula for distance.
What is the distance formula?
d is used to represent distance in this case. This formula is always true and useful when you've got two points. As long as you know where they are on a graph, you can plot them, then draw a right-angled triangle to help you find the length of its hypotenuse. This makes use of the Pythagorean Theorem which we learned back when studying geometry. The hypotenuse is the distance you're looking for between the two points! Now you've learned how the distance formula works.
Key things to remember when calculating for distance is: 1) Do not mismatch your x and y values. Ensure that you've matched them up properly in the right order, such that if you use a the x-value in point A, match it up with the x-value in point B when doing subtracting. Then for the second part of the formula, make sure you're again using the y-value from point A and then subtracting the y-value from point B. 2) Simplify what is inside the parentheses before carrying out squaring. That's the correct order in doing math problems, and holds true in the distance formula. 3) Remember to write down the square root symbol. It's a good habit to have and if you leave it till the end, you may forget to put it back in and therefore get the wrong answer.
Examples for finding distance
Let's put the formula for distance into use with an example question.
Question: What is the distance between A(4,2) and B(6,8)?
We know that we'll be using both the x-values and the y-values. Simply plug in the numbers into the distance formula. It'll look something like the following:
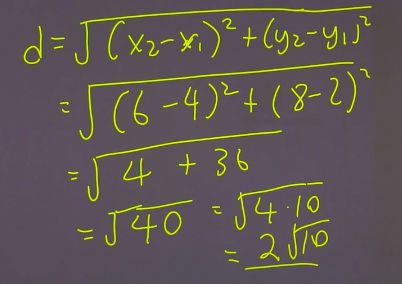
In the above, we consider B as point 2, and consistently use point 2's coordinates before A's in the formula. Don't forget to square the differences between the X's and Y's, and you'll get a number under a square root. Make sure to simplify the answer so that certain numbers can be brought out from the radical symbol.
How about if we were to do horizontal or vertical lines? Would the distance formula work? The short answer is that it will. However, there's an easier way to do this. When dealing with horizontal lines, the length of the line is simply the difference between the two points' x-coordinates. In a similar fashion, a vertical line's length can be found by subtracting one of the y-coordinates with the other. You can feel free to try this out yourself with coordinates from a vertical or horizontal line, and you'll find that you'll get the same answer by just subtracting the coordinates and using the distance formula.
For a recap on the concept, here's a good resource for you to go through. If you wanted to play around with different coordinates and see how the distance formula works, try it out on this interactive chart!
Basic Concepts
remaining today
remaining today



