Solving absolute value equations
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Examples
Lessons
- Solving Equations with One Absolute Value Solve each absolute value equation: i) algebraically ii) verify the solution graphically
- Solving Equations with Two Absolute ValuesSolve each absolute value equation: i) algebraically ii) verify the solution graphically
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Solving Absolute Value Equations
What is Absolute Value?
Before we get into solving equations containing absolute values, we must first have a firm grasp at what "absolute value" actually means. See our article on the absolute value function for more information, as well. Also, before reading further, be sure to refresh your memory on how to solve polynomial equations, solving quadratic equations by factoring, and solving quadratic equations by completing the square.
In the most basic sense, the absolute value of something is simply just the "positive" version of it. Take for example the absolute value of -8, which we express as |-8| (the long bars on either side are the notation for absolute value), in this case, the absolute value of -8 is simply just 8. Again, all we need to do in this case is make -8 positive, and thus we have simply 8. In the case of equations, as we'll see next, the process of evaluating these absolute value expressions is just the same!
Absolute Value Equations:
Now that we understand absolute values and their importance, let's take a closer look at equations with absolute value. Absolute value equations or expressions are evaluated the same way as we did with |-8| above. Let's look at a couple of small examples to make sure we have a good grasp of the concept of absolute value.
i) ∣2x−8∣=2x+8
ii) ∣−48x2+4x−8x3∣=48x2+4x+8x3
As you can see, just like before, all we are doing is making every term in the equation positive. In other words, we are taking the absolute value. This process is the same for all algebraic expressions. However, where things are different – and far more tricky – is when we try solving absolute value equations.
Solving Absolute Value Equations:
Learning how to solve absolute value equations is actually a simple task – all we have to do is practice a bit first! As always, the best way to do so is to take a look at an example problem.
When it comes to solving absolute value equations, there are several methods. The first, and arguably the easiest, is to solve algebraically. We will go over the algebraic technique in this lesson.
Example 1:
Solve the absolute value equation algebraically, and then verify using the absolute value graph.
STEP 1: Express the Absolute Value as a Piecewise Function
Before we solve the equation, it is very important to recognize the tricky difference that occurs when solving absolute value equations – we can't just consider the positive value. Because we are solving the equation, we don't know the value x. The value for x can be positive or negative, and thus we must account for both cases. To accomplish this, we create what is known as a "piecewise" function.
When we express |2x-6| as a piecewise function, we end up with two cases – the negative piece and the positive piece:
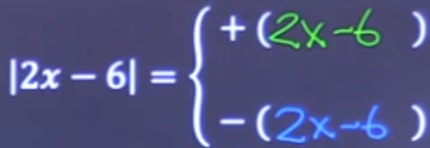
STEP 2: Solve Each Case
Next, all we need to do is make each case equal to the right side of the given equation.
i) Negative Piece:
ii) Positive Piece:
We are then left with x = -1 and x = 5 as potential solutions.
STEP 3: Check The Answer
For our third and final step, all we need to do is check that our above solutions are correct. To do this, there are three main methods. We will go over all of them.
1) Number Line
This first strategy is arguably the most difficult. The latter two are much easier, and are recommended. Nevertheless, we will still go over this method. First, solve for x in our absolute value expression to find out at what point on the function is the vertex.
Thus, our "vertex" is 3. On a number line, this gives us regions on the number line that are x < 3 and x > 3.

In the region x < 3, x can be any number that is smaller than 3 to |2x - 6|. If the result is a negative number, we pick the negative piece in the function. In the region x > 3, x can be any number that is greater than 3 to |2x - 6|. If the result is a positive number, we pick the positive piece in the function.
If we look at our solutions again on this number line, we end up with:

Now, let's evaluate our solutions to see if they are valid.
Negative Piece:
Compare x = -1 to x < 3. -1 < 3 is true. So, we retain the solution.
Positive Piece:
Compare x = 5 to x > 3. 5 > 3 is true. So, we retain the solution.
2) Left Side = Right Side
In this method, all we have to do is plug in our potential solutions of x = -1 and x = 5 into the equation and see if the left side equals the right side. Let's go ahead and try each solution with this technique.
Therefore, x = -1 is a valid solution
Therefore, x = 5 is a valid solution
3) Graphing
For easy-to-graph functions, all we need to do is graph both the left and right equations, and see where they intersect. If they intersect at our solved solutions, our solutions are valid. Below is a graph of this example.
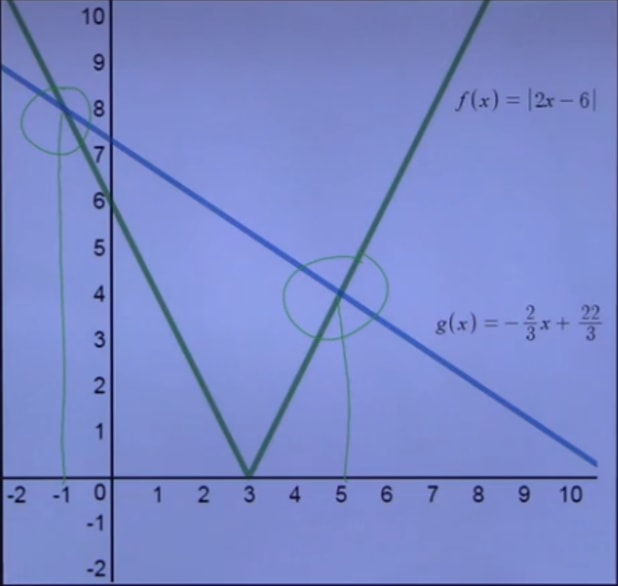
And that's all there is to it! For further, related study, see how articles on how to solve radical equations and solving rational equations. Also, for an excellent tool to check your work, check out this link here.
Basic Concepts
Related Concepts
remaining today
remaining today



