How to simplify radicals
Radicals can be simplified through adding and subtracting, but you should keep in mind that you sometimes can't "cleanly" simplify square roots down into a number. The first thing to note is that radicals can only be added and subtracted if they have the same root number. If the radicals in a question are unlike, you won't be able to combine them together. That's one of the main rules for radicals that you should remember.
How to subtract radicals
Our example will help you grasp the basics of what we mean when we say you have to find like radicals before combining them. The simplifying radicals problem below deals with how to subtract radicals.
Question 1:
Solution:
We are going to first simplify this expression. We will perform a division analysis for the number 90 in order to identify its roots:

We learn that can be re-written as:
Since we are dealing with square roots (which is what a radical sign stands for. There should be a tiny 2 next to the radical sign to indicate that we're working with square roots, but it is generally accepted to simply write the sign without it), we are looking for numbers in pair. In this case, we can see that we have a pair of 3s

Now, we can take the pair outside of the radical (square root), leaving us with:
This means our question can be transformed into the following expression:
You can see that we've now identified the "like" radicals in the question: 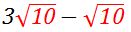 .
.
We can finally do the subtraction, and the result gives us:

As you can see, the number that we ultimately get isn't a clean, whole number, but rather a number followed by a radical. It's best to leave the number like this because if we take the square root of the radical, we'll get a messy decimal number. Unless if the question tells you to, there's no need to simplify it further. You've already got the simplest radical form via this answer.
How to add radicals
In this example, let's take a look to see how to add radicals, as well as deal with a cubic root rather than a square root.
Question 2:
Combine the expression into a single radical.
Solution:
Again, let us first perform a division analysis for and


This allows us to rewrite the original question into this expression:
Since we are dealing with cube root, we are looking for numbers in triplets. In this case, we have a triplet of 2s in 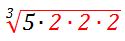 and a triplet of 3s in
and a triplet of 3s in 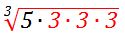
Now, we can take the triplets outside of the radical (cubic root), and get this expression:

Now that the two numbers have the same radical: 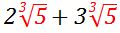 We can do the addition, and the result is:
We can do the addition, and the result is:

Dealing with other roots of varying powers can be tackled in the same way. Just make sure you're combing the same roots, and not, say, a cubic root with a square root when you want to simplify radicals. There are some examples here that illustrate what to do when you have different roots.






